17. Определение предела функции в точке. Основные теоремы о пределах (одну из них доказать). Предел функции в точке

Определение. Число называется пределом функции при стремящемся к (или в точке ), если для любого, даже сколько угодно малого положительного числа , найдется такое положительное число (зависящее от ), что для всех , не равных и удовлетворяющих условию , выполняется неравенство .

Это предел функции обозначается: или при .

Основные теоремы о пределах. Признаки существования предела

Пусть и - функции, для которых существуют пределы при ( ): , .

Сформулируем основные теоремы о пределах:

1. Функция не может иметь более одного предела.

Предположим противное, т.е. что функция имеет 2 предела А и D, . Тогда на основании теоремы о связи бесконечно малых величин с пределами функции: , , где и - бесконечно малые величины при ( ). Вычитая почленно эти равенства, получим: , откуда . Это равенство невозможно, т.к. на основании свойства 1 бесконечно малых это величина бесконечно малая. Следовательно, предположение о существовании второго предела неверно.

2. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.Е.

.

3. Предел произведения конечного числа функций равен произведению пределов этих функций, т.Е.

.

По условию и , следовательно, на основании теоремы о связи бесконечно малых величин с пределами функции: , , где и - бесконечно малые величины при ( ). Перемножая почленно оба равенства, получим:

.

На основании свойств бесконечно малых последние три слагаемые представляют величину, бесконечно малую при ( ).

Итак, функция представляет сумму постоянного числа и бесконечного малой . На основании обратной теоремы о связи бесконечно малых с пределами функции это означает, что .

В частности, постоянный множитель можно выносить за знак предела, т.е.

.

4. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.Е.

, .

5. Если 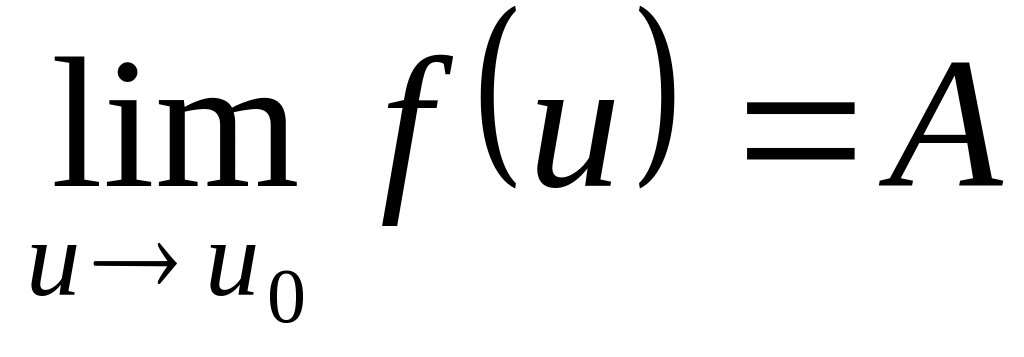, , 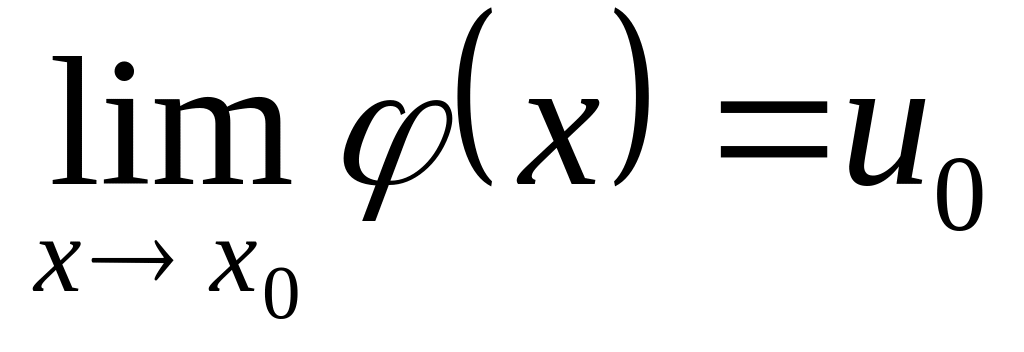то предел сложной функции

.

6. Если в некоторой окрестности точки (или при достаточно больших ) 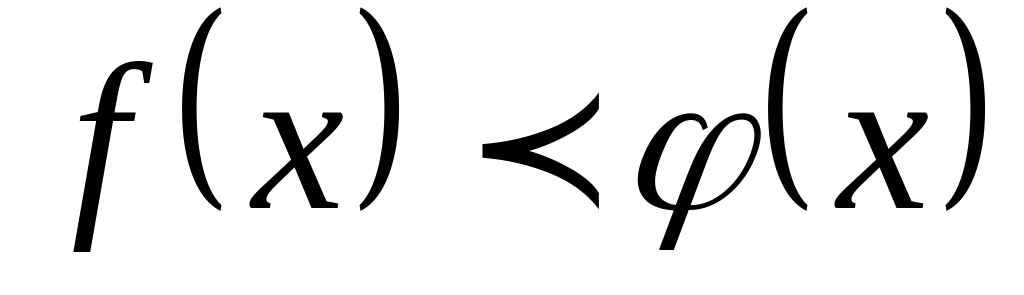, то

.

18. Бесконечно малые величины (определение). Свойства бесконечно малых (одно из них доказать). Бесконечно большие величины, их связь с бесконечно малыми.

Бесконечно малые величины

Определение. Функция называется бесконечно малой величиной при или при , если ее предел равен нулю:

.

Связь бесконечно малых величин с пределами функций

Теорема 1. Если функция имеет при ( ) предел, равный , то ее можно представить в виде суммы этого числа и бесконечно малой при ( ), т.е.

.

Теорема 2. Если функцию можно представить как сумму числа и бесконечно малой при ( ), то число есть предел этой функции при ( ), т.е.

.

Свойства бесконечно малых величин

1. Алгебраическая сумма конечного числа бесконечного малых величин есть величина бесконечно малая.

По условию и - бесконечно малые величины при . Это означает, что для любого найдутся такие числа , что для всех и удовлетворяющих условиям:

и (1.1)

выполняются соответствующие неравенства:

и . (1.2)

Если взять в качестве числа минимальное из чисел и , т.е. , то неравенству будут удовлетворять решения обоих неравенств (1.1) , а, следовательно, одновременно будут верны неравенства (1.2). Складывая почленно неравенства (1.2), получим, что;

.

Используя свойство абсолютных величин, т.е. , придем к более сильному неравенству:

(1.3)

Итак, для любого существует такое , что для всех и удовлетворяющих условию верно неравенство (1.3). А это означает, что функция есть величина бесконечно малая.

2. Произведение бесконечно малой величины на ограниченную функцию (в т.ч. на постоянную, на другую бесконечно малую) есть величина бесконечно малая.

3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

Отношение двух бесконечно малых (неопределенность вида ) в зависимости от характера изменения переменных в числителе и знаменателе может оказаться или числом, или бесконечно малой или бесконечностью.