17.Задача линейного программирования

1. Постановка задачи линейного программирования

Среди известных разделов исследования операций наиболее развитым и законченным является линейное программирование. Решение задачи линейного программирования осуществляется в три этапа:

1. Составление математической модели (постановка задачи);

2. Определение оптимального решения симплекс-методом;

3. Анализ полученного решения.

1.1. Общая форма задачи линейного программирования

Математическую задачу линейного программирования можно представить следующим образом:

«Найти совокупность значений n переменных х₁, х₂, …, х_n, удовлетворяющих системе ограничений:

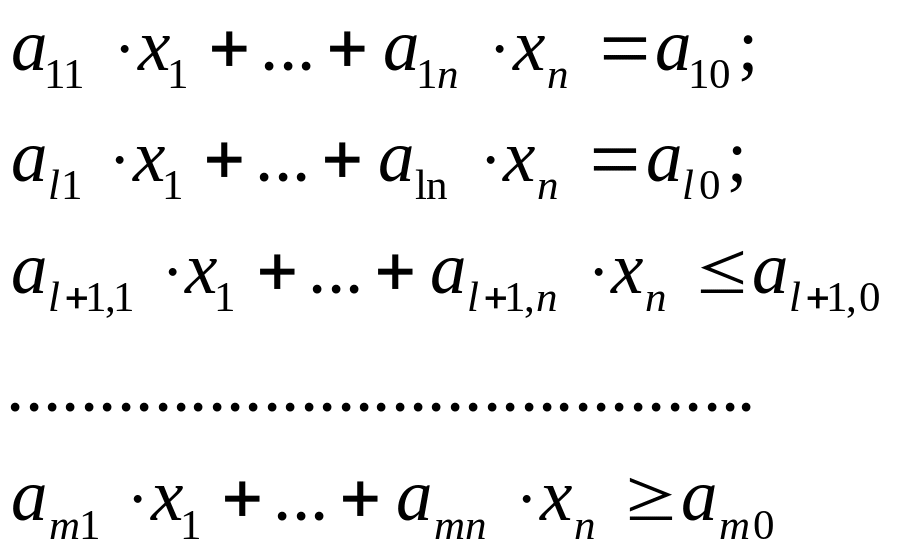
(16.1)

и условием неотрицательности

,(16.2)

где , для которых целевая функция

(16.3)

достигает экстремума (максимума или минимума).»

Определим основные понятия линейного программирования:

Возможное решение (план) – это вектор , координаты которого удовлетворяют системе (1);

Допустимое решение (план) – это вектор , координаты которого удовлетворяют не только системе (16.1), но и условиям неотрицательности (16.2);

Область допустимых решений – это совокупность возможных допустимых решений;

Оптимальное решение – это допустимое решение , для которого линейная функция (16.3) достигает максимума или минимума.

Ограничительные условия (16.1) могут состоять только из уравнений (l=m), только из неравенств (l=0) или из уравнений и неравенств (0lm). В первых двух случаях они называются однородными, в третьем случае – смешанными.

1.2. Каноническая форма задачи линейного программирования

Для единообразия формулировки задачи линейного программирования и удобства применения симплекс-метода вводится следующая каноническая форма:

«Найти совокупность знаний n переменных х_k (где k=1,2,…, n), удовлетворяющих системе m уравнений:

(16.4)

при условии неотрицательности

(где k=1,2,…, 3) (16.5)

для которых целевая функция

(16.6)

достигает максимума».

1.3. Приведение задач линейного программирования к канонической форме

1. если в задаче требуется минимизировать целевую функцию z, то заменив ее на противоположную 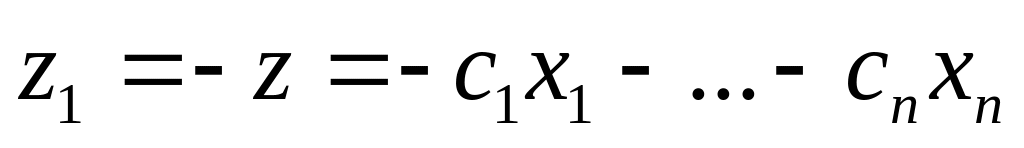, придем к эквивалентной задаче максимизации функции z₁.

2. если условию неотрицательности подчинены не все переменные (tn), то вместо каждой произвольной (т.е. неподчиненной этим условиям) переменной х вводится две неотрицательные переменные и из соотношения .

Пример.

Привести к канонической форме следующую задачу линейного программирования:

« Найти совокупность значений , удовлетворяющих системе ограничений

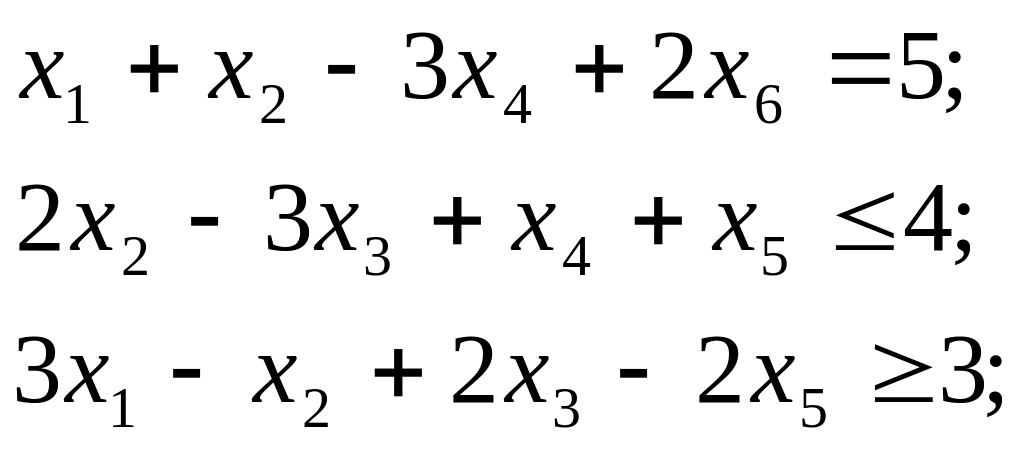
и условиям неотрицательности , для которых целевая функция ».

Для приведения задачи к каноническому виду:

1. введем во второе и третье неравенство балансовые переменные х₇ (со знаком плюс) и х₈ (со знаком минус);

2. т.к. условию неотрицательности не подчинены переменные х₃ и х₄, то введем вместо каждой из них разность двух неотрицательных переменных ; ;

3. при переходе от задачи минимизации к задаче максимизации вместо целевой функции z введем обратную ей функцию z₁=-z, тогда в результате получим каноническую форму:

«Найти совокупность значений десяти переменных , удовлетворяющих системе уравнений:

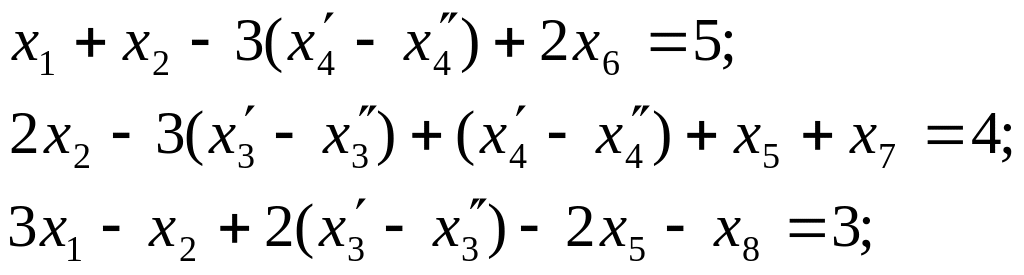
при условии неотрицательности , для которых целевая функция z₁ достигает максимума ».

Сформулированная таким образом задача линейного программирования может решаться стандартным симплекс-методом.