18

f(t) , R(t) и (t) для некоторых законов распределения

4. F(t) , r(t) и (t) для некоторых законов распределения

Рассмотрим функции плотности распределения, вероятности безотказной работы и интенсивности отказов для наиболее распространенных законов распределения наработки на отказ.

4.1. Экспоненциальное распределение

Это распределение очень часто (хотя и не всегда обоснованно) используется для оценки надежности в период нормальной работы изделия (до износа). Как уже отмечалось, отказы в этот период определяются неблагоприятным стечением обстоятельств (внезапные отказы) и не зависят от состояния объекта.

Функция плотности для экспоненциального распределения имеет вид:

f(t) =  exp (-t), t  0.

Иногда вместо  используется 1/, где  - параметр распределения, означающий среднюю наработку на отказ.

Вероятность безотказной работы определяется выражением:

R(t) =exp(-t), t  0.

Интенсивность отказа в этом случае постоянна.

(t) = f(t)/R(t) =  = const.

На рис.4.1 представлен типичный вид графиков рассмотренных функций.

f(t) R(t) (t)

 1 

Рис. 4.1. Графики f(t) , R(t) и (t) для экспоненциального закона

распределения

4.2. Нормальное распределение

Выражение для функции плотности нормального распределения f(t) приведено выше в п. 2.4.1. Вероятность безотказной работы вычисляется по формуле:

= 1 - F(t).

Или, учитывая нормированную форму представления нормального распределения (смотри п. 2.4.3) , R(t) = 1 - F(t) = 1 - Ф(z) = Ф(-z), где z = (t - _t)/S_t .

Интенсивность отказов (t) = f(t)/R(t) для нормального распределения представляет собой монотонно возрастающую функцию.

На рис. 4.2 представлены графики рассмотренных функций для нормализованного нормального распределения.( Напомним, что нормализованное нормальное распределение имеет нулевое математическое ожидание и равное единице среднеквадратическое отклонение.

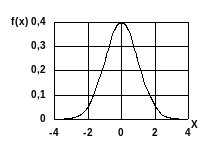
а) б) в)

Рис. 4.2. Графики а) плотности вероятности, б) вероятности безотказной работы

и в) интенсивности отказов для нормального распределения с =0 и S =1.

Пример 4.1. Объект имеет нормальное распределение наработки до отказа с параметрами:  = 30 000 км и S =3 000 км. Определить  при наработке 24 000 км.

Решение.

, где z = (t - _z)/S = (24 000 - 30 000)/3000 = -2.0, тогда, используя табличные значения для нормированных значений f(z) и R(z) = Ф(-z), получим решение путем следующих вычислений

(24 000) = 0,05399/(3000 ^х 0,97725) = 0,184 ^х 10^-4 отказов / км.

4.3. Логарифмически нормальное распределение

Плотность такого распределения описывается следующей функцией

,

где t  0 - наработка на отказ;  и S - параметры распределения (не являющиеся математическим ожиданием и стандартом случайной величины t) причем S > 0, а   <  < .

Если случайная величина x определятся как x = ln t , где t - логарифмически нормально распределенная случайная величина, то x будет иметь нормальный закон распределения с математическим ожиданием  и стандартным отклонением S ,т.е.

E(x) = E(lnt) = ;

V(x) = V(lnt) = S².

В свою очередь (учитывая, что t = exp(x)) математическое ожидание и стандарт для t связаны с  и S следующими соотношениями.

E(t) = _t = exp( + S²/2);

.

Функция логарифмически нормального распределения F(t), а через нее вероятность безотказной работы R(t), могут быть вычислены с помощью функции Ф(z) нормированной случайной величины z, распределенной по нормальному закону

R(t) = 1 - F(t) =1 - Ф[(lnt - )/S] = Ф[ - (lnt - )/S].

Очевидно, что z в данном случае следует определять по формуле

z = (lnt - )/S.

Формула для определения интенсивности отказов имеет следующий вид:

,

где (z) - нормированная функция плотности нормального распределения.

Графики функций плотности распределения для различных значений параметров  и S=1 представлены на рис. 4.3.

Рис. 4.3. Логарифмически нормальное распределение

Пример 4.2. Наработка на отказ некоторого изделия имеет логарифмически нормальное распределение с параметрами =5 и S=1. Требуется найти вероятность безотказной работы и интенсивность при наработке 120 тыс. км.

Решение. Определяем значение аргумента для нормированного нормального распределения и затем используем табличное значение функции распределения для определения вероятности безотказной работы:

z = (lnt – )/S=(ln 120 - 5)/1= - 0,21, R(120)= Ф(0,21)= 0,583.

Интенсивность отказов определится следующим образом:

(t)=(z)/tSR(t)= (-0,21)/120^.1^. 0,583=0,39/120^.1^.0,583=0,0056 отказов/ тыс.км.

Логарифмически нормальное распределение используют для описания процессов восстановления, износовых отказов, отказов от усталости материалов.