Свойства функции Гаусса.
График плотности нормального распределения называют нормальной кривой Гаусса.
Исследуем поведение функции плотности вероятности .
Очевидно, что функция определена на всей оси .
Функция принимает лишь положительные значения, т.е. нормальная кривая расположена над осью
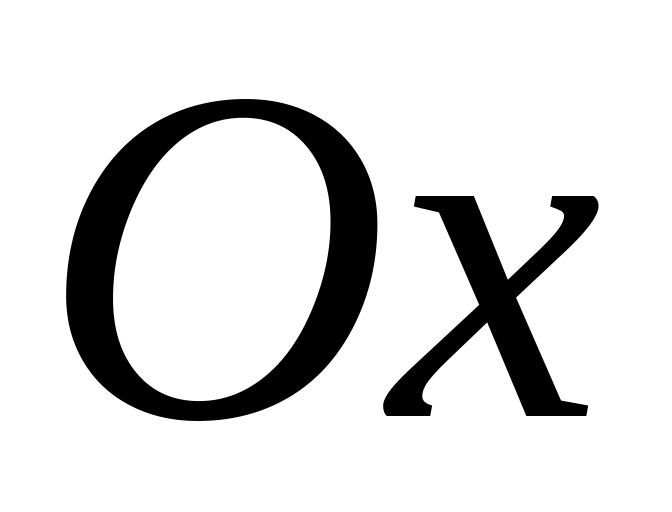.Ось служит горизонтальной асимптотой графика. Других асимптот у графика нет.
При
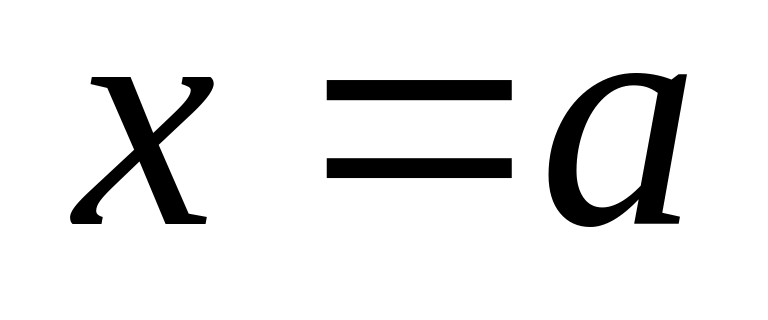функция имеет максимум, равный
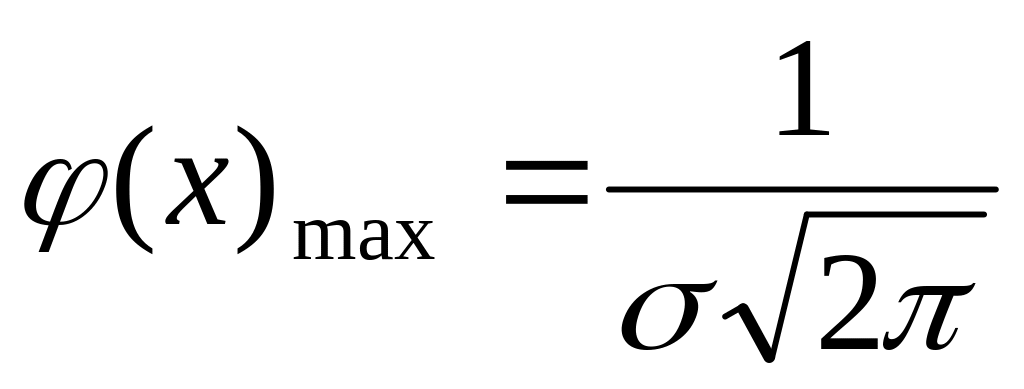
Функция четная: ее график симметричен относительно прямой
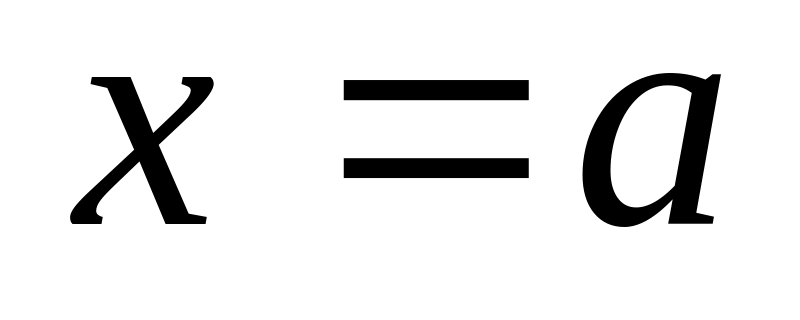
При
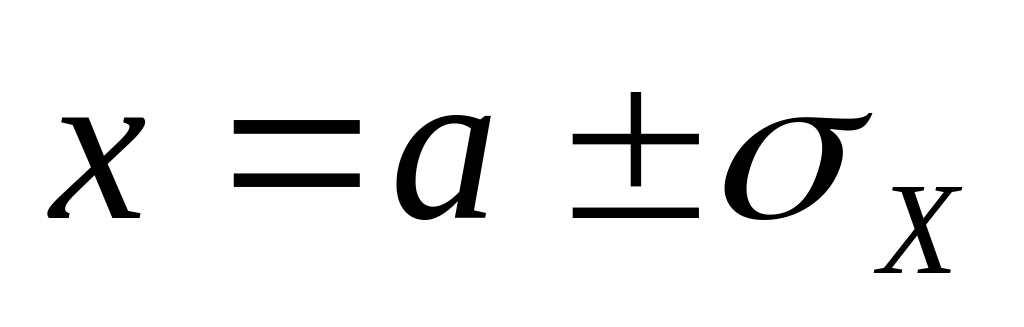график функции имеет точки перегиба.
При
любых значениях
параметров
и
,
площадь, ограниченная нормальной кривой
и осью
равна единице.
Вероятность попадания нормальной случайной величины в заданный интервал.
Часто требуется определить вероятность попадания случайной величины в заданный интервал. Эта вероятность может быть выражена в виде разности функции распределения вероятности в граничных точках этого интервала:
.
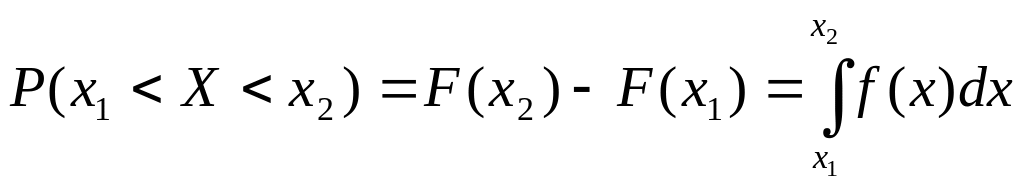В случае нормального распределения
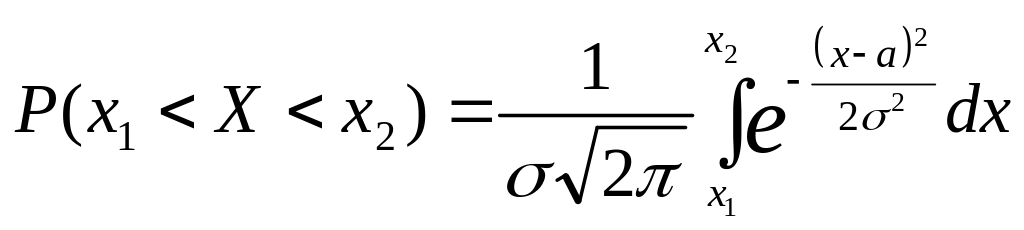
Используя
замену переменной:
,
,
,
получим
,
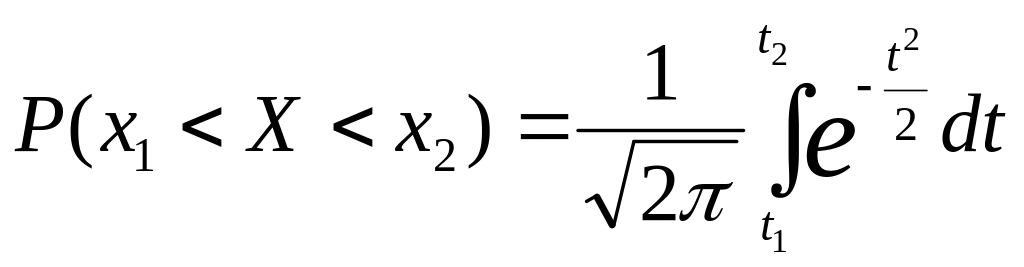где
,
.
Разобьем полученный интеграл на два:
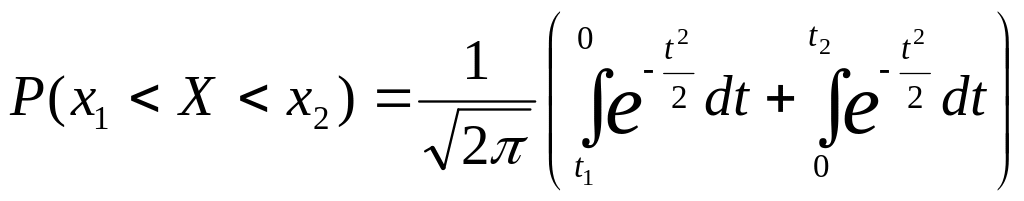
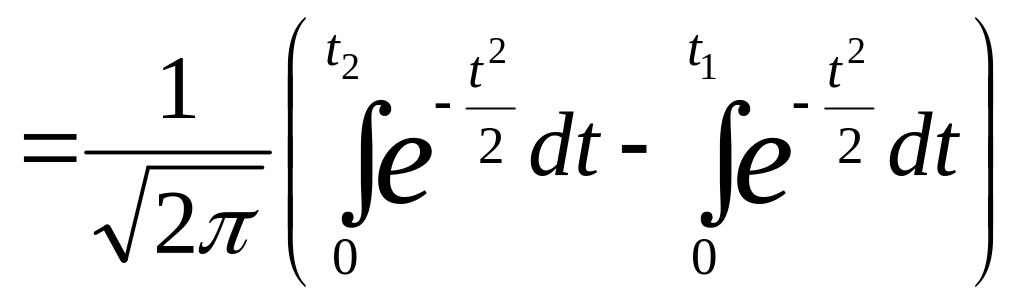
Тогда искомая вероятность может быть выражена в виде:
где
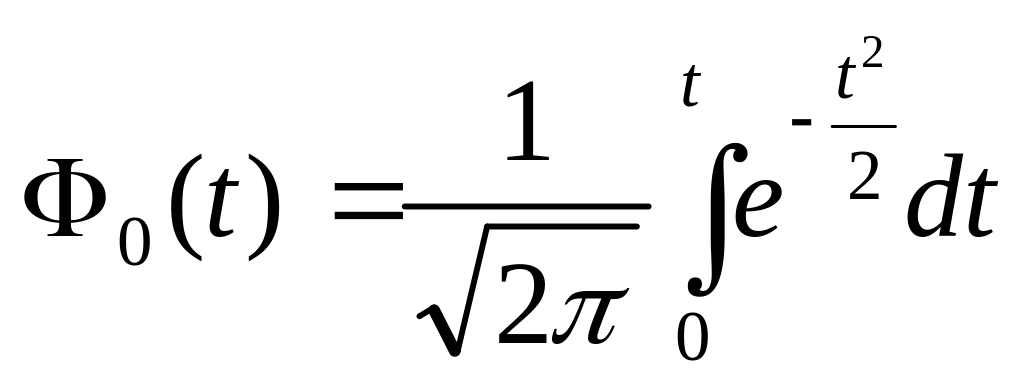- функция Лапласа.
Функция Лапласа протабулирована, что существенно упрощает расчет попадания нормально распределенной случайной величины в любой заданный интервал.
Функция Лапласа и ее свойства.
Функция Лапласа не выражается через элементарные функции:
.
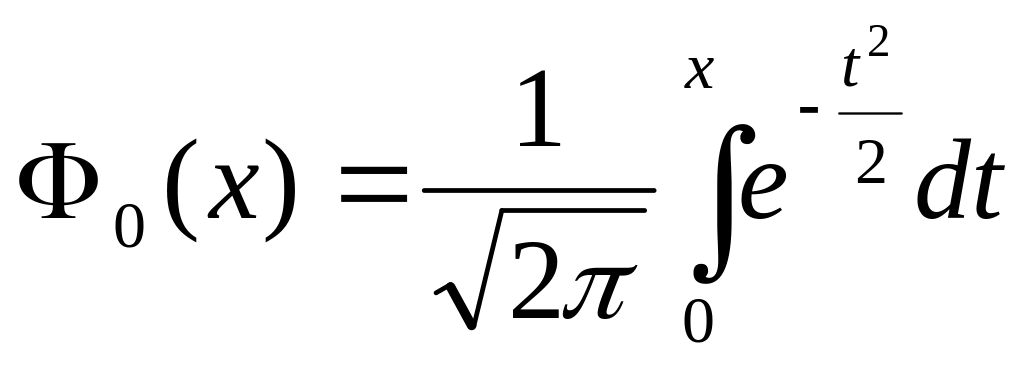Для ее вычисления используются специальные таблицы или методы приближенного вычисления.
Функция обладает следующими свойствами:
;
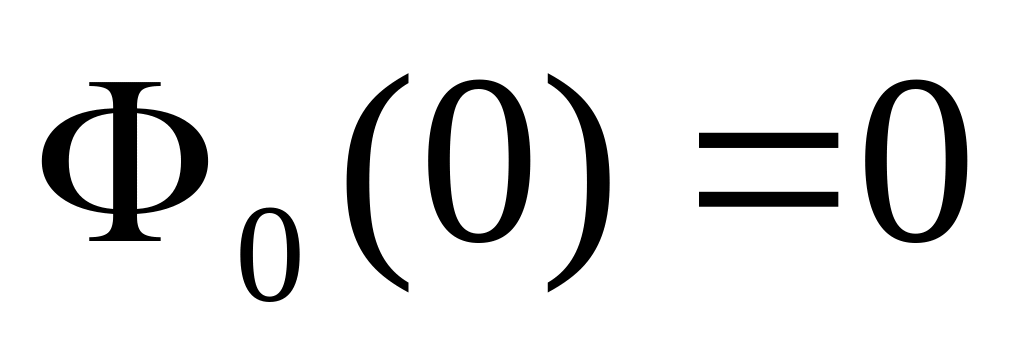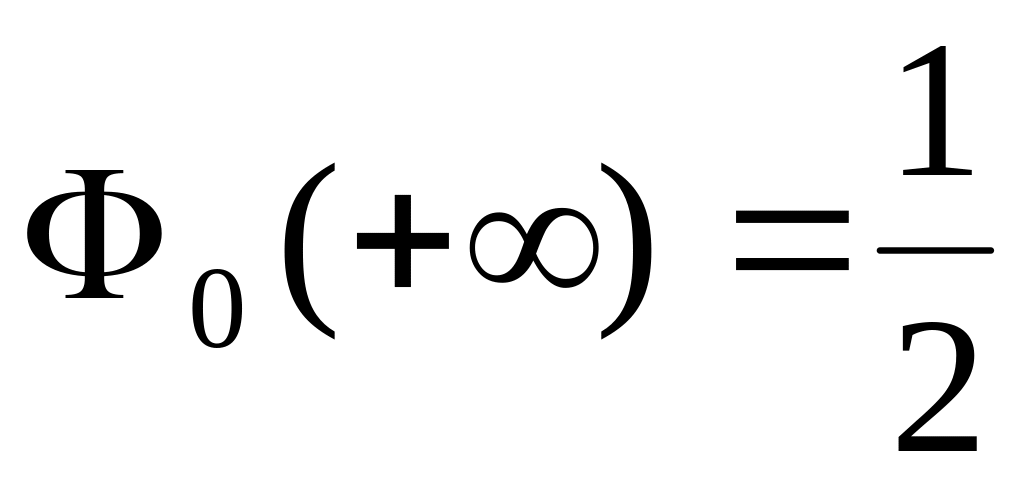;функция – нечетная, т.е.
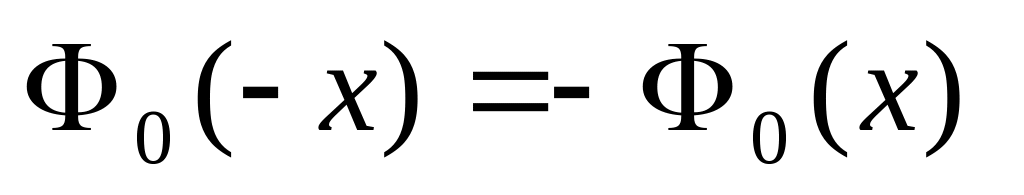, поэтому в таблицах обычно приводятся
значения
только для положительных
;функция – монотонно возрастающая функция ( это следует из того, что
).
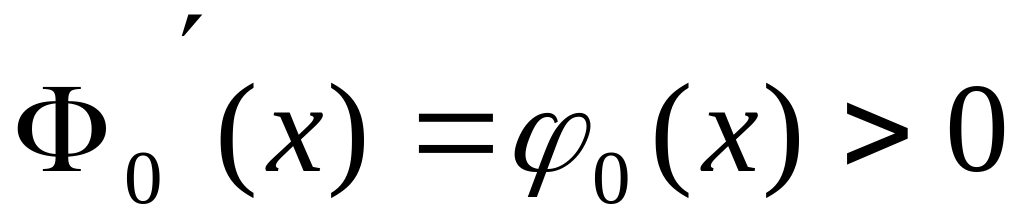О тклонение нормальной случайной величины от ее математического ожидания. Правило «трех сигм».
Часто
требуется вычислить вероятность того,
что отклонение нормально распределенной
случайной величины
по абсолютной величине от математического
ожидания меньше заданного положительного
числа
,
т.е. требуется найти вероятность того,
что выполняется неравенство
.
Заменим это неравенство равносильным ему двойным неравенством
.
Воспользуемся формулой:
Получим:
Если в качестве взять утроенное значение среднего квадратического отклонения , то получим:
,
Таким образом, вероятность того, что абсолютная величина отклонения превысит (утроенное среднее квадратическое отклонение, очень мала 0,0027 или 0,27%). Такие события можно считать практически невозможными.
Другими словами, если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратичного отклонения. В этом и состоит сущность правила «трех сигм».
На практике правило «трех сигм» применяют так: если распределение изучаемой случайной величины неизвестно, но правило «трех сигм» выполняется, то есть основания полагать, что изучаемая величина распределена нормально, и наоборот.
Пример 1. Текущая цена ценной бумаги представляет собой нормально распределенную случайную величину со средним 100 у.е. и дисперсией 9. Найти вероятность того, что цена актива будет находиться в пределах от 91 до 109 у.е.
Решение.
Так как
,
то
Пример 2.
Магазин продает мужские костюмы. По данным статистики известно, что распределение по размерам является нормальным с математическим ожиданием и средним квадратическим отклонением, равными 48 и 2 соответственно.
Определить процент спроса на 50-й размер, при условии разброса значений этой величины в интервале (49,51).
Решение
По условию, a=48, = 2, = 49, =51. Используя формулу
получаем, что вероятность спроса на 50-й размер в заданном интервале равна
Вывод: спрос на 50-й размер составит примерно 24% и магазину нужно предусмотреть это в общем объеме закупки.