1. Случайные события и действия над ними.

Событием называется любой факт, который в результате опыта может произойти или не произойти.

Достоверным называется событие Ω, которое происходит в каждом опыте.

Невозможным называется событие , которое в результате опыта произойти не может.

Возможные события, порождаемые комплексом условий, называются элементарными, если:

а) они различны (т.е. осуществление одного означает неосуществление любого другого);

б) после выполнения комплекса условия обязательно происходит одно из них.

Обозначим через Ω ={ω1, ω2 , ..., ω n , ...} пространство элементарных событий.

Любое объединение элементарных событий называется случайным событием, BΩ.

Событие B осуществляется тогда, когда происходит одно из элементарных событий ωB . В этом смысле пространство Ω может рассматриваться тоже как событие.

Противоположным событию A называется такое событие 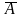, которое заключается в том, что событие A не происходит (A =; A =).

События A_k (k = 1, 2, ..., n) образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие.

Операции:

1.Суммой (объединением) двух событий A и B (обозначается A+B, AB) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.

2.Произведением (пересечением) двух событий A и B (обозначается AB, A∩B) называется такое событие, которое заключается в том, что оба события A и B происходят вместе (совместно).

3.Если событие А, пересеченное с событием В пусто, то мы говорим, что событие А и В несовместимы. Частные случаи: A=; A=A; A=; A=A.

4. Событие А влечет за собой событие В (AB), если всякий раз когда наступает событие А, наступает событие В (А – подмножество (подсобытие) В).

Описанию случайных событий: множества, получающегося объединением элементарных событий. В связи с этим для определения соотношений между случайными событиями в теории вероятностей принят язык теории множеств (табл.1). Для анализа соотношений между случайными событиями могут оказаться полезными следующие соотношения.

1. AB = BA, AB = BA.

Эти равенства следуют из определений.

2.

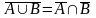
Доказательство следует из следующей цепочки импликаций:

ω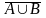 =>ωAB=>ωA, ωB=>ω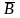 ,ω =>ω  .

и наоборот

ω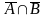 =>ωA,ωB=>ωAB=>ω .

3. .

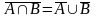4. AB=>  .

Это следует из того, что если ω , то ωB , поэтому ωA и, значит, ω .

Из соотношений 2 – 4 следует, что если задана некоторая конструкция из событий, ее дополнение можно выразить, заменив в ней все события на противоположные, символы объединения, пересечения и включения на символы пересечения, объединения и обратный к включению соответственно. Это свойство известно под названием закона де Моргана, например,

.

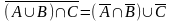2. Алгебра событий.

Поле событий (алгебра событий) – множество событий.

Пусть имеется:  - достоверное событие;  - невозможное событие; A₁, A₂,…,A_n – случайные события; А, В – случайные события и F – поле событий (алгебра событий).

Полем событий F называется совокупность событий, которая обладает следующими св-вами:

1. в эту совокупность обязательно входит достоверное событие: F.

2. если AF, то F.

3. если А,ВF, то ABF; ABF.

A₁A₂…A_nF; A₁A₂…A_nF/.

4. если взять n=, то

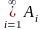(*){A₁A₂…A_n…= ; A₁A₂…A_n…=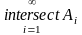

Если (*)F => σ-алгебра. Выделяются 2 понятия: 1. просто алгебра – когда выполняется 3; 2. σ-алгебра – когда выполняется 4.