14. Определение линейных скоростей и ускорений при движении тела около неподвижной точки.

Тело с одной неподвижной точкой можно переместить из одного положения в другое поворотом вокруг некоторой оси, проходящей через не­подвижную точку . Это утверждение – есть теорема Даламбера-Эйлера.

  Конечно, такое перемещение не яв­ля­ется истинным движением тела. На самом деле тело переходило из первого положе­ния в другое каким-то другим, наверное бо­лее сложным путём. Но, если время такого пере­хода мало, то это перемещение будет близко к действительному. А при можно предположить, что для данного момента времени тело поворачива­ется вокруг некоторой оси Р, проходя­щей через неподвижную точку , вращаясь вокруг неё с угловой скоро­стью . Конечно, для каждого дру­гого момента времени эта ось рас­поло­жена иначе. Поэтому ось называют мгновенной осью вращения, а угло­вую скорость – мгновенной угловой скоростью, вектор которой на­прав­лен по оси.

 

Скорость точек тела.

По теореме Даламбера-Эйлера за малое время движение тела можно представить как вращение вокруг неподвижной оси с некоторой угловой скоростью (рис.23).

Рис.23

 Тогда скорость точки : В пределе, при , угловая скорость будет приближаться к мгновенной угловой скорости , направленной по мгновенной оси вращения , а скорость точки - к истинному значению:

.

Но таким же образом находится скорость точки при вращении тела вокруг оси, по которой направлен вектор , в нашем случае – по мгновенной оси вращения . Поэтому скорость точки можно определить как скорость её при вращении тела вокруг мгновенной оси . Величина скорости (рис.23).

 Определение скоростей то­чек тела значительно упроща­ется, если извест­на мгновенная ось вращения . Иногда её можно найти, если уда­стся обна­ружить у тела хотя бы ещё одну точку, кроме , скорость кото­рой в данный момент равна нулю, и провести ось из не­подвижной точки О через эту точку. Так как мгновенная ось вращения – геометрическое ме­сто точек, скорости которых равны нулю в данный момент времени.

Ускорение точек тела.

Сначала определим угловое ускорение тела . При движении тела вектор угловой скорости изменяется и по величине, и по направлению. Точка распо­ложен­ная на его конце будет двигаться по некоторой траектории со скоростью (рис.25).

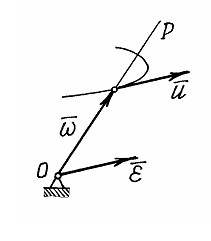
Рис.25

 Если рас­сматривать вектор как ра­диус-вектор этой точки, то .

Итак. Угловое ускорение тела можно опреде­лить как скорость точки, расположенной на конце вектора угловой скорости:

.

Этот результат называется теоремой Резаля.

Теперь обратимся к определению ускорения точек. Ускорение какой-либо точки тела

,

есть сумма двух векторов.

Первый вектор . Модуль его , где h1 – расстояние от точки до вектора . Направлен он перпендику­лярно и . Но таким же способом определяет­ся касательное ускорение. Поэтому первую состав­ляющую ускорения определяют как ка­сательное ускорение, предпола­гая, что тело вращается вокруг оси, совпадающей с векто­ром . И обо­значается этот вектор ускорения так

Второй вектор Модуль его , но , т.к. векторы и перпендикулярны друг другу.

Рис.26

 

Значит , где h2 – расстояние от точки М до мгновенной оси , до вектора .

Направлен вектор перпендикулярно и , т.е. так же как вектор нормального ускорения при вращении вокруг оси , или вектора . Поэтому этот вектор ускорения и обозначают, соответственно, так:

Итак, ускорение точек тела, вращающегося вокруг неподвижной точки, определяется как сумма двух ускорений:

Этот результат называется теоремой Ривальса.

Заметим, что в общем случае векторы и не совпадают и угол между и не равен , векторы не перпендикулярны друг другу, как это было при вращении тела вокруг неподвижной оси.

Динамика