Кинематика
1.Определение скоростей и ускорений точки при различных способах задания движения
Способы задания движения:
Векторный способ: положение точки можно определить, задав ее радиус вектор. r=r(t). Годограф – геометрическое место концов вектора. В декартовых коордr=xi+yj+zk;
V=limt->0(∆r/∆t)=dr/dt; a=d2r/dt2;
Координатный способ. Положение точки определяется декартовыми координатами x, y, z --- x=f1(t), y=f2(t), z=f3(t)
Vx=dx/dt; ax=dvx/dt; v=√vx2+vy2+vz2
Естественный (траекторный) способ: (траектория, начало отсчета известны) s=f(t); v=lim (∆s/∆t); угол между касательными к кривой в двух точках – угол смежности. Кривизна k=1/ρ=ε/ds ->
an=vεds/dsdt=v2/ρ; aτ=dv/dt
2. Кинематические характеристики поступательного и вращательного движения твердого тела.
Поступательное движение:
Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему начальному направлению.
При поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.
При поступательном движении тела траектории его точек могут быть любыми кривыми линиями.
Вращательное движение:
Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными.
Проходящая через неподвижные точки прямая называется осью вращения.
Числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени.
Угловое ускорение характеризует изменение с течением времени угловой скорости тела. Числовое значение углового ускорения тела в данный момент времени равно первой производной от угловой скорости по времени.
3. Определение линейных скоростей и ускорений вращающегося тела в векторной форме.
Числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения. V=ds/dt=h*dφ/dt=hω; направлена скорость по касательной к описываемой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку. из этого следует ускорение: an=vεds/dsdt=v2/ ρ=
=v2/ h=ω2h2/h= ω2h; aτ=dv/dt=h*dω/dt=hε. Тангенциальное ускорение направлено по касательной к траектории, нормальное – по радиусу к оси вращения. a=h√ω2+ε2; отклонение вектора полного ускорения орадиуса описываемой окружности определяется углом tgϻ=ε/ ω2
Длявекторов: |v|=| ω |h=| ω |*r*sinα =| ωxr| (формулаЭйлера); a=( εxr ) + ( ωxv );
Вектор (εxr) направлен как и вектор (ωxr) по касательной к траектории точки, а ( ωxv ) по нормали к траектории.
4. Определение скоростей точек тела при плоскопараллельном движении. Теорема о проекциях векторов скоростей концов отрезка на его направление.
Аналитический метод
При использовании аналитического метода считаются известными уравнения движения плоской фигуры (тела, совершающего плоскопараллельное движение):
Тогда координаты точки М будут
где b – расстояние от точки М до полюса А.
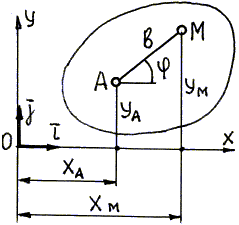
Модуль
скорости точки М определяется по
формуле:
.
Направление
вектора
определяется по направляющим косинусам:
Таким образом, задача по определению скоростей точек плоской фигуры сводится к известному решению соответствующей задачи кинематики точки.
Угловая скорость плоской фигуры определяется дифференцированием последнего уравнения из (54), т.е.
Аналитический метод решения задачи рекомендуется использовать в тех случаях, когда требуется определить скорости точек для большого числа положений плоской фигуры.
Метод, основанный на использовании векторного уравнения.
Скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и скорости этой точки при вращении фигуры вокруг полюса, т.е.
,
где
;
– скорость точки М при вращении плоской
фигуры вокруг полюса А.
Скорость направлена перпендикулярно прямой АМ в сторону вращения фигуры (рис. 25) и равна по модулю
,
где
– угловая скорость вращения плоской
фигуры.
Чтобы можно было определить скорость точки М, используя уравнение необходимо знать скорость полюса А и угловую скорость вращения плоской фигуры . Для решения задачи надо построить параллелограмм скоростей.
Диагональ этого параллелограмма есть искомая скорость точки , ее модуль:
.
Решение задачи рекомендуется начинать с изображения плоской фигуры в положении, соответствующем данному моменту времени. Затем следует выбрать полюс и для заданной точки М записать векторное уравнение. За полюс следует взять точку тела, скорость которой задана. Далее необходимо построить параллелограмм скоростей , вычислить модуль скорости VМ/А , а затем модуль скорости точки VМ.
Теорема о проекциях скоростей двух точек тела:
Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу.
Рассмотрим
какие-нибудь две точки А и В плоской
фигуры (или тела). Принимая точку А за
полюс (рис.32), получаем
.
Отсюда, проектируя обе части равенства
на ось, направленную по АВ, и учитывая,
что вектор
перпендикулярен АВ, находим
и
теорема доказана.