5. Классификация случайных величин.

Классификация случайных величин проводится по специфическим свойствам и функциям распределения.

1) дискретные случайные величины.

В этом случае множество значений 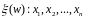конечно либо счетно. 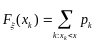. Функция распределения дискретной случайной величины обладает специфическими свойствами:

• она имеет конечное или счетное множество точек разрыва первого рода;

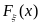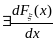• если точка х – точка непрерывности функции распределения , то и .

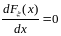Пример дискретной случайной величины:

• случайная величина Бернулл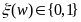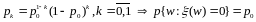и , и ;

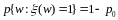• биномиальная случайная величина ;

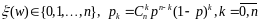• случайная величина Пуассона

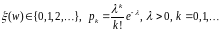
• геометрическая случайная величина

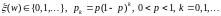
2) Непрерывные случайные величины.

Для функций распределения непрерывных случайных величин имеет место следующее соотношение: (*).

Определение. Функция 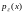из (*) называется плотностью распределения вероятности случайной величины .

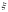В точках существования производной 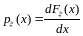плотность обладает следующими свойствами:

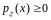1. , т.к. есть производная неубывающей функции;

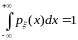2. условие нормировки для плотностей: , т.к. ;

3. .

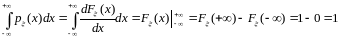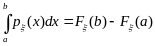Рассмотрим примеры непрерывных случайных величин:

1. случайная величина имеет равномерное распределение, если 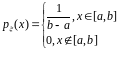. Следовательно, .

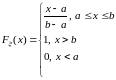2. Случайная величина имеет нормальное (распределение Гаусса), если 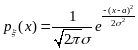, где а – среднее значение случайной величины, - среднее квадратичное отклонение случайной величины.

Если 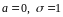, то случайна величина называется стандартной нормированной случайной величиной и пишут .

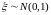3. случайная величина имеет экспоненциальное распределение, если

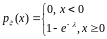
4. распределение Коши

.

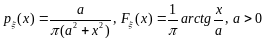6. Математическое ожидание и его свойства.

Пусть имеется случайная величина , заданная на вероятностном пространстве 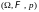. Математическое ожидание характеризует среднее значение случайной величины

Если - дискретная случайная величина , то 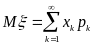, где 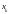- значения дискретной случайной величины, 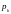- соответствующая им вероятность.

Если 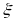- непрерывная случайная величина , то 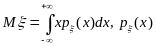- плотность распределения случайной величины .

Рассмотрим свойства математического ожидания:

1) если 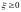, то

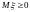
2) 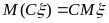, где С – некоторая константа

3) если

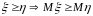
4)

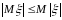
5) введем случайную величину 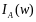, А – некоторое множество. 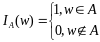называется индикатором события А.

6) если две случайные величины и – независимые случайные величины, то .

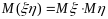Определение. Независимыми называются такие случайные величины и , для которых совместная функция распределения .

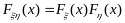Если и – непрерывные случайные величины и являются независимыми, то .

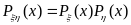7)

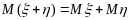
8) пусть 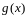- некоторая измеримая функция. Рассмотрим случайную величину 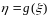, тогда .

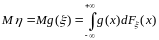9) пусть - многомерная случайная величина, т.е. 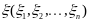, , 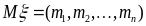где каждая компонента этого вектора .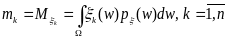

7. Дисперсия и ее свойства.

Определение: Дисперсия СВ 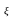называется центральным моментом случайной величины 2-го порядка . Дисперсия СВ - это разброс значений СВ от своего среднего.

Определение: Среднее квадратичное отклонение СВ называется величина .

Для дисперсии случайной величины справедливо следующее равенство: .

Доказательство:

.
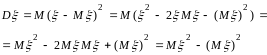