Проекция вектора на ось

Прямая с заданной на ней точкой и единичным базисным вектором называется осью.

Ортогональной проекцией точки A на ось называется точ-ка пересечения оси с перпендикулярной к ней плоскостью, про-ходящей через точку А.

Пусть в пространстве задана направленная прямая l. Проекцией точки М на ось l называется основание перпендикуляра , опущенного из точки М на ось. Если точка М лежит на оси l, то проекция точки М на ось совпадает с М (рис. 4.4).

Рис. 4.4

Пусть – произвольный вектор. Проекцией вектора на ось l называется координата вектора относительно еди-ничного вектора оси, где А₁ и В₁ – проекции точек A и B на ось l, то есть если , то число l называется проекцией вектора на ось l в направлении . Обозначение для проекции:

Из правил сложения векторов и умножения векторов на чис-ло, заданных своими координатами, следует, что:

, где .

Легко показать, что , где j – угол между векторами и , отсчитываемый по правилам три-гонометрии: от вектора против часовой стрелки до вектора .

Следует помнить: проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол прямой.

Разложение вектора по ортам координатных осей

Рассмотрим в пространстве прямоугольную систему координат Oxyz (рис. 4.5). Выделим на координатных осях Ox, Оу и Oz единичные векторы (орты), обозначаемые , , соответственно. Выберем произвольный вектор пространства и совместим его начало с началом координат: .

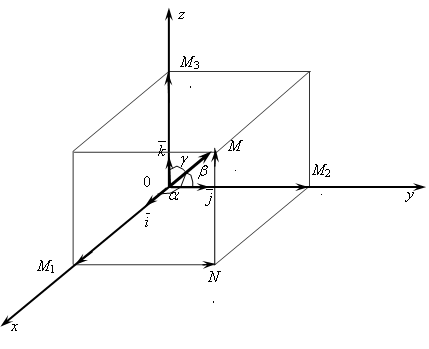
Рис. 4.5

Найдем проекции вектора на координатные оси. Проведем через конец вектора плоскости, параллельные координатным. Точки пересечения этих плоскостей с осями обозначим соответствен-но через М₁, М₂, М₃. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор . Тогда , , По определению суммы нескольких векторов находим Так как , то

Обозначим проекции вектора на оси соответственно a₁, a₂, a₃, тогда

. (9)

Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа а₁, а₂, а₃ называются координатами вектора , то есть координаты вектора есть его проекции на координатные оси.

Векторное равенство (9) часто записывают в координат-ном виде

Модуль вектора. Направляющие косинусы

Пусть углы вектора с осями Ox, Оу, Оz соответственно равны a, b, g. По свойству проекции вектора на ось имеем:

, ,

или, что то же самое:

, , . (10)

Числа , , называются направляющими ко-синусами вектора ().

Действия над векторами, заданными проекциями, выполняются аналогично действиям над матрицей-строкой (матрицей-столбцом).

Координаты вектора. Найдем координаты вектора , если известны координаты точек и . Имеем:

.

Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала.

Длина вектора. Далее будет доказано, что если известны ко-ординаты точек и , то длина вектора находится по формуле:

.

Пример 4.1. Начало вектора находится в точке , конец – в точке . Найти координаты вектора , его длину и направление.

Решение. Для того чтобы найти координаты вектора , нужно от координат конца вычесть координаты начала вектора:

.

Найдем длину вектора: . Теперь по формулам (10)

имеем: , , .