Тема 4. Элементы векторной алгебры Векторы
Величина, которая полностью определяется своим число-вым значением, называется скалярной, или скаляром (термин ввел У. Гамильтон в 1843 г.). Примерами скалярных величин являются площадь, длина, объем, температура, работа, масса.
Другие величины, например, сила, скорость, ускорение, опре-деляются не только своим числовым значением, но и направлени-ем. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.
Вектор
– это направленный отрезок. Если А
– начало вектора, а В
– его конец, то вектор обозначается
символом
или
.
Вектор
называется противоположным
вектору
.
Вектор, противо-положный вектору
обозначается (
).
Длиной
вектора
называется длина отрезка
и обозначается
.
Вектор, длина которого равна нулю,
называ-ется нулевым
вектором и обозначается
(или 0, когда нет сомнений в понимании
обозначения). Нулевой вектор направле-ния
не имеет. Вектор, длина которого равна
единице, называется единичным и
обозначается через
.
Единичный вектор, направле-ние которого
совпадает с направлением вектора
,
называется ортом
вектора
.
Векторы
и
называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых.
Два вектора
и
называются равными,
если они колли-неарны, одинаково
направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку O пространства, то есть векторы оп-ределены с точностью до параллельного переноса.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Линейные операции над векторами
Под линейными операциями над векторами, как обычно, понимают операции сложения и умножения вектора на число.
Геометрическая
интерпретация.
Пусть
и
– два произ-вольных вектора. Возьмем
произвольную точку O
и построим из нее вектор
.
От точки A
отложим вектор
.
Вектор
,
соединяющий начало первого вектора с
концом второго, называется суммой
векторов
и
:
(рис. 4.1).
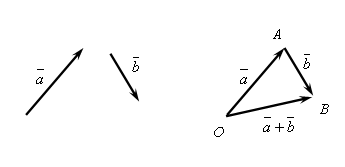
Рис. 4.1
Это правило сложения векторов называется правилом треугольника. Аналогично происходит сложение нескольких векторов (рис 4.2).
Рис. 4.2
Под
разностью векторов
и
понимается вектор
.
На практике векторы
и
откладывают из одной точки, концы
сое-диняют, и вектор имеет направление
«к концу вектора
».
Отметим,
что в параллелограмме (рис. 4.3), построенном
на векторах
и
,
одна направленная диагональ является
суммой векторов
и
,
а другая – разностью.
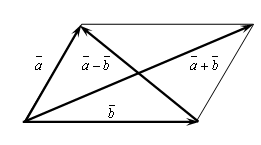
Рис. 4.3
Произведением
вектора
на скаляр (число) λ,
,
называется вектор
,
который имеет длину вектора
,
умноженную на λ,
а направление совпадает с направлением
вектора
,
если
,
и противоположно направлению вектора
,
если
.
Линейные операции над векторами обладают следующими свойствами:
|
1)
|
3)
|
|
2)
|
4)
|
|
5)
|
|
;
;
;
;
,
,
которые вполне аналогичны свойствам элементов линейного пространства.
Эти свойства позволяют проводить преобразования над векторами так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.