
- •С.А. Иванова, в.А. Павский Математика
- •Часть 1
- •Оглавление
- •Тема 10. Исследование функции 145
- •Введение
- •Тема 1. Элементы линейной алгебры Матрицы и действия над ними
- •Действия над матрицами
- •1. Сложение матриц
- •2. Умножение матрицы на число
- •3. Умножение матриц
- •Определитель матрицы
- •Свойства определителей
- •Вычисление определителей
- •Обратная матрица
- •Ранг матрицы
- •Элементарные преобразования матрицы
- •Тема 2. Системы линейных алгебраических уравнений
- •Методы решения системы линейных алгебраических уравнений
- •1. Метод Крамера
- •2. Матричный метод
- •3. Метод Гаусса
- •Однородная система линейных алгебраических уравнений
- •Системы линейных неравенств
- •Тема 3. Линейные пространства
- •Базис линейного пространства
- •Собственные значения и собственные векторы матрицы
- •Тема 4. Элементы векторной алгебры Векторы
- •Линейные операции над векторами
- •Проекция вектора на ось
- •Разложение вектора по ортам координатных осей
- •Модуль вектора. Направляющие косинусы
- •Базис системы векторов
- •Скалярное произведение векторов
- •Cвойства скалярного произведения
- •С помощью скалярного произведения находят
- •Векторное и смешанное произведение векторов
- •Свойства векторного произведения
- •Свойства смешанного произведения
- •Тема 5. Аналитическая геометрия на плоскости Система координат на плоскости
- •Уравнение линии на плоскости
- •Уравнение прямой на плоскости
- •Тема 6. Кривые второго порядка
- •Окружность
- •Гипербола
- •Парабола
- •Тема 7. Аналитическая геометрия в пространстве Уравнение поверхности и линии в пространстве
- •Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей
- •Уравнение прямой в пространстве
- •Уравнения прямой, проходящей через две данные точки
- •Деление отрезка в данном отношении
- •Тема 8. Функции. Теория пределов Понятие функции
- •Способы задания функции
- •Графический
- •Элементарные функции
- •Задание функций в полярной системе координат
- •Числовые последовательности
- •Предел числовой последовательности
- •Свойства бесконечно малых
- •Свойства сходящихся последовательностей
- •О сжатой последовательности
- •Предел функции
- •Основные теоремы о пределах
- •Вычисление пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Эквивалентные функции
- •Непрерывность функции
- •Классификация точек разрыва
- •Тема 9. Дифференциальное исчисление Определение производной
- •Геометрический смысл производной
- •Правила дифференцирования, таблица производных
- •Правила дифференцирования
- •Производные сложной и обратной функций
- •Дифференцирование неявных и параметрически заданных функций
- •Логарифмическое дифференцирование
- •Геометрические приложения производной
- •Дифференциал функции
- •Основные свойства дифференциала
- •Производные высших порядков
- •Теоремы о дифференцируемости функции
- •Правило Лопиталя
- •Формула Тейлора
- •Тема 10. Исследование функции Возрастание и убывание функции
- •Экстремумы функции
- •Наибольшее и наименьшее значения функции
- •Вогнутость и выпуклость функции. Точки перегиба
- •Асимптоты графика функции
- •Заключение
- •Задания для самостоятельной работы
- •Список литературы
- •Математика
- •Часть 1 Нач. Редакции а.С. Обвинцева
- •650010, Г. Кемерово, ул. Красноармейская, 52
Тема 3. Линейные пространства
Определение.
Непустое множество L
называется линейным (векторным)
пространством над полем действительных
чисел R,
если оно замкнуто относительно операций
сложения и умножения на чис-ло, то есть
для любых элементов
![]() и
и
![]() выполняется:
выполняется:
-
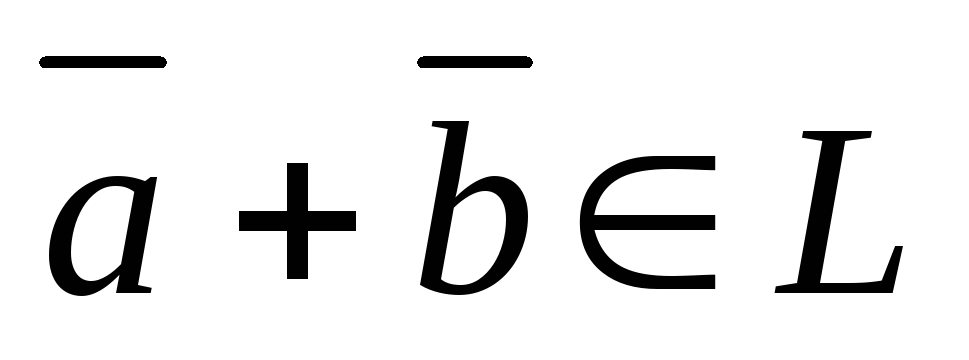 ,
причем
,
причем
-
сложение коммутативно,
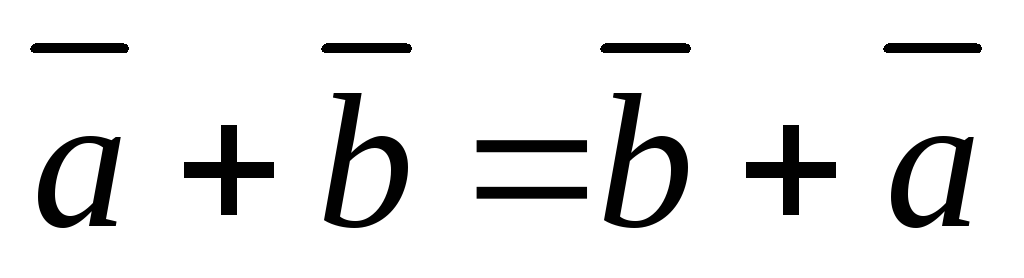 ;
; -
сложение ассоциативно,
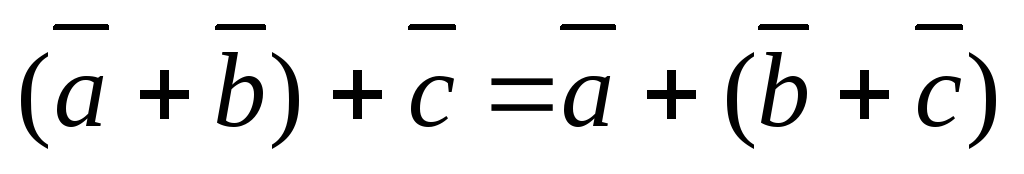 ;
; -
существует нулевой элемент
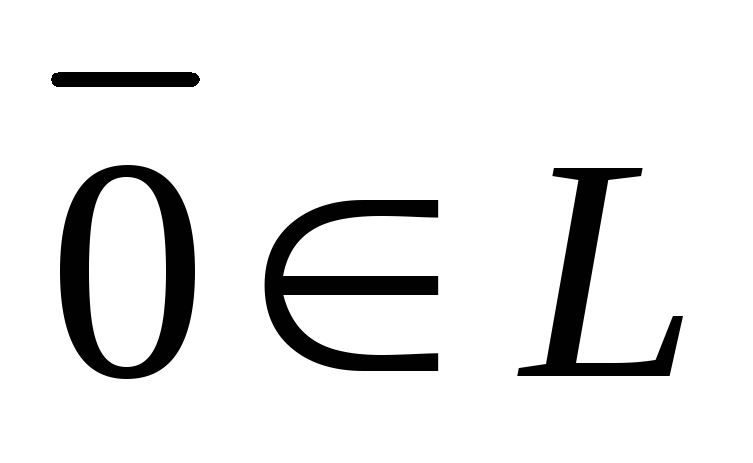 такой, что
такой, что
![]() ;
;
-
для любого
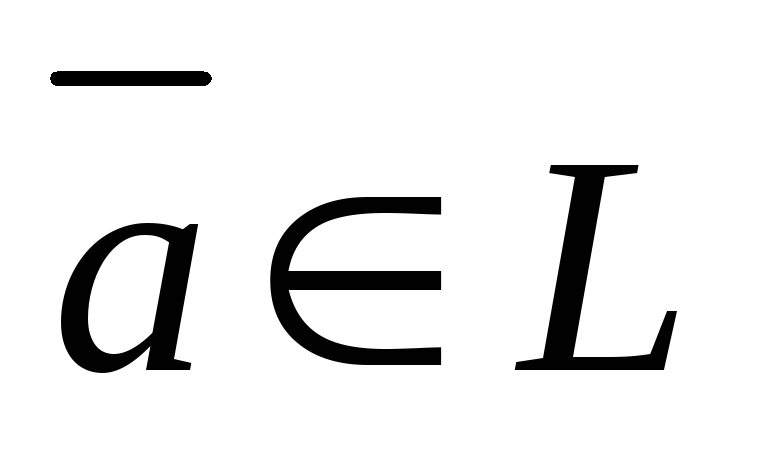 существует такой противоположный
элемент
существует такой противоположный
элемент
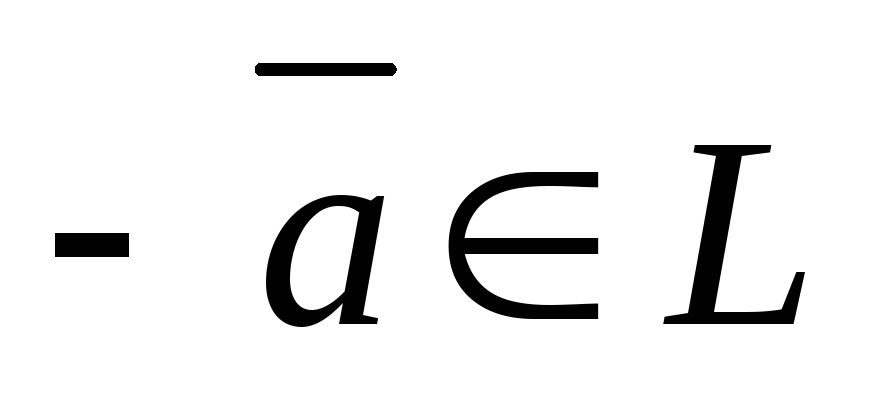 ,
что
,
что
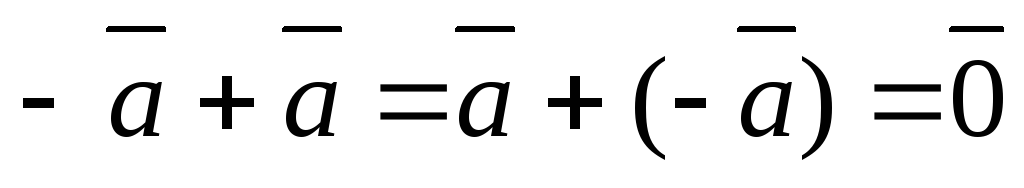 .
.
-
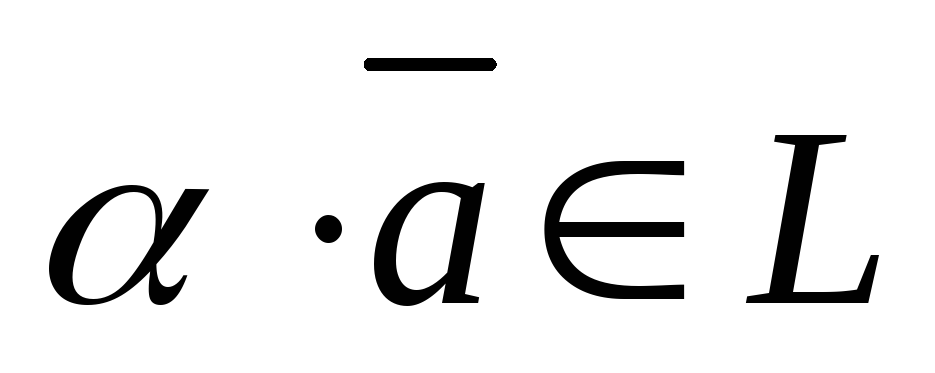 ,
причем
,
причем
-
умножение на число ассоциативно,
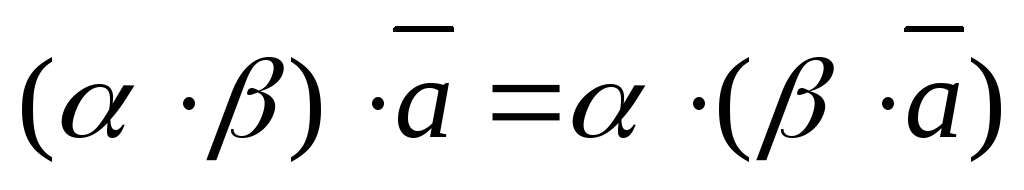 ;
; -
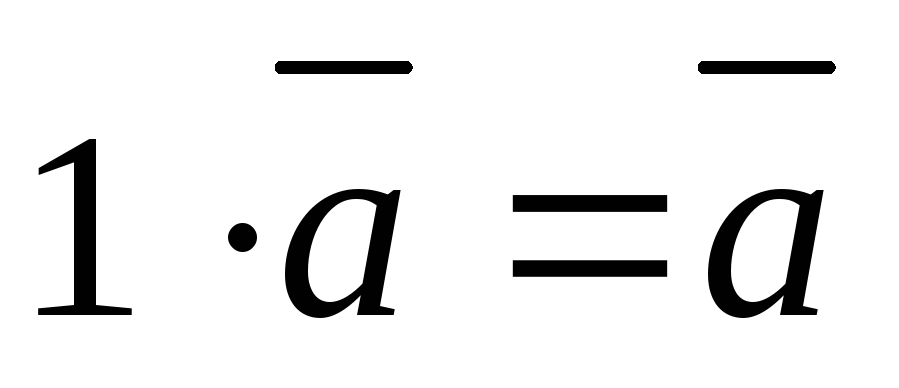 .
.
-
Связь между I и II, причем
-
умножение на число дистрибутивно относительно сложения векторов,
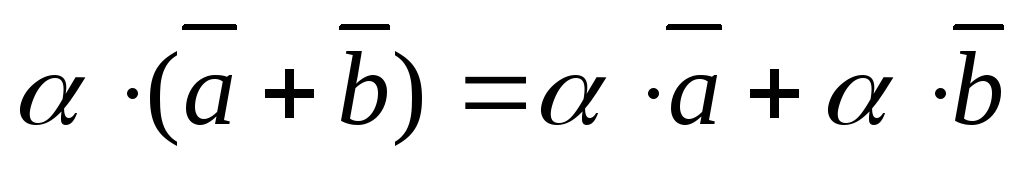 ;
; -
умножение на векторы дистрибутивно относитель-но чисел,
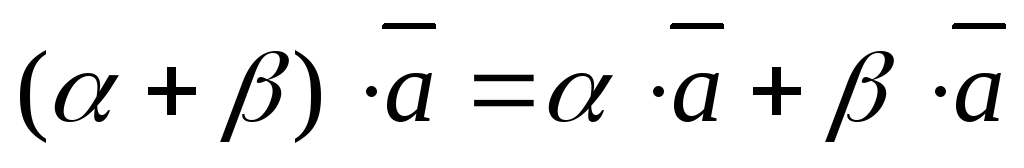 .
.
Элементы линейного пространства называются точками или векторами. Операции над элементами: сложение (I) и умно-жение на число (II) – называются линейными.
Пример 3.1
-
Рассмотрим множество матриц. Будем считать строки матрицы векторами, соответственно матрицу-строку будем назы-вать вектор-строкой, а матрицу-столбец – вектор-столбцом. Пусть L – множество матриц одной размерности, А, В Î L, l Î R, тогда
I.
![]() .
.
II.
![]() .
.
Для введенных линейных операций выполняются все дополни-тельные требования при условии, что нулевым элементом является нулевая матрица. Таким образом, множество квадратных матриц образует линейное пространство над полем действительных чисел.
-
Векторы на плоскости как направленные отрезки с операци-ями сложения и умножения на действительное число образуют дву-мерное линейное пространство над множеством действительных чисел.
Базис линейного пространства
Определение.
Выражение
вида
![]() ,
где
,
где
![]() и
и
![]() ,
,
![]() ,
называется линейной комбина-цией
векторов
,
называется линейной комбина-цией
векторов
![]() ,
,
![]() ,
…,
,
…,
![]() над полем действительных чисел.
над полем действительных чисел.
Определение.
Совокупность
(система) векторов
![]() называется линейно зависимой, если
существуют такие числа
называется линейно зависимой, если
существуют такие числа
![]() ,
одновременно не равные нулю, для которых
выполняется соотношение
,
одновременно не равные нулю, для которых
выполняется соотношение
![]() .
.
Если это равенство
выполняется только в том случае, ког-да
все коэффициенты
![]() ,
то система векторов называется линейно
независимой.
,
то система векторов называется линейно
независимой.
Определение. Линейное пространство называется n-мерным (размерности n), если в нем существует n линейно независимых элементов, а любые его (n+1) элементов – линейно зависимы.
Определение.
Базисом
системы векторов
![]() – n-мерного
линейного пространства называется
такая ее часть
– n-мерного
линейного пространства называется
такая ее часть
![]() ,
,
![]() ,
…,
,
…,
![]() ,
которая удовлетворяет следующим
условиям:
,
которая удовлетворяет следующим
условиям:
-
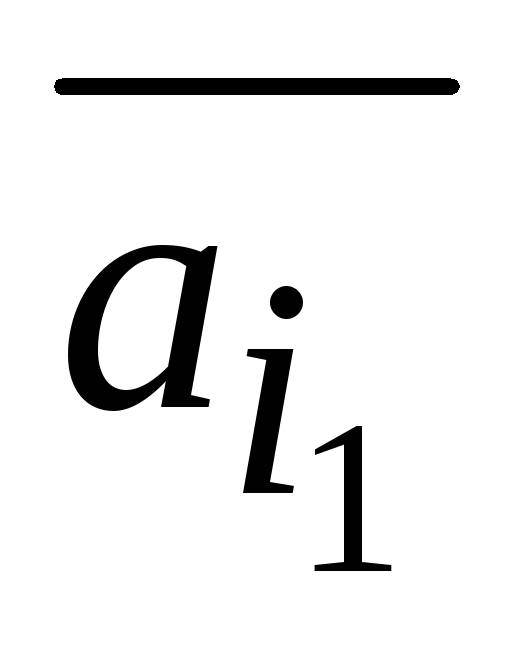 ,
,
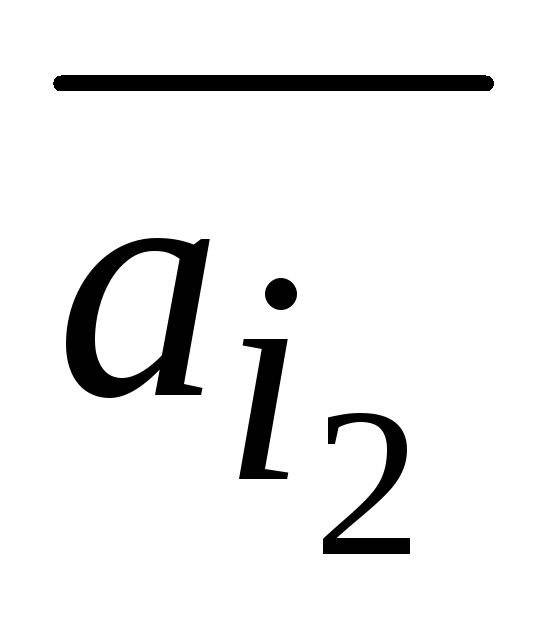 ,
…,
,
…,
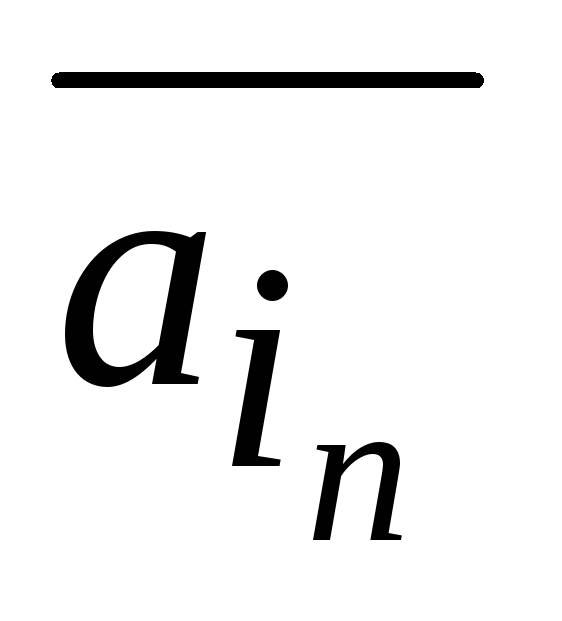 –
линейно независимая система векторов;
–
линейно независимая система векторов; -
любой вектор системы
 является линейной комбинацией линейно
независимых векторов
является линейной комбинацией линейно
независимых векторов
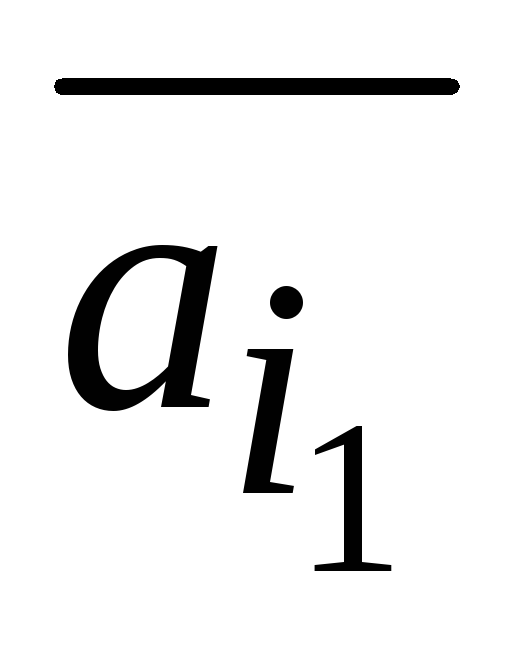 ,
,
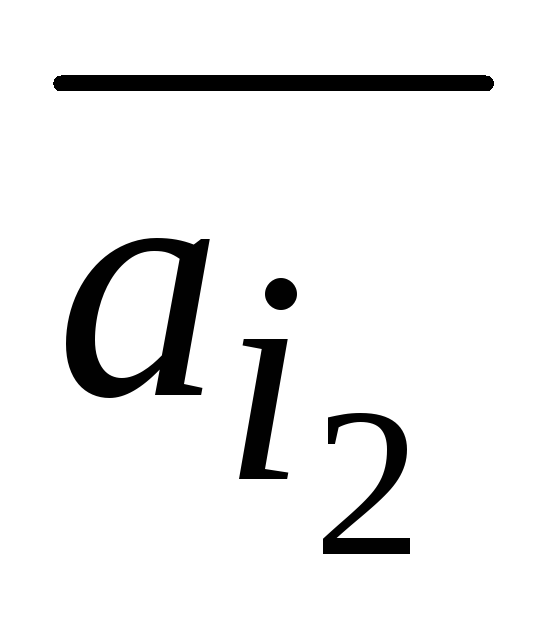 ,
…,
,
…,
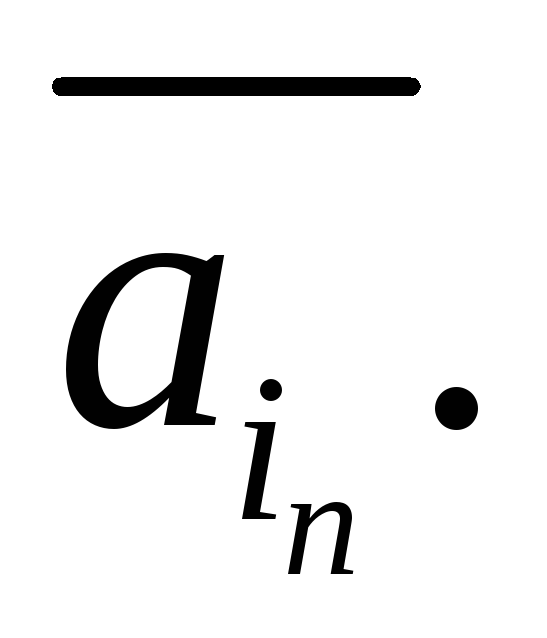
Теорема
3.1.
Каждый вектор системы
![]() единственным
образом раскладывается по векторам ее
базиса.
единственным
образом раскладывается по векторам ее
базиса.
Собственные значения и собственные векторы матрицы
Определение.
Пусть задано линейное пространство L.
Преобразованием A
этого пространства называется закон,
по которому каждому вектору
![]() соответствует вектор
соответствует вектор
![]() ,
то есть
,
то есть
![]() .
.
Преобразование A
называется линейным, если для любых
элементов
![]() и любого числа l
справедливы равенства:
и любого числа l
справедливы равенства:
-
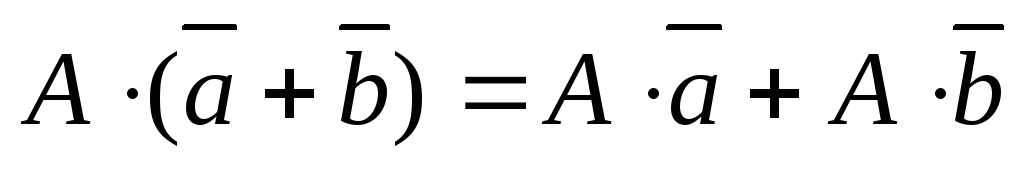 ;
; -
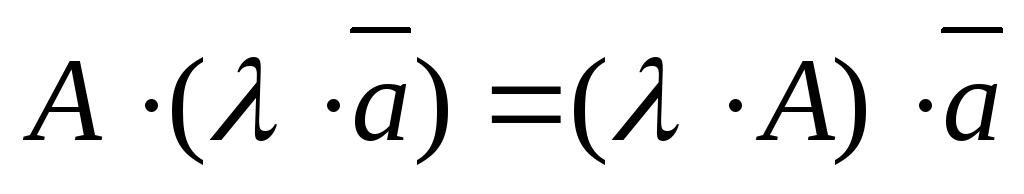 .
.
Если
L
– 3-мерное пространство (L3),
в котором выбран некоторый базис, то
связь между координатами вектора
![]() (прообраза) и координатами вектора
(прообраза) и координатами вектора
![]() (образа) определяется системой:
(образа) определяется системой:
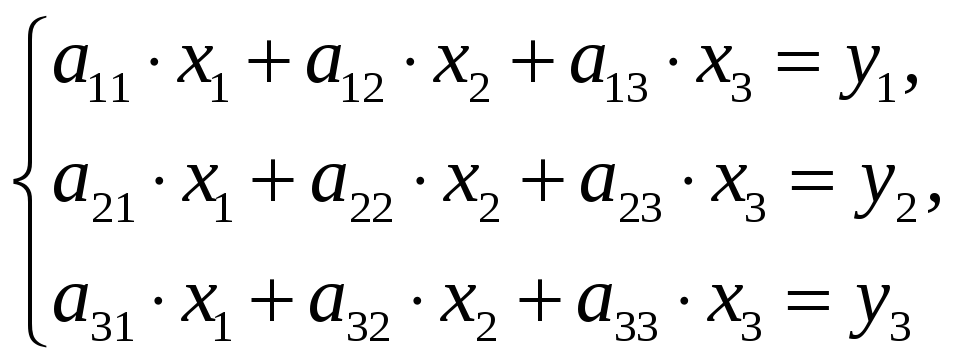
или в матричной форме:
![]()
где
 ,
,
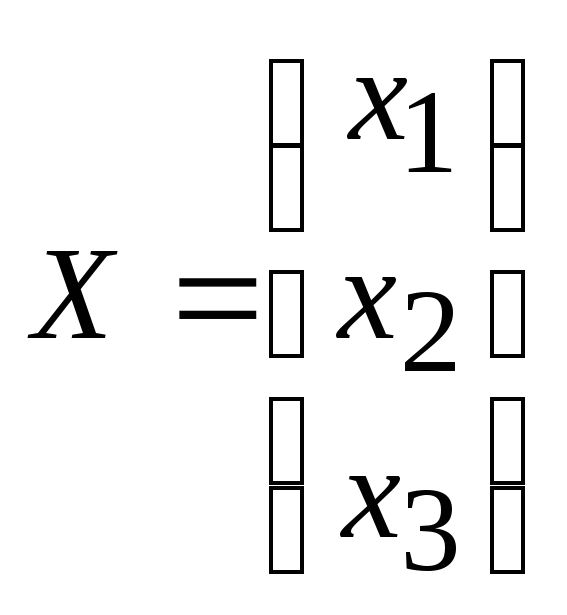 ,
,
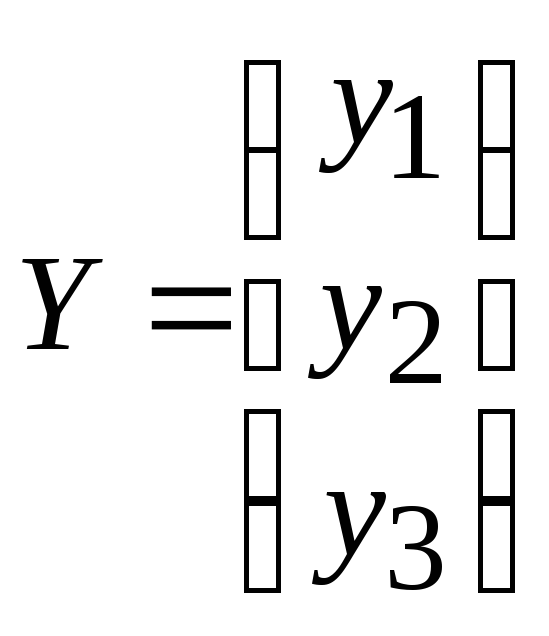 .
.
Матрица A называется матрицей линейного преобразования.
Определение.
Всякий ненулевой вектор
![]() называется соб-ственным
вектором линейного преобразования
A,
если найдется число l
такое, что выполняется равенство
называется соб-ственным
вектором линейного преобразования
A,
если найдется число l
такое, что выполняется равенство
![]() .
(6)
.
(6)
Число l
называется собственным
значением линейного преобразования
A,
соответствующим собственному вектору
![]() ,
,
![]() .
.
Если в пространстве L3 задан некоторый базис, то равенство (6) может быть записано в матричной форме:
![]() (7)
(7)
Всякий ненулевой столбец, для которого выполняется равенство (7), называется собственным вектором матрицы A, соответствующим собственному значению l.
Так как
![]() ,
где E
– единичная матрица, то уравнение (7)
можно записать в виде:
,
где E
– единичная матрица, то уравнение (7)
можно записать в виде:
![]() .
.
Перейдя к координатной форме записи, будем иметь:

где
![]() – координаты собственного вектора X,
– координаты собственного вектора X,
![]() .
.
Для отыскания собственных векторов необходимо найти ненулевые решения системы, которые существуют тогда и толь-ко тогда, когда определитель системы равен нулю, то есть
![]() (8)
(8)
или
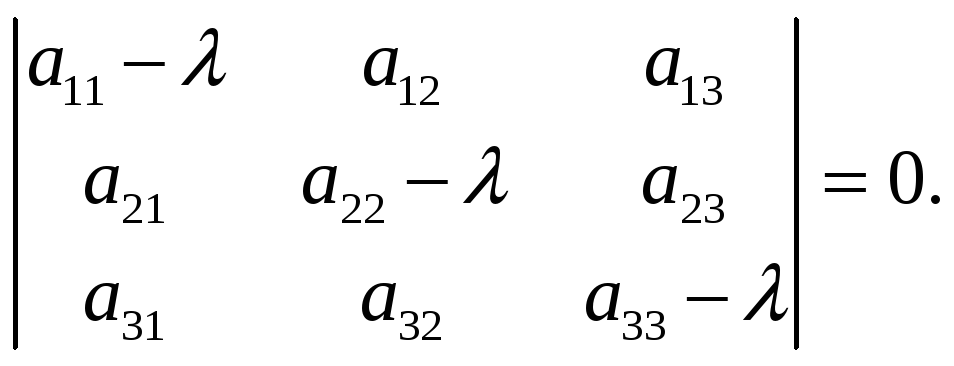
Уравнение
(8) называется характеристическим
уравнением
матрицы А,
его корни
![]() ,
,
![]() ,
,
![]() –
характеристическими
числами
или собственными
значениями
матрицы А.
–
характеристическими
числами
или собственными
значениями
матрицы А.
Пример 3.2.
Найти собственные значения и собственные
векторы матрицы
![]() .
.
Решение.
Найдем
собственные значения матрицы A,
для этого составим характеристическое
уравнение
![]() После
вычисления определителя
и приведения подобных получаем квадратное
уравнение
После
вычисления определителя
и приведения подобных получаем квадратное
уравнение
![]() Найдем
его корни.
Найдем
его корни.
Если
задано квадратное уравнение
![]() и его дискриминант
и его дискриминант
![]() ,
то корни уравнения опреде-ляются по
формуле
,
то корни уравнения опреде-ляются по
формуле
![]() .
В нашем случае
.
В нашем случае
![]() ,
,![]() ,
,
![]() .
.
Определим
собственные векторы, соответствующие
найденным собственным значениям. При
![]() получим систему, решение которой
определяет собственный вектор
получим систему, решение которой
определяет собственный вектор
![]()
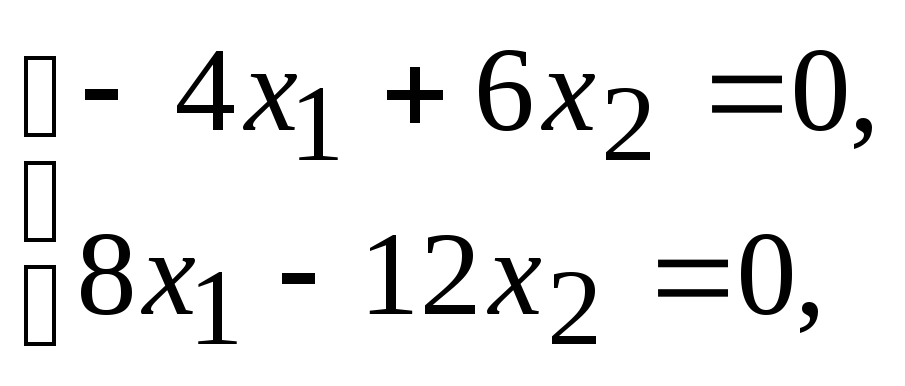 Þ
Þ
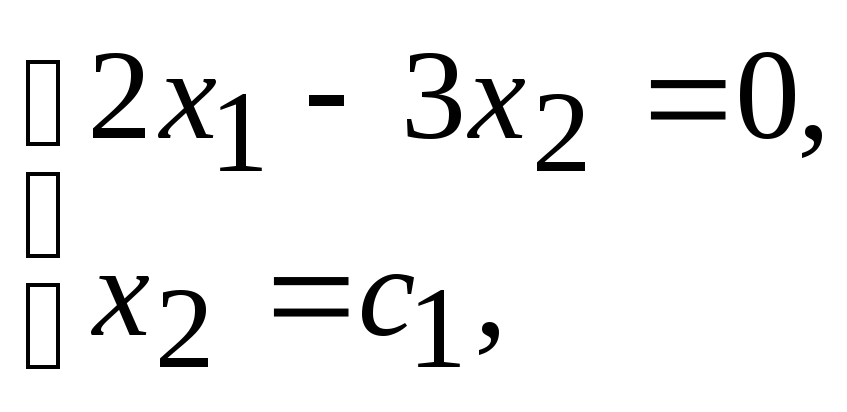 Þ
Þ
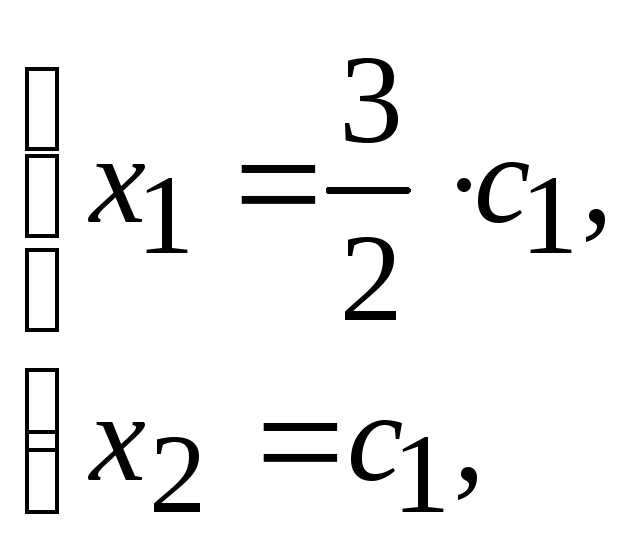
тогда
![]()
При
![]() получим систему, решение которой
определяет собственный вектор
получим систему, решение которой
определяет собственный вектор
![]() .
.
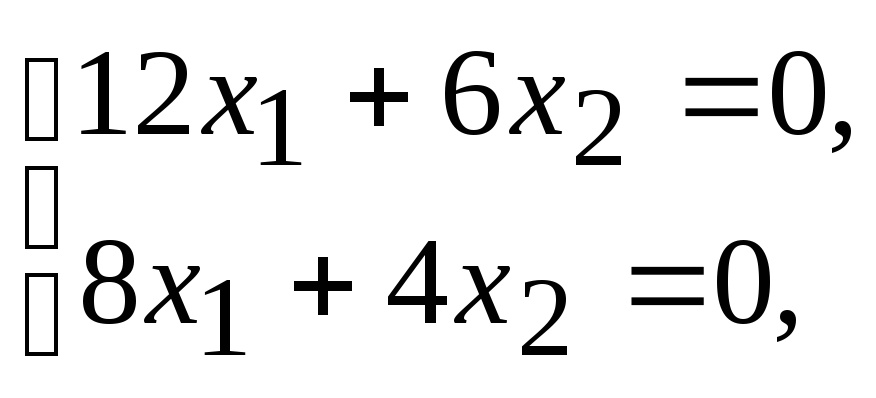 Þ
Þ
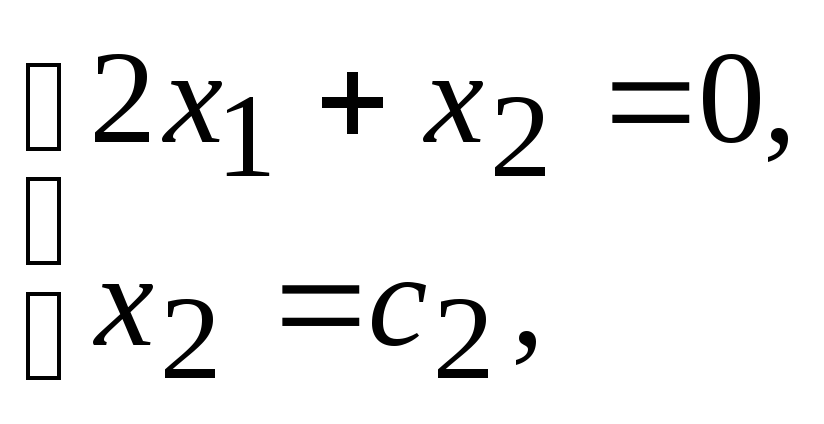 Þ
Þ
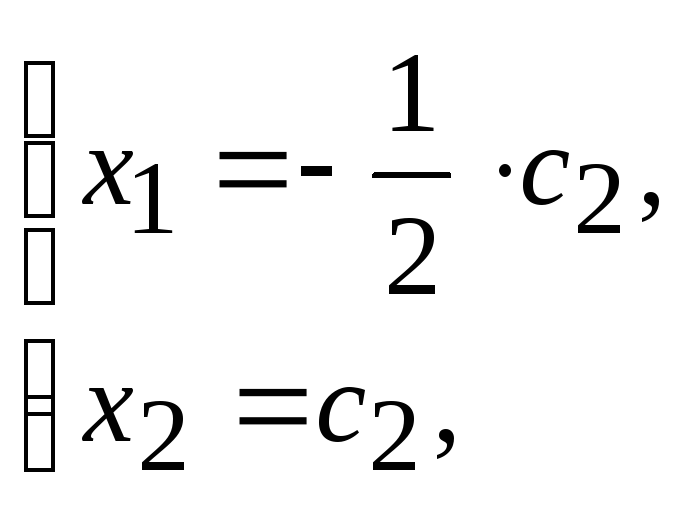
тогда
![]() .
.
Ответ:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
