Однородная система линейных алгебраических уравнений

Определение. Система линейных алгебраических уравне-ний называется однородной (ОСЛАУ), если все свободные чле-ны системы равны нулю:

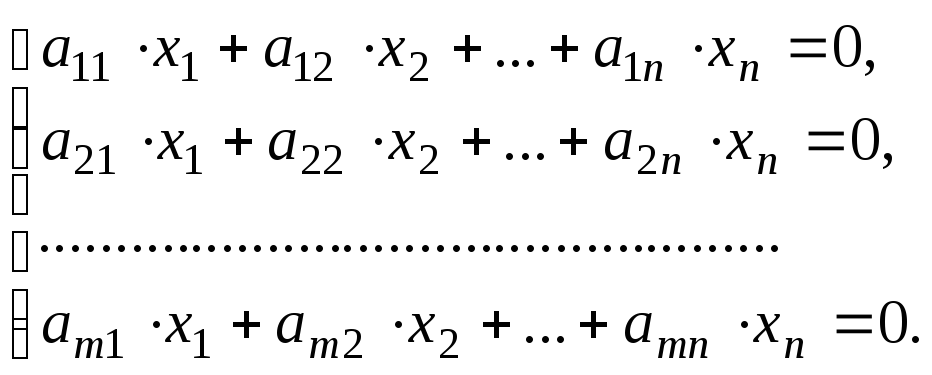(5)

Очевидно, что однородная система линейных алгебраи-ческих уравнений совместна, так как одно ее решение всегда известно: все неизвестные равны нулю.

Теорема 2.2. Однородная система (5) имеет единственное нулевое решение тогда и только тогда, когда определить матрицы коэффициентов при неизвестных не равен нулю. В противном случае у системы (5) окажется множество решений.

Пример 2.3. Решить однородную систему уравнений

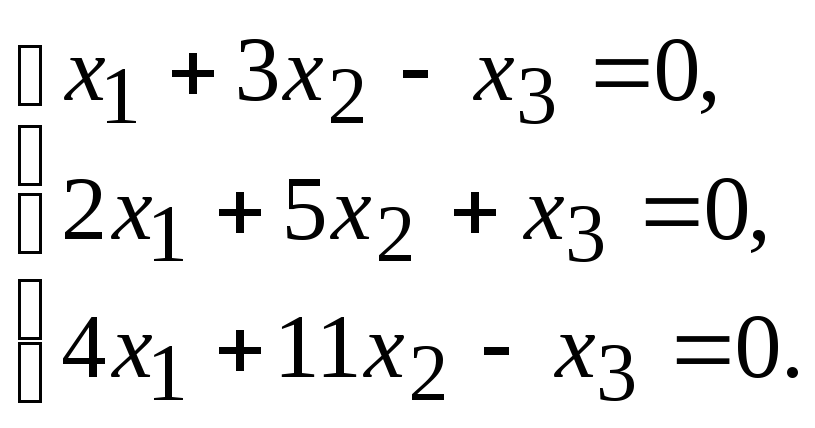
Решение. Вычислим определитель матрицы А:

.

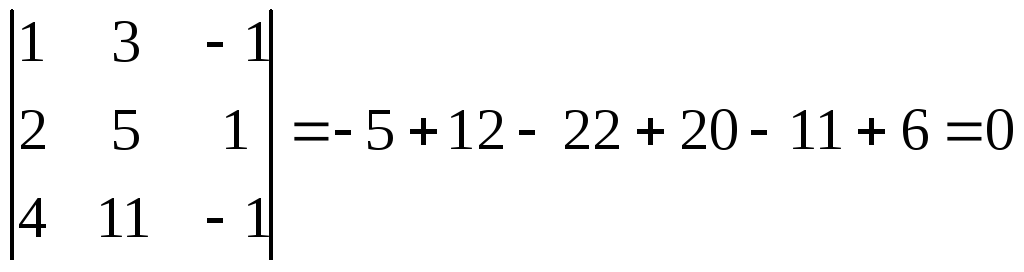Так как , то хотя бы одна из строк является линейной комбинацией других, следовательно, система имеет множество реше-ний, которые найдем, например, методом Крамера.

Решим систему из двух уравнений (оставшееся уравнение является комбинацией этих двух):

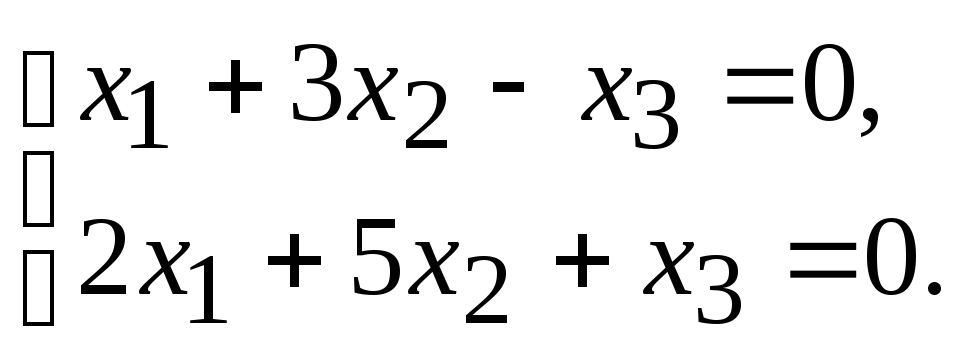
Пусть , тогда

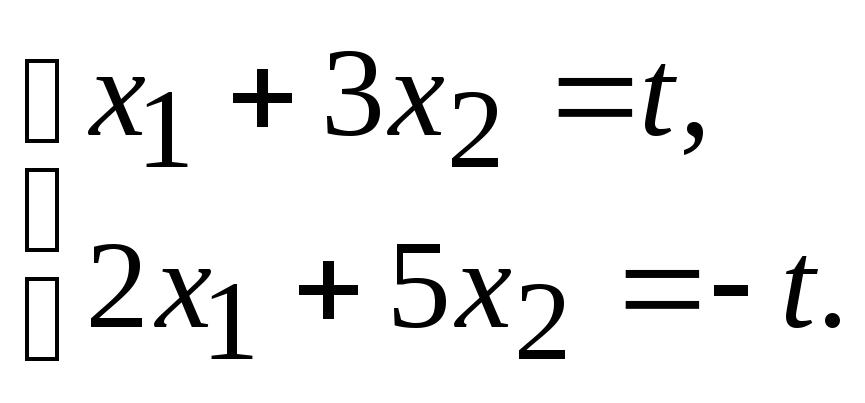
Вычислим определители

, , .

Тогда , , .

Ответ: , , .

Системы линейных неравенств

Определение. Два алгебраических выражения, соединен-ные одним из знаков <, >, £, ³, образуют неравенства. Нера-венства называются линейными, если переменные x, y входят в него в первых степенях, не перемножаясь между собой, то есть имеют вид:

, ;

, .

Решением линейного неравенства называется всякая пара значений переменных х, у, при которых оно выполнимо. Решить неравенство – значит найти множество всех его решений.

Известно, что пара действительных чисел (x, y) однознач-но определяет точку координатной плоскости, поэтому мно-жество решений линейного неравенства можно изобразить графически на координатной плоскости. В зависимости от знака неравенства графическим изображением решения линейного неравенства является одна из полуплоскостей, на которые раз-деляется плоскость соответствующей прямой.

Пусть задана система линейных неравенств:

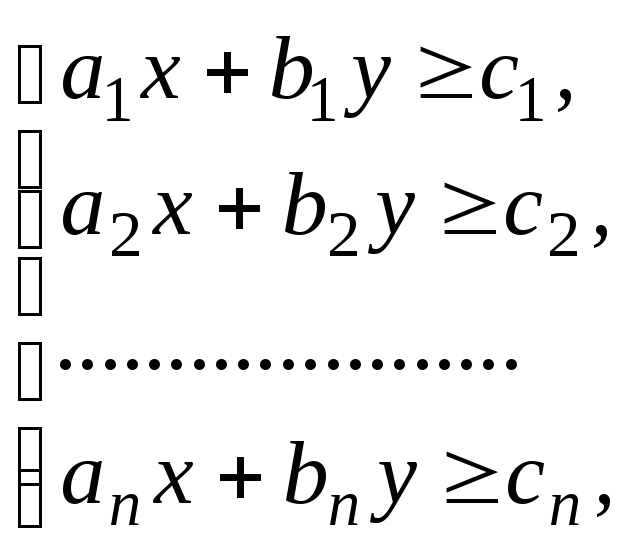
тогда решением этой системы называется упорядоченная пара чисел, удовлетворяющая каждому из неравенств этой системы, поэтому множество решений системы есть пересечение множеств решений входящих в нее неравенств. Если это пересечение пусто, то решения системы неравенств не существует.

Пример 2.4. Изобразить на координатной плоскости мно-жество решений неравенства .

Решение. Преобразуем данное неравенство к виду . Построим на координатной плоскости прямую (рис. 2.1).

Так как ордината любой точки, лежащей выше прямой , больше, чем ордината точки, имеющей такую же абсциссу, но лежащей на прямой, то множество точек плоскос-ти, расположенных выше этой прямой, и будет геометрическим изображением решений заданного неравенства.

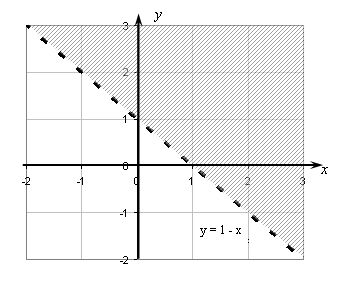
Рис. 2.1

Пример 2.5. Изобразить множество решений системы неравенств на координатной плоскости и определить координа-ты «угловых» точек этого множества:

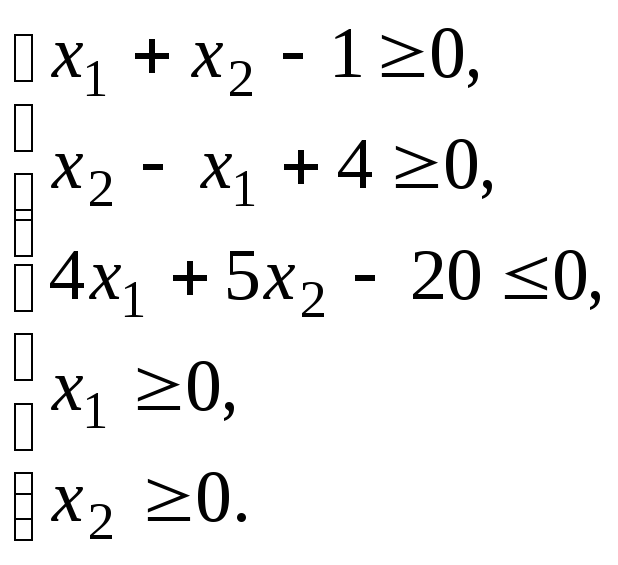
Решение. Построим на координатной плоскости прямые (1), (2), (3), (4), (5) (рис. 2.2).

Все неравенства, входящие в систему, нестрогие, поэтому сами прямые будут входить в множество решений системы. Если неравенство имеет вид , то геометрическим изображением его решения является нижняя полуплоскость, если , то – верхняя полуплоскость.

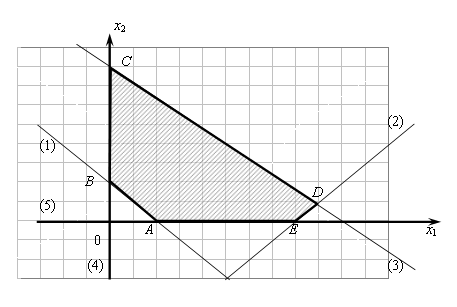
Рис. 2.2

Угловые точки полученного множества лежат на пересечении двух прямых, поэтому, чтобы найти их координаты, необходимо решить системы уравнений, их задающих.

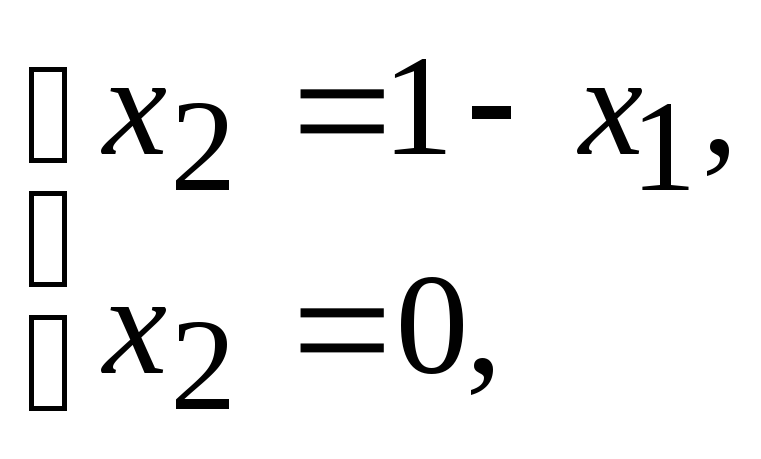
А: Þ .

B: Þ .

C: Þ .

D: Þ .

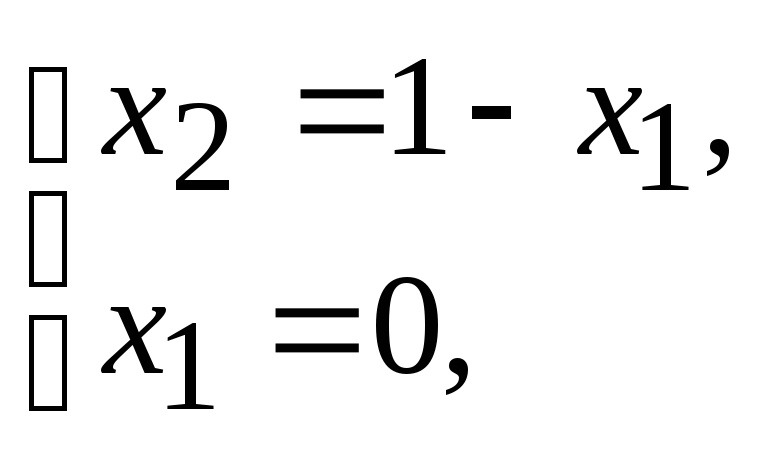
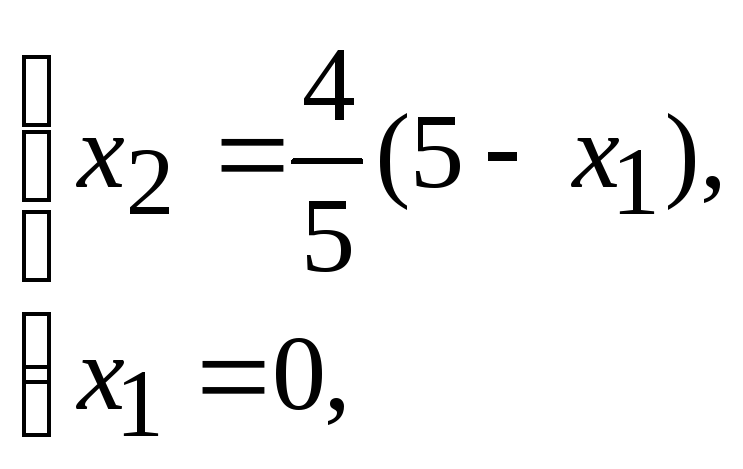
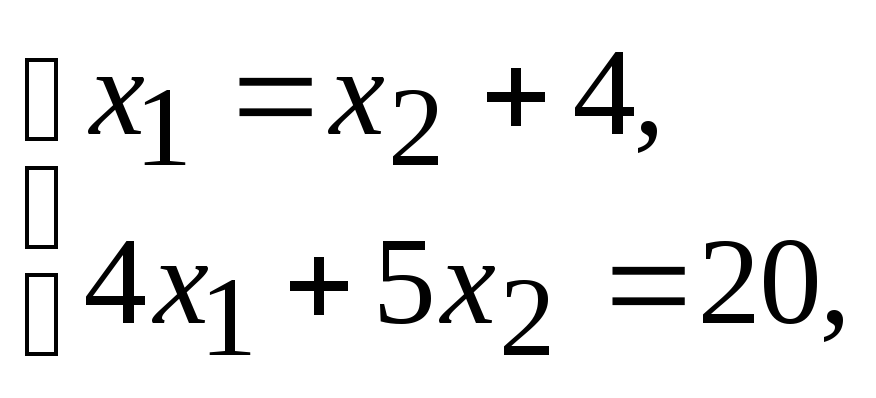
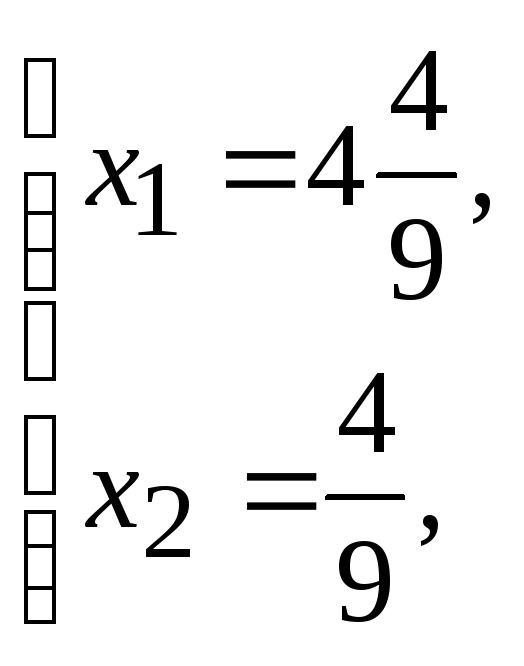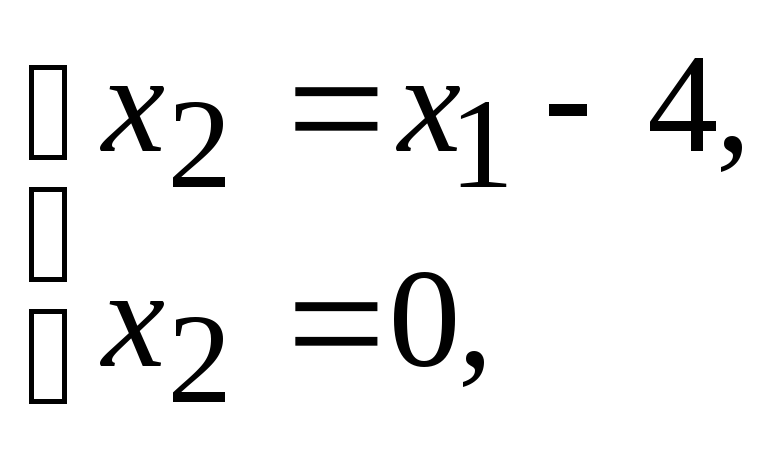
E: Þ .