Асимптоты графика функции

Определение. Асимптотой графика функции называется прямая, к которой неограниченно приближается текущая точка кривой при удалении этой функции в бесконечность.

Определение. Прямая называется вертикальной асимп-тотой графика функции , если хотя бы один из односто-ронних пределов или равен бесконечности.

Определение. Прямая, заданная уравнением , назы-вается наклонной асимптотой графика функции при , если коэффициенты k, b, определяемые по формулам , , принимают конечные значения.

Если , то – горизонтальная асимптота.

Схема исследования функции

Для того чтобы построить график функции, необходимо обладать достаточной информацией об этой функции. Такую информацию можно получить, проведя полное исследование функции, пользуясь следующей схемой:

1. область определения функции;

2. нули функции, интервалы знакопостоянства функции;

3. четность, нечетность, периодичность;

4. экстремумы, интервалы возрастания / убывания функции;

5. точки перегиба, интервалы выпуклости / вогнутости;

6. асимптоты.

Пример 10.2. Провести полное исследование функции и построить ее график.

Решение. Исследуем функцию в соответствии со схемой.

1. Функция 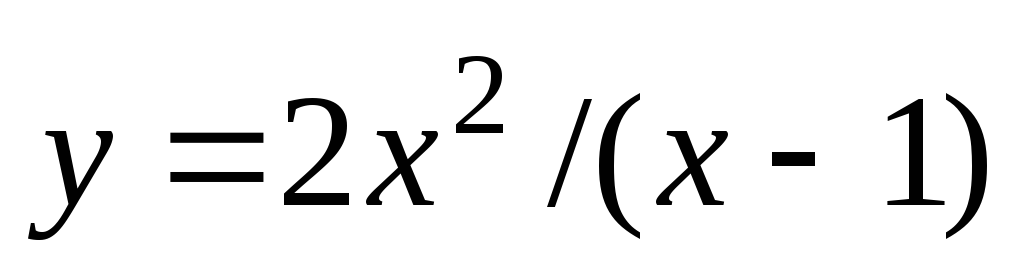не определена только в точке 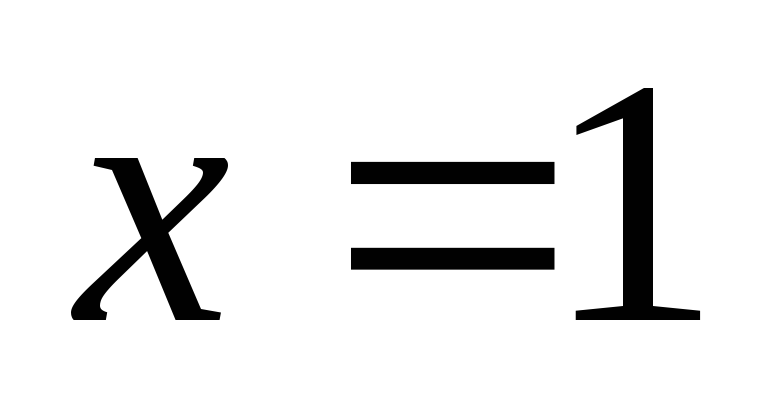, поэтому областью определения функции будет вся числовая плоскость, кроме этой точки, то есть .

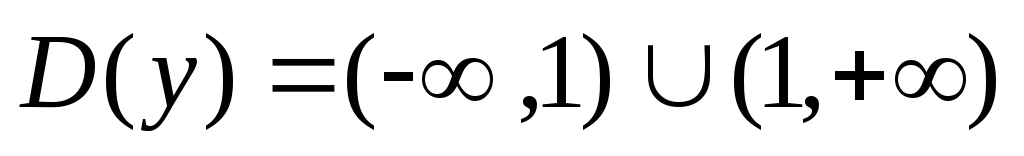2. Найдем точки пересечения графика функции с осями координат:

с осью Ох: Þ ; с осью Оу: Þ . Определим интервалы знакопостоянства функции (рис. 10.6).

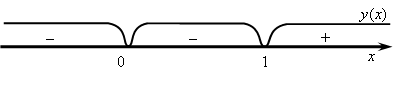
Рис. 10.6

Таким образом, график функции расположен выше оси Ox на интервале и ниже – на интервале .

3. Очевидно, что ни одна позиция не выполнена, то есть функция не является ни четной, ни нечетной, ни периодической.

4. Исследуем функцию на наличие экстремумов. Для этого вычислим первую производную:

.

Найдем точки, в которых производная равна нулю или не существует, отметим на числовой оси полученные точки и определим знак производной на каждом из полученных интервалов (рис. 10.7).

Рис. 10.7

Функция возрастает на интервалах , убывает , в точке , достигает мак-симум, в точке , достигает минимум.

5. 

.

Найдем точки, в которых вторая производная функции равна нулю или не существует, полученную точку отметим на числовой оси и проверим знак второй производной на полученных интервалах (рис. 10.8).

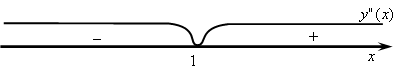
Рис. 10.8

График функции – выпуклый на интервале , вогнутый – на интервале ; так как функция в точке не определена, то точек перегиба нет.

6. Поскольку функция не определена в точке 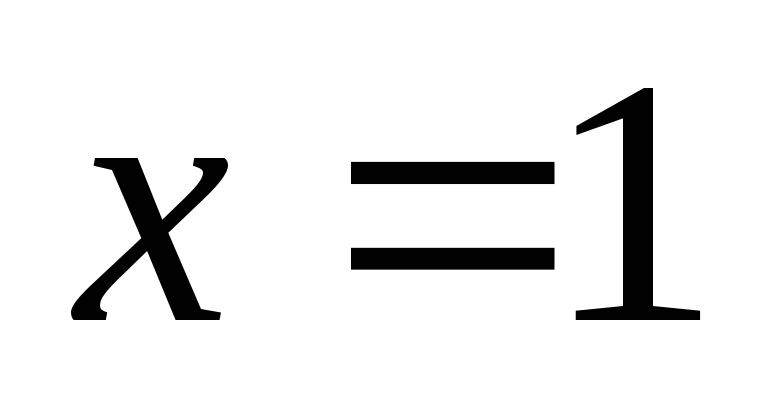, вычислим пределы функции справа и слева в этой точке.

, .

Прямая является вертикальной асимптотой.

Исследуем функцию на наличие наклонной асимптоты, для этого вычислим коэффициенты k и b.

; .

Прямая является наклонной асимптотой.

Результаты исследования представим в следующей таблице:

x		0	(0, 1)	(1, 2)	2
y	– ­	0	– ¯	+ ¯	8	+ ­
	+	Max	–	–	Min	+
	–		–	+		+

Построим график функции 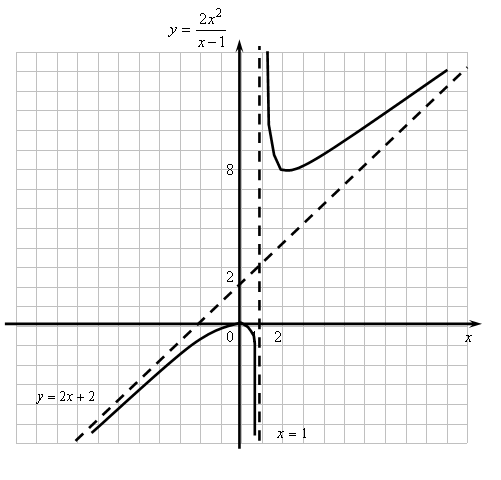(рис. 10.9).

Рис. 10.9