Теоремы о дифференцируемости функции

Знание производной дифференцируемой функции в лю-бой точке интервала часто позволяет делать выводы о по-ведении на нем самой функции. Обоснованию этого заявления и посвящена оставшаяся часть пособия.

Теорема 9.3 (Фермá). Если функция определена и непрерывна на отрезке , достигает наибольшего (наи-меньшего) значения в точке и имеет в ней конечную производную, то производная функции в этой точке равна нулю, то есть .

Теорема 9.4 (Рóлля). Если функция определена и непрерывна на отрезке , дифференцируема на интервале и на концах промежутка принимает равные значения , то существует хотя бы одна точка , производная функции в которой равна нулю, то есть .

Теорема 9.5 (Лагранжа). Если функция опреде-лена, непрерывна на отрезке , дифференцируема на интер-вале , то существует точка , в которой выпол-няется равенство

. (21)

Геометрический смысл теоремы Лагранжа состоит в том, что для дифференцируемой функции, определенной на , существует точка x, содержащаяся внутри интервала , такая, что касательная к кривой в этой точке параллельна секущей AB (рис. 9.4), что следует из равенства .

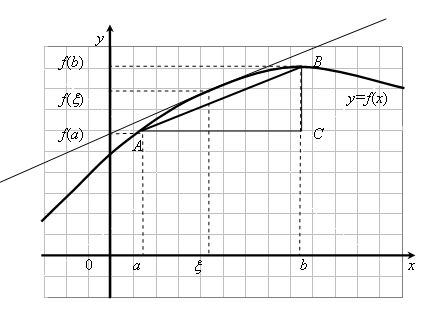
Рис. 9.4

Замечание. Теорему Лагранжа часто называют теоремой о среднем значении, а формулу (21) – формулой Лагранжа о конечных приращениях. Этому названию можно дать следующее объяснение.

Рассмотрим промежуток . Применим к нему теорему Лагранжа (при любом допустимом ), будем иметь точное равенство

,

где , или

.

Недостаток формулы Лагранжа заключается в том, что  неизвестно, так как неизвестно число . Тем не менее, формула конеч-ных приращений очень важна в теоретических исследованиях.

Теорема 9.6 (Кошú). Пусть функции , определены, непрерывны на отрезке и дифференцируемы на интервале , причем , тогда существует точка , в которой выполняется равенство

.

Геометрический смысл теоремы Коши аналогичен теореме Лагранжа.

Правило Лопиталя

Пусть функции , дифференцируемы и в некоторой окрестности точки . Если или , тогда предел отношения этих функций равен пределу отношения их производных

при условии, что существует .

Замечание. Отметим, что правило Лопиталя применяется только в том случае, если имеет место неопределенное выражение вида или .

Например, вычислить предел, используя правило Лопиталя, .

Формула Тейлора

Формула Тейлора

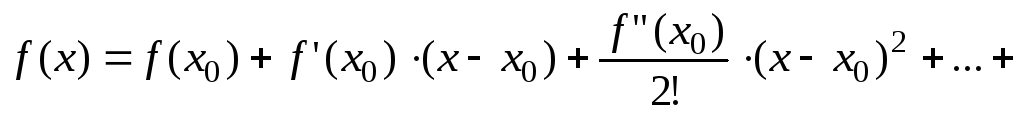
имеет большое теоретическое и практическое значение. В частности, с ее помощью можно вычислить приближенное значение функции по известным значениям этой функции и ее n производных в точке и оценивать точность этого вычисления.

Для оценки погрешности формулы Тейлора важна форма записи остаточного члена Распространенной является запись остаточного члена в форме Лагранжа:

,

где Q – произвольное число из интервала .

Пример 9.12. Применяя формулу Тейлора с остаточным членом в форме Лагранжа, вычислить e^0,1 с точностью до 0,001.

Решение. Формула Тейлора с остаточным членом в форме Лагранжа для функции при имеет вид

,

, .

Для любого значения х, находящегося в промежутке 0 < x < 1, имеем 1<e^x<3, и, следовательно, . Очевидно, условие будет выполнено, если или .

Вычисляя последовательно слагаемые, входящие в формулу Тейлора, одновременно имеем возможность видеть, достигнута ли требуемая точность d. Полагая d = 0,001 и х = 0,1, получаем, что заданная точность вычислений будет достигнута при , тогда имеем:

.