Геометрические приложения производной

Исходя из геометрического смысла производной, уравнение касательной к графику дифференцируемой функции в точке , где , имеет вид:

. (19)

В самом деле, любая прямая, заданная уравнением , однозначно определена точкой , лежащей на этой прямой, и углом ее наклона к оси Ox. Из геометрического смысла производной в точке имеем . Приравнивая левую и правую части последнего равенства, получаем (19).

Прямая, проходящая через точку перпендикулярно к каса-тельной, называется нормалью к графику функции в этой точке.

Если , то уравнение нормали имеет вид:

, (20)

если , то нормалью является прямая .

Пример 9.9. Найти уравнение касательной и нормали к графику функции в точке . Сделать чертеж.

Решение. Для того чтобы записать уравнения касательной и нормали, необходимо определить значения функции и ее производной в заданной точке : , , . Так как , то найденные значения подставим в фор-мулы (19) и (20):

– касательная,

– нормаль.

Выполним чертеж (рис. 9.3).

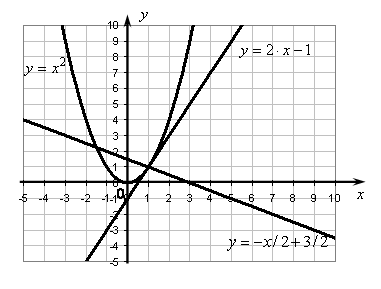
Рис. 9.3

Дифференциал функции

Определение. Функция , определенная на интервале , называется дифференцируемой в точке , если в некоторой окрестности этой точки приращение функции можно представить в виде

,

где – постоянная, при .

Определение. Дифференциалом функции в точ-ке называется главная линейная часть ее приращения и обозначается или , т. е. .

Пусть функция имеет в точке отличную от нуля производную . Тогда по теореме о связи функции, ее предела и бесконечно малой функции можно записать при или .

Таким образом, дифференциал функции в точке равен произведению производной этой функции в точке x на приращение аргумента

Поскольку дифференциал независимого переменного совпадает с его приращением (), тогда

.

Из этого равенства следует, что производную можно рассматривать не только как обозначение производной функции в точке x, но и как отношение дифференциала функции к дифференциалу независимой переменной, то есть .

Правила нахождения дифференциалов непосредственно вытека-ют из соответствующих правил дифференцирования функций.

Пример 9.10. Найти дифференциал функции .

Решение. Имеем:

.

Замечание. Рассматривая производную как отношение диф-ференциалов, легко получить многие формулы и теоремы вычисления производных. Например, производная сложной функции легко получается из цепочки: .

Основные свойства дифференциала

Пусть – дифференцируемые функции,

1)	;	2)
3)	;	4)
5)	, .

Производные высших порядков

Производная функции тоже есть функция от x и называется производной 1-го порядка (1-й производной).

Если функция дифференцируемая, то ее производ-ная называется производной 2-го порядка (2-й производной) и обозначается , или .

Производная от производной 2-го порядка, если она существует, называется производной 3-го порядка и обоз-начается , или .

По индукции производной n-го порядка называется про-изводная от производной (n-1) порядка:, .

Производные функции порядка выше первого называются производными высших порядков.

Например, для функции имеем: ; ; и т. д.

Пример 9.11. Найти производную 2-го порядка функции .

Решение. Поскольку , то .

Если функция задана параметрически: , , , функции , дифференцируемые, по крайней мере, n-го порядка включительно, , тогда производные , , , … вычисляются по формулам:

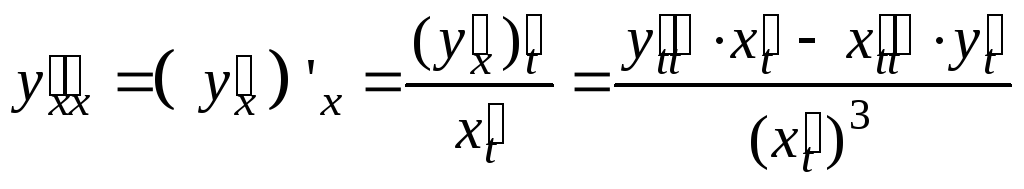, и т. д.

Например, для функции , имеем:

; .
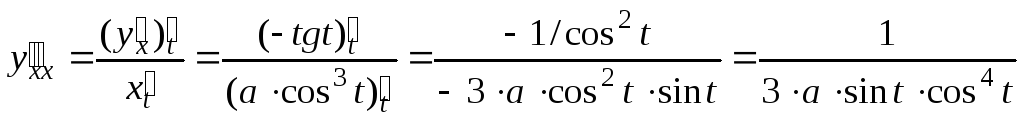