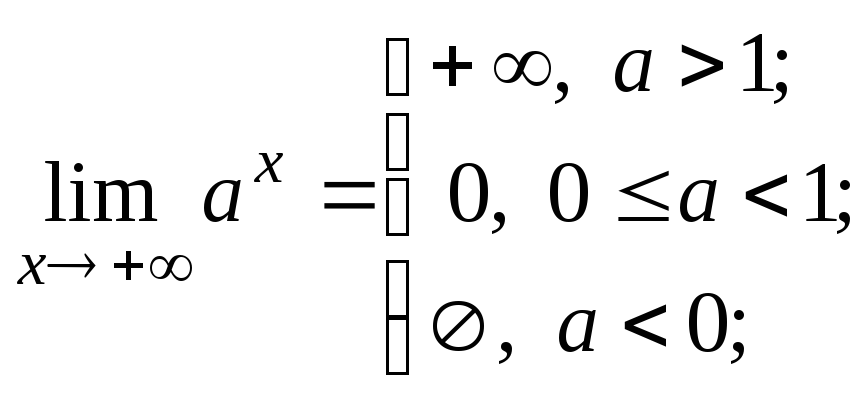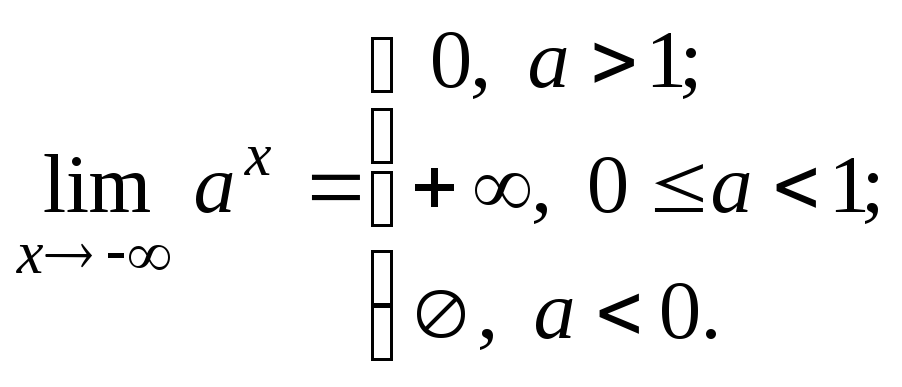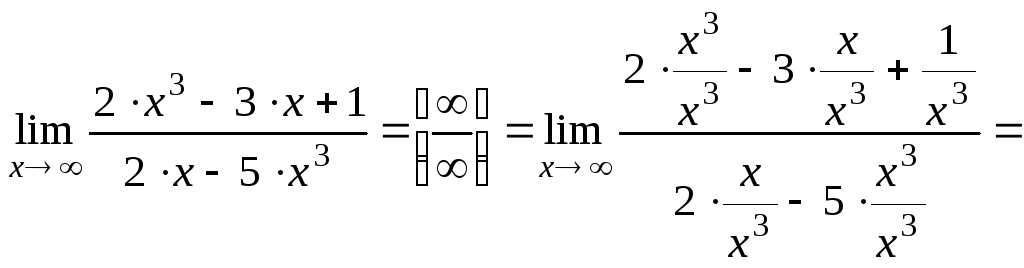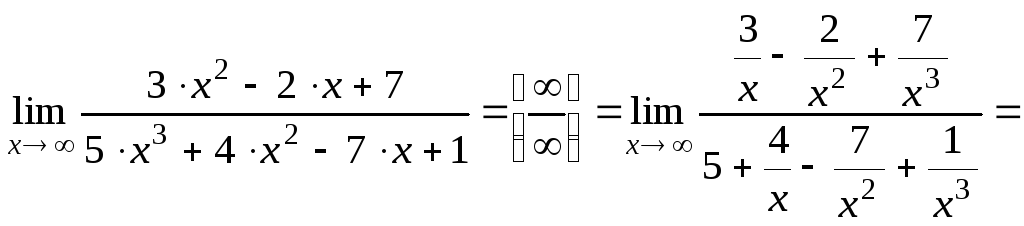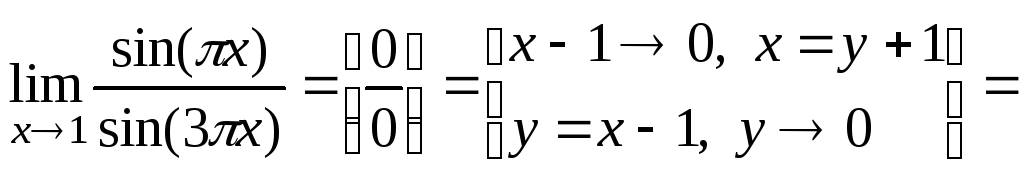- •С.А. Иванова, в.А. Павский Математика
- •Часть 1
- •Оглавление
- •Тема 10. Исследование функции 145
- •Введение
- •Тема 1. Элементы линейной алгебры Матрицы и действия над ними
- •Действия над матрицами
- •1. Сложение матриц
- •2. Умножение матрицы на число
- •3. Умножение матриц
- •Определитель матрицы
- •Свойства определителей
- •Вычисление определителей
- •Обратная матрица
- •Ранг матрицы
- •Элементарные преобразования матрицы
- •Тема 2. Системы линейных алгебраических уравнений
- •Методы решения системы линейных алгебраических уравнений
- •1. Метод Крамера
- •2. Матричный метод
- •3. Метод Гаусса
- •Однородная система линейных алгебраических уравнений
- •Системы линейных неравенств
- •Тема 3. Линейные пространства
- •Базис линейного пространства
- •Собственные значения и собственные векторы матрицы
- •Тема 4. Элементы векторной алгебры Векторы
- •Линейные операции над векторами
- •Проекция вектора на ось
- •Разложение вектора по ортам координатных осей
- •Модуль вектора. Направляющие косинусы
- •Базис системы векторов
- •Скалярное произведение векторов
- •Cвойства скалярного произведения
- •С помощью скалярного произведения находят
- •Векторное и смешанное произведение векторов
- •Свойства векторного произведения
- •Свойства смешанного произведения
- •Тема 5. Аналитическая геометрия на плоскости Система координат на плоскости
- •Уравнение линии на плоскости
- •Уравнение прямой на плоскости
- •Тема 6. Кривые второго порядка
- •Окружность
- •Гипербола
- •Парабола
- •Тема 7. Аналитическая геометрия в пространстве Уравнение поверхности и линии в пространстве
- •Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей
- •Уравнение прямой в пространстве
- •Уравнения прямой, проходящей через две данные точки
- •Деление отрезка в данном отношении
- •Тема 8. Функции. Теория пределов Понятие функции
- •Способы задания функции
- •Графический
- •Элементарные функции
- •Задание функций в полярной системе координат
- •Числовые последовательности
- •Предел числовой последовательности
- •Свойства бесконечно малых
- •Свойства сходящихся последовательностей
- •О сжатой последовательности
- •Предел функции
- •Основные теоремы о пределах
- •Вычисление пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Эквивалентные функции
- •Непрерывность функции
- •Классификация точек разрыва
- •Тема 9. Дифференциальное исчисление Определение производной
- •Геометрический смысл производной
- •Правила дифференцирования, таблица производных
- •Правила дифференцирования
- •Производные сложной и обратной функций
- •Дифференцирование неявных и параметрически заданных функций
- •Логарифмическое дифференцирование
- •Геометрические приложения производной
- •Дифференциал функции
- •Основные свойства дифференциала
- •Производные высших порядков
- •Теоремы о дифференцируемости функции
- •Правило Лопиталя
- •Формула Тейлора
- •Тема 10. Исследование функции Возрастание и убывание функции
- •Экстремумы функции
- •Наибольшее и наименьшее значения функции
- •Вогнутость и выпуклость функции. Точки перегиба
- •Асимптоты графика функции
- •Заключение
- •Задания для самостоятельной работы
- •Список литературы
- •Математика
- •Часть 1 Нач. Редакции а.С. Обвинцева
- •650010, Г. Кемерово, ул. Красноармейская, 52
Основные теоремы о пределах
Если существуют
![]() и
и
![]() ,
то справедливы следующие теоремы:
,
то справедливы следующие теоремы:
-
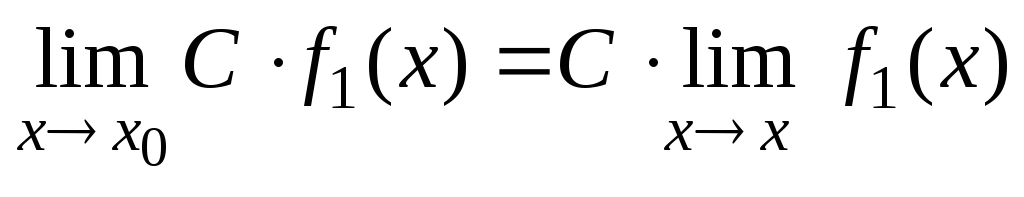 ,
,
 ;
; -
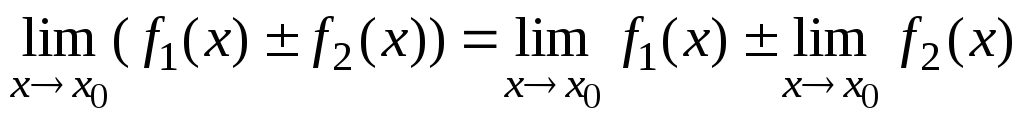 ;
; -
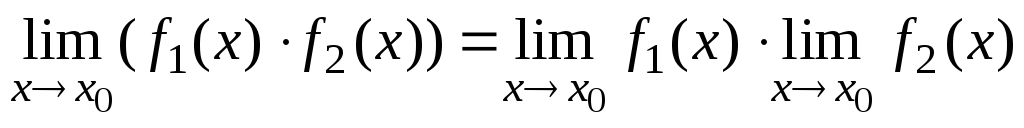 ;
; -
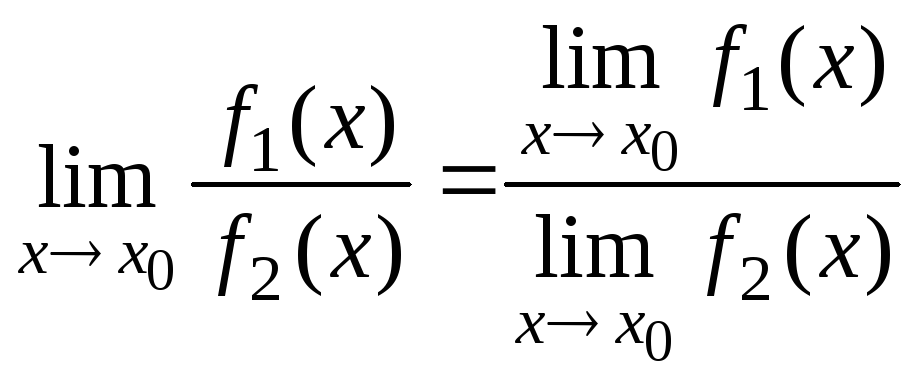 ,
(
,
( ).
).
Вычисление пределов
При вычислении пределов функции необходимо в выражение, стоящее под знаком предела, вместо переменной подставить ее предельное значение. При этом возможны два варианта:
1. Проведение необходимых вычислений позволяет полу-чить определенное число (в частности, ноль) или бесконечность, что и является ответом.
2. В результате
подстановки предельного значения
пере-менной получаются неопределенные
выражения, символические обозначения
некоторых из них имеют вид
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() и др. В этом случае для получения
результата нужно эти неопределенные
выражения «раскрыть» (то есть исключить
неоп-ределенность) либо показать, что
предела не существует.
и др. В этом случае для получения
результата нужно эти неопределенные
выражения «раскрыть» (то есть исключить
неоп-ределенность) либо показать, что
предела не существует.
Замечание.
При вычислении пределов функций полезно
помнить, что по определению (![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 8.7. Вычислить:
-
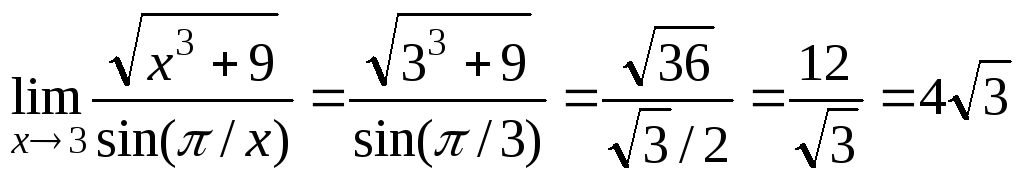 ;
;
-
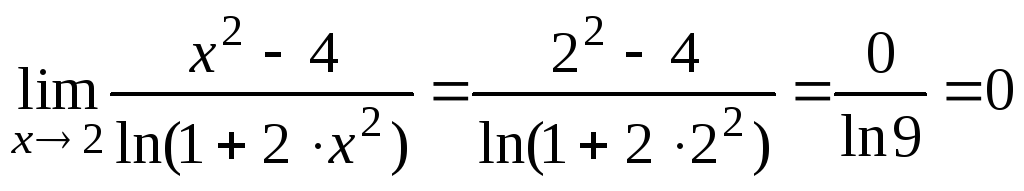 ;
;
Замечание.
Символическая запись
![]() (
(![]() ,
где
,
где
![]() – б.м. при
– б.м. при
![]() ),
стоящая под знаком предела, означает
деление не на ноль, а на число, стремящееся
к нулю, так и
),
стоящая под знаком предела, означает
деление не на ноль, а на число, стремящееся
к нулю, так и
![]() (
(![]() ,
,
![]() – б.б. при
– б.б. при
![]() )
– это не деление на бесконечность, а
деление на число, стремящееся к
бесконечности, при этом
)
– это не деление на бесконечность, а
деление на число, стремящееся к
бесконечности, при этом
![]() и
и
![]() .
.
Теперь рассмотрим методы раскрытия различных видов неопределенностей.
Неопределенность
вида
![]() .
При вычислении пределов отношения
многочленов с неопределенностью
.
При вычислении пределов отношения
многочленов с неопределенностью
![]() при
при
![]() определяют старшую степень переменной
x
для числителя и знаменателя и делят
числитель и знаменатель дроби, стоящей
под знаком предела, на x
в этой степени.
определяют старшую степень переменной
x
для числителя и знаменателя и делят
числитель и знаменатель дроби, стоящей
под знаком предела, на x
в этой степени.
Пример 8.8. Вычислить:
 ;
;
-
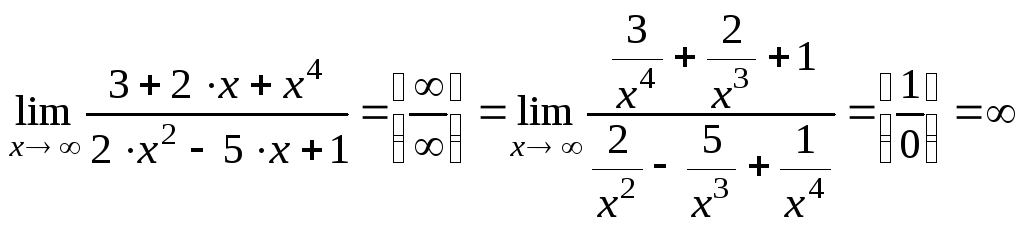 ;
;
![]() .
.
Неопределенность
вида
![]() .
При вычислении пределов отношения
многочленов с неопределенностью
.
При вычислении пределов отношения
многочленов с неопределенностью
![]() при
при
![]() необходимо при помощи алгебраических
преобразований пред-ставить эти
многочлены в виде произведения
сомножителей, одним из которых будет
(
необходимо при помощи алгебраических
преобразований пред-ставить эти
многочлены в виде произведения
сомножителей, одним из которых будет
(![]() ).
).
Пример 8.9. Вычислить:
![]() ;
;
![]() ;
;
![]()
![]()
![]() .
.
Первый замечательный предел
Теорема 8.4. Предел отношения синуса бесконечно малого угла к величине этого угла в радианах равен единице, то есть
![]() .
.
Этот предел называется первым замечательным пределом.
Легко показать (покажите), что имеют место следующие пределы:
|
|
|
|
|
|
||
Пример 8.10. Вычислить:
![]()
![]() ;
;
![]()
![]()
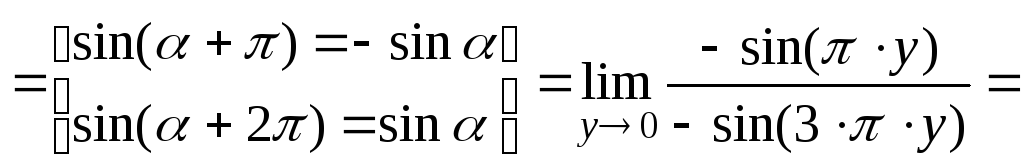
![]() .
.
Второй замечательный предел
Так называется предел
![]() ,
,
где число e
нами определено как предел последовательности
![]() (см. пример 8.6).
(см. пример 8.6).
Обычно
![]() или следствие из него
или следствие из него
![]() используется для раскрытия неопределенности
вида
используется для раскрытия неопределенности
вида
![]() .
.
Очевидно, что
структура предела предполагает, чтобы
основание степени было представлено в
виде
![]() ,
где
,
где
![]() ,
а показатель степени должен быть
величиной, обрат-ной к
,
а показатель степени должен быть
величиной, обрат-ной к
![]() .
.
Пример 8.11. Вычислить:
![]()
![]()
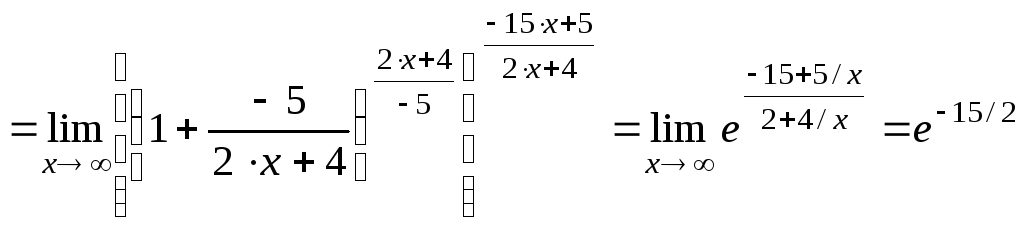 ;
;
![]()
 .
.