Элементарные функции

Определение. Функции, построенные из простейших эле-ментарных функций и постоянных при помощи конечного чис-ла арифметических действий и конечного числа операций взя-тия функции от функции, называются элементарными.

Простейшими считаются функции:

1. степенная , ;

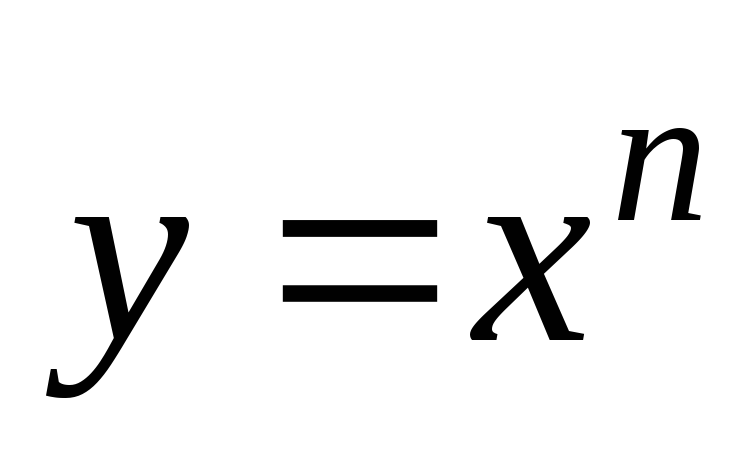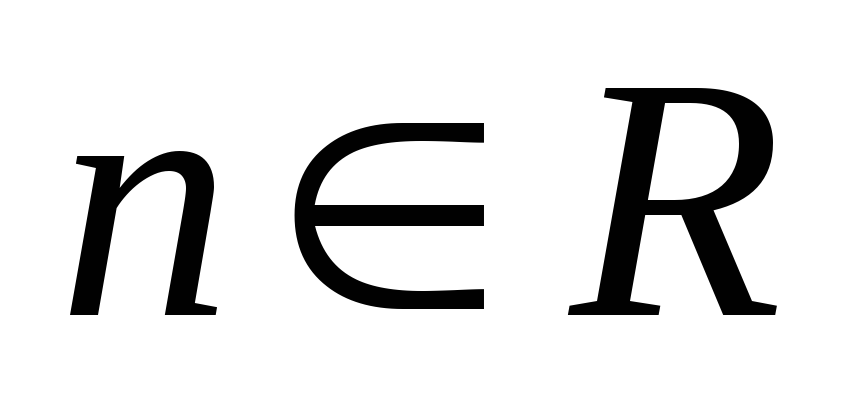2. показательная 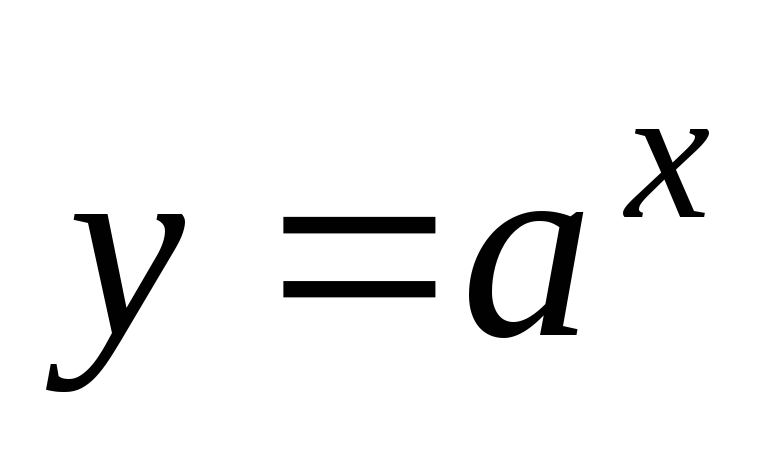, а>0, а¹1;

3. логарифмическая 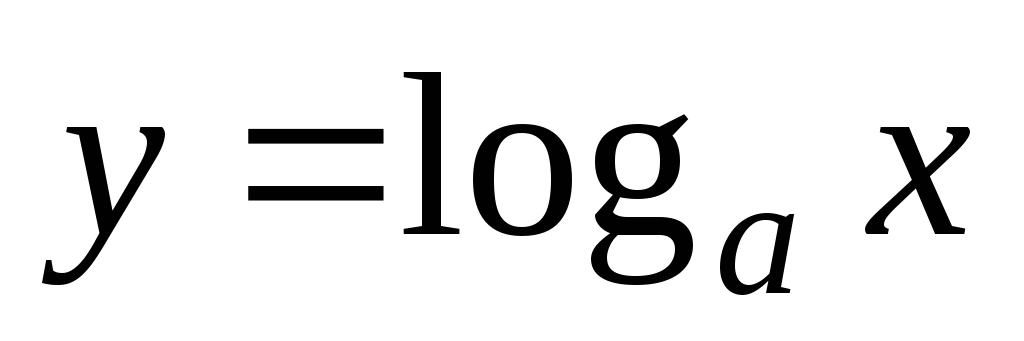, а>0, а¹1, ;

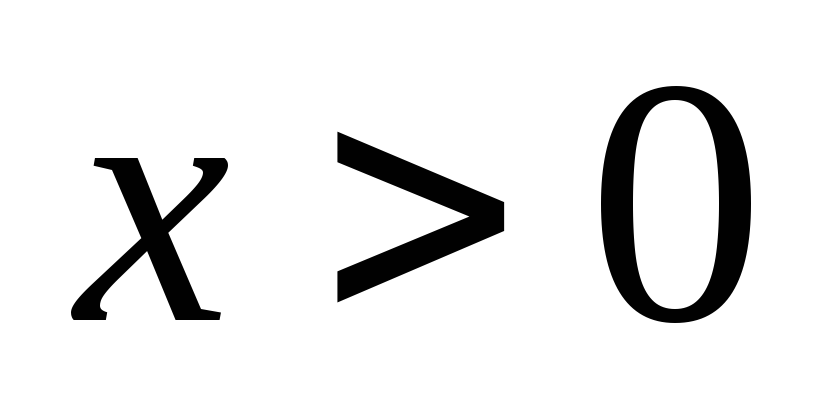4. тригонометрические: , , , ;

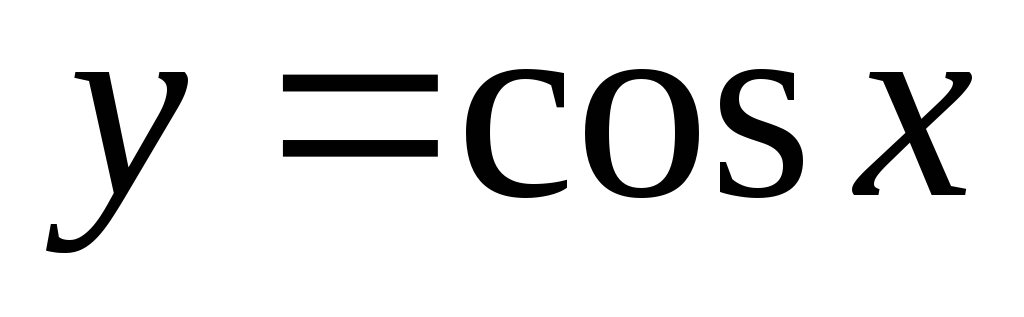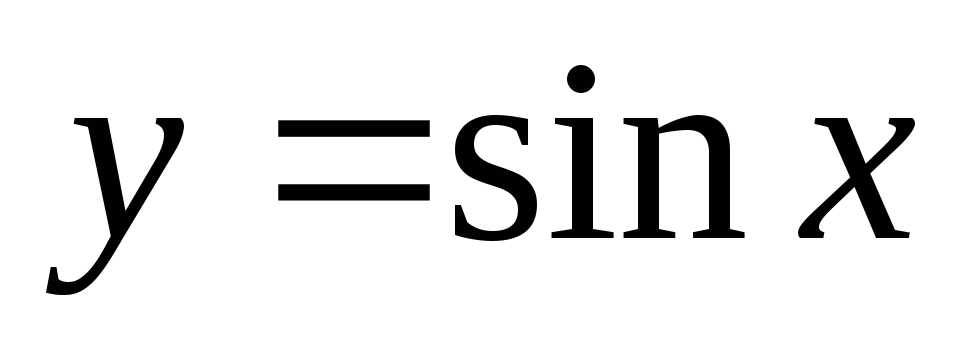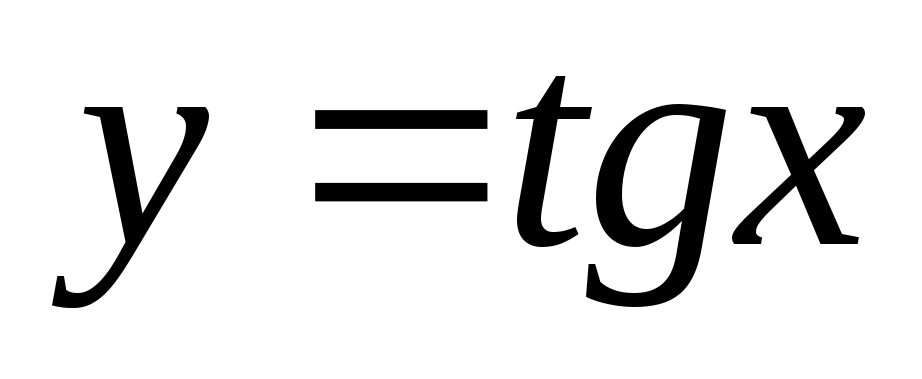5. обратные тригонометрические: , , , .

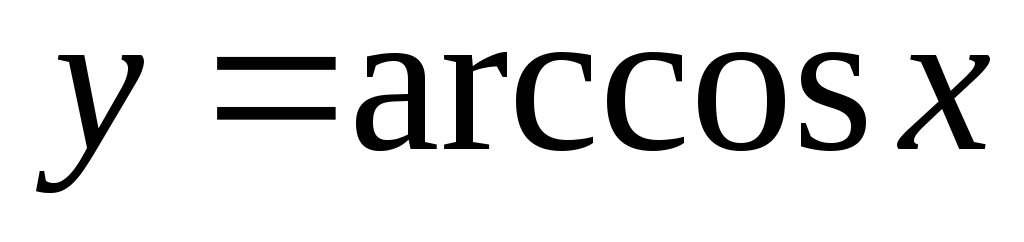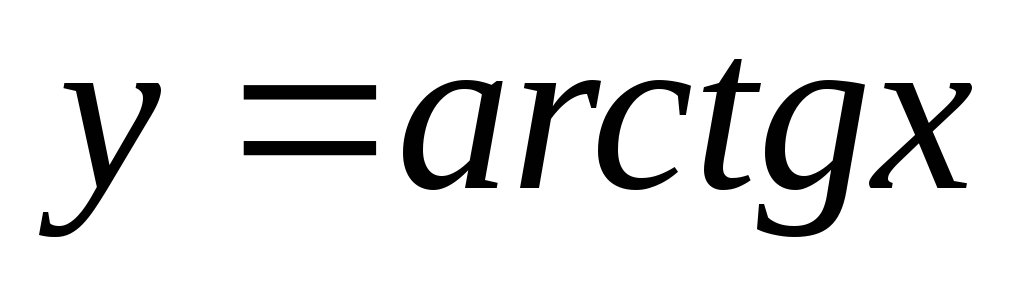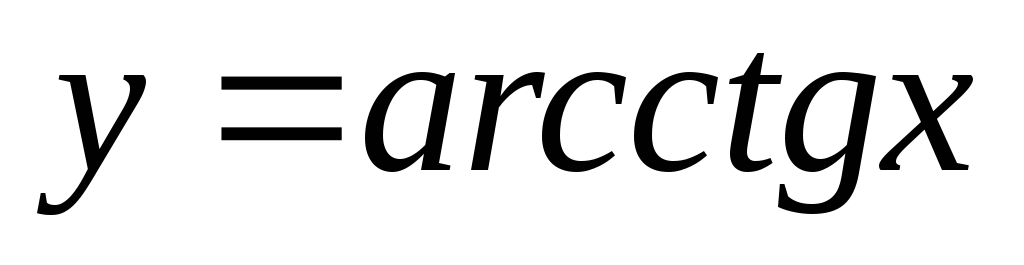Примером неэлементарной функции является

Пусть у является функцией от u, , uÎU, а u – функцией от х, , x Î X, тогда у называется сложной функцией, то есть , определенной для тех x Î X, для которых значения входят во множество U.

Например, ; – сложные функции.

Пусть функция определена на симметричном интервале относительно начала координат, то есть .

Определение. Функция называется четной, если она не изменяет свое значение при изменении знака аргумента, т. е. . Функция называется нечетной, если при изменении знака аргумента знак функции меняется, то есть .

Замечание. Отметим, что график четной функции симметри-чен относительно оси Оу, а нечетной – относительно начала координат.

Определение. Функция , , называется периодичес-кой, если существует число такое, что , . Наименьшее число T называется периодом (основным периодом).

Задание функций в полярной системе координат

Зададим на плоскости точку O, которую назовем полюсом. Проведем из полюса направленную полупрямую, которую назо-вем полярной осью.

Пусть M – произвольная точка плоскости. Соединим точку M с полюсом. Длина отрезка OM равна r и называется полярным радиусом, а угол j, откладываемый от полярной оси к отрезку OM против движения часовой стрелки, – полярным углом (рис. 8.2).

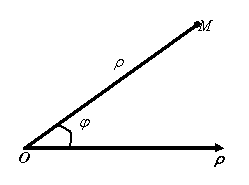
Рис. 8.2

Таким образом, положение точки М на плоскости опреде-ляется двумя координатами r и j, причем r – всегда величина неотрицательная, а угол j может принимать значения от 0 до 2π, то есть , .

Связь между полярными и декартовыми координатами

Если совместить полюс с началом координат декартовой системы (рис. 8.3), а полярную ось – с осью абсцисс, тогда пря-моугольные координаты и связаны с полярными коор-динатами r и j формулами:

, , (14)

а полярные координаты – с декартовыми формулами:

, . (15)

Замечание. При нахождении полярного угла точки, опреде-ленной в декартовой системе координат, полезно использовать следующие из формулы (15):

, , (15’)

которые позволяют определить угол с точностью до четверти.

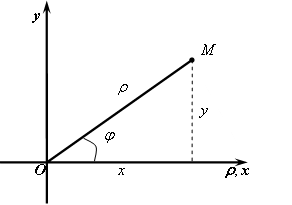
Рис. 8.3

Пример 8.2. Задана функция в полярной системе коор-динат своим уравнением . Необходимо:

1. определить точки, лежащие на линии, давая значе-ния через промежуток, равный 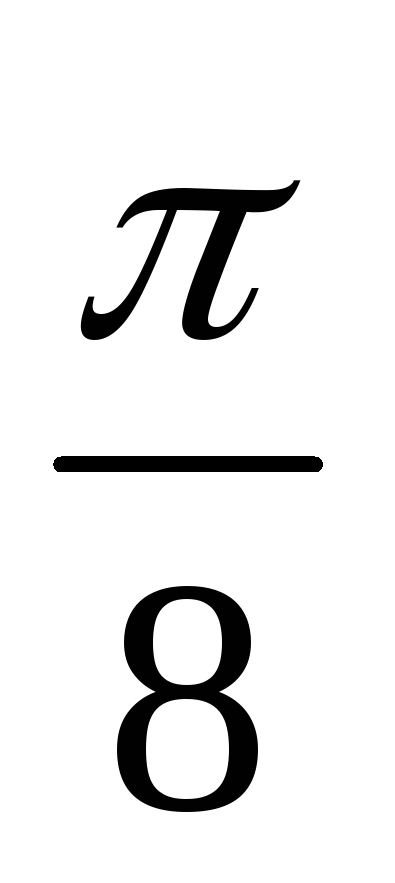, начиная от 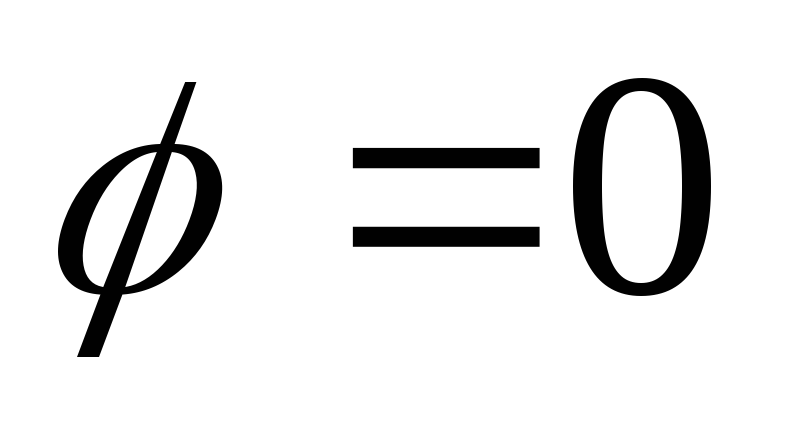и до ;

2. построить линию, соединив полученные точки;

3. найти уравнение этой линии в прямоугольной декартовой системе координат.

Решение. Придавая углу j значения с шагом , считаем значения r.

j	0
r	0	0,06	0,3	0,62	1	1,38	1,7	1,94

j	p
r	2	1,94	1,7	1,38	1	0,62	0,3	0,06

Для построения графика в полярной системе координат от-кладываем полярную ось, затем отмечаем значения углов j и на этих лучах откладываем значения полярных радиусов, соответ-ствующих данным полярным углам. Соединяем полученные точ-ки. График данной функции построен (рис. 8.4).

Рис. 8.4

Найдем задание этой линии в декартовой системе ко-ординат. Для этого воспользуемся формулами перехода (15’): . После преобразования возведем правую и левую части этого равенства в квадрат получаем уравнение линии в де-картовой системе координат .