Тема 10. Исследование функции 145

Возрастание и убывание функции 145

Экстремумы функции 146

ЗАКЛЮЧЕНИЕ 155

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 157

СПИСОК ЛИТЕРАТУРЫ 167

Нач. редакции А.С. Обвинцева 168

Введение

Кафедра высшей математики Кемеровского технологического института пищевой промышленности предлагает курс математики, соответствующий программе для вузов, общим объемом 500–700 часов, адаптированный для студентов заочного обучения.

Курс состоит из четырех частей, каждая из которых рассчитана на один семестр и включает разделы математики, соответствующие программе семестра. Каждая часть является методическим комплексом, ориентированным на самостоятельное изучение материала соответствую-щих разделов математики. Представленный материал содержит инфор-мацию, достаточную для изучения и усвоения материала, используемого в инженерных приложениях.

Настоящий методический комплекс предназначен для студентов всех специальностей заочной формы обучения, в том числе с применением дистанционных технологий.

Программа 1-го семестра включает следующие разделы: матрицы и действия над ними; определители матриц и их свой-ства; системы линейных алгебраических уравнений и способы их решения; линейные пространства; векторы и операции над ними; уравнения плоскости и прямой в пространстве; кривые второго порядка на плоскости; функции, способы их задания; пределы последовательностей и функций; непрерывность функ-ции и классификация точек разрыва; дифференцирование функ-ций; полное исследование функции и построение ее графика.

Итогом изучения семестрового курса математики является выполнение двух контрольных работ и получение зачета. Подготовиться к зачету помогут задания теста, приведенные в конце настоящего методического комплекса.

Тема 1. Элементы линейной алгебры Матрицы и действия над ними

Определение. Матрицей размера m´n называется совокуп-ность m×n элементов, представленная в виде таблицы, состоящей из m строк и n столбцов:

,

где – элемент матрицы A, стоящий на пересечении i-й строки и j-го столбца, , .

Матрица размера 1´n или m´1 называется матрицей-строкой или матрицей-столбцом соответственно (или вектором).

Если число строк матрицы равно числу столбцов, то матрица называется квадратной, а число строк называется ее порядком или размером. Матрица A порядка n имеет вид:

.

Элементы квадратной матрицы размера n, стоящие на пересечении строк и столбцов с одинаковыми номерами, то есть а₁₁, , …, , образуют главную диагональ, а сумма элементов главной диагонали называется следом матрицы. Соответственно элементы , …, , лежащие на прямой, соединяющей правый верхний и левый нижний углы матрицы, образуют побочную диагональ.

Мы будем рассматривать числовые и функциональные матрицы.

Определение. Матрица, все элементы которой равны ну-лю, называется нулевой.

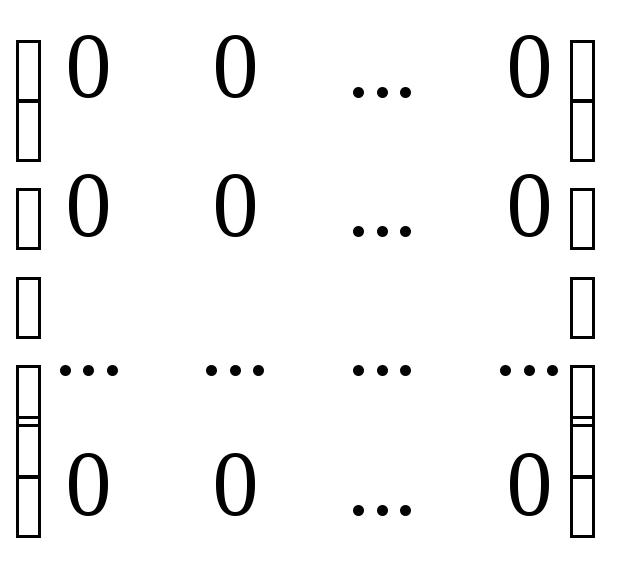
Определение. Квадратная матрица, у которой на главной диагонали стоят единицы, а остальные элементы равны нулю, называется единичной и обозначается

.

Определение. Квадратная матрица, у которой элементы, расположенные ниже главной диагонали, равны нулю, называ-ется треугольной.

Определение. Матрица А^Т называется транспонированной к матрице A, если у нее каждая строка является столбцом матрицы A с тем же номером.