Способы задания функции

Чтобы задать функцию , необходимо указать правило, позволяющее по известному значению x находить соответствующее значение y.

Наиболее популярные следующие способы задания функции.

1. Табличный. При табличном задании просто выписы-вается ряд значений независимой переменной и соответствую-щие им значения функции.

Табличный способ задания функций особенно распространен в естествознании и технике. Например, при изучении зависимости электрического сопротивления r некоторого медного стержня от тем-пературы t была получена следующая таблица:

t	19,1	25,0	30,1	36,0	40,0	45,1	50,0
r	76,30	77,80	79,75	80,80	82,35	83,90	85,10

2. Аналитический. Аналитическое задание функции сос-тоит в том, что дается формула, с помощью которой по задан-ным значениям независимой переменной можно получать соот-ветствующие им значения функции.

Например, или – формулы, которые определяют y как функцию от х.

В свою очередь аналитическое задание функции бывает явное, неявное, параметрическое и др.

Определение. Функция, заданная формулой (аналитически) вида , то есть разрешенной относительно зависимой переменной, называется явной.

Рассмотрим функцию . Здесь y однозначно не выражается через x, это неявная функция. Графиком этой функции является окружность с центром в точке и радиусом .

Определение. Функция, заданная уравнением , не разрешенным относительно зависимой переменной, называется неявной функцией.

Неявная функция может быть как однозначной, так и многозначной. Например, функция является однозначной неявной функцией.

Для доказательства существования неявной функции следует доказать, что существует решение этого уравнения, то есть найти функцию , такую, что вы-полняется равенство , .

Определение. Функция задана параметрически, если соответствующие значения x и y выражены через третью переменную t, называемую параметром, то есть .

Например, – уравнение окружности радиуса а.

3. Графический

Определение. Графиком функции называется множество всех точек плоскости, абсциссы которых являются значениями независимой переменной х, а ординаты – соответствующими значениями функции Равенство называется уравнением этого графика [3].

Функция задана графически, если начерчен ее график.

Если график функции построен (рис. 8.1), то, чтобы найти значение функции , отвечающее какому-нибудь зна-чению , необходимо отложить это значение по оси абсцисс и из полученной точки восстановить перпендикуляр до пересе-чения с графиком функции. Длина этого перпендикуляра, взятая с надлежащим знаком, и равна значению функции . Например, .

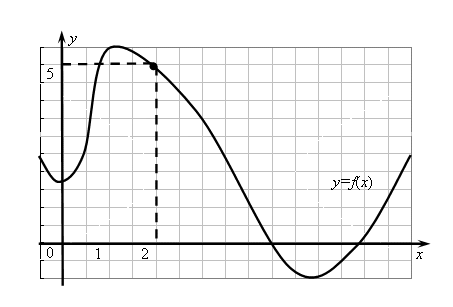
Рис. 8.1

4. Содержательный. При таком способе задания варианты независимой переменной, функции и ее значения формулируются в виде правил, законов и т. д. Например, конституция, УК и т. п.

Замечание. Представленные способы задания имеют свои достоинства и недостатки. К недостаткам табличного способа задания относится то, что, зная таблицу значений функций, не всегда можно найти аналитическое уравнение функции и соответственно значения функции в точках, не представленных в таблице. Наглядность графического способа задания оказывается неоспо-римым плюсом, к недостаткам относится неточность определяемых значений функции. Абсолютно точным способом задания функции является аналитический, так как если известно уравнение (правило) функции, то для любого возможного x всегда найдется значение y. Самый общий способ задания функции – содержательный, однако он чаще используется в гуманитарных дисциплинах и реже в математике, например, в теории вероятностей.