Деление отрезка в данном отношении

Пусть даны точки и . Требу-ется найти координаты точки , делящей отрезок прямой, заключенный между М₁ и М₂, в отношении , (рис. 7.6).

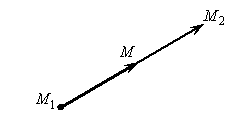
Рис. 7.6

Рассмотрим векторы

и . Они коллинеарны и одинаково направлены, то есть могут отли-чаться только длиной. По условию

,

поэтому

или в координатной форме

.

Из равенства этих двух векторов следует равенство их соот-ветствующих координат:

, ,

Отсюда

, , ,

В частности, если точка М делит отрезок М₁М₂ пополам, то и , , , то есть координаты точки, делящей отрезок пополам, равны полусуммам соответствующих координат концов отрезка.

Пример 7.12. Найти координаты точки М, делящей по-полам отрезок прямой , заключенный между плоскостями Oxz и Оxу.

Решение. Найдем точку пересечения прямой с плоскостью Oxz, полагая в уравнениях прямой . Тогда получим

или

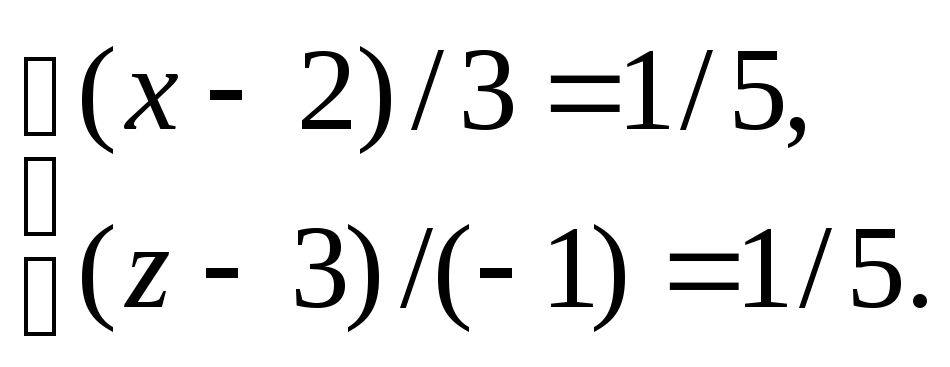
Из последней системы находим , . Эти коор-динаты вместе с определяют точку Анало-гично, полагая в уравнениях прямой , имеем: или откуда , . Получим точку пересечения прямой с плоскостью Оxу. Зная координаты концов и отрезка АВ, по формулам деления отрезка пополам определим координаты точки М – середины отрезка АВ: ; ; Итак, – искомая точка.

Пример 7.13. Даны координаты вершин пирамиды , , , . Найти: 1) длины ребер АВ и AC; 2) угол между ребрами АВ и АС; 3) площадь грани АВС; 4) объем пирамиды ABCD; 5) уравнение прямой АВ; 6) уравнение плоскости АВС; 7) уравнение высоты пирамиды, опущенной на грань АВС. Сделать чертеж.

Решение

1. Длина ребра AB совпадает с длиной вектора , поэтому определим координаты векторов и

,

.

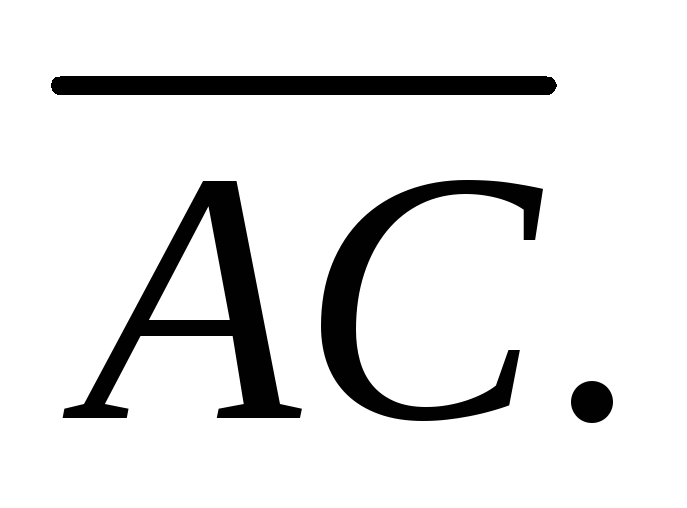
Длина вектора равна корню квадратному из суммы квадратов его координат, то есть

2. Угол между ребрами AB и AC совпадает с углом между векторам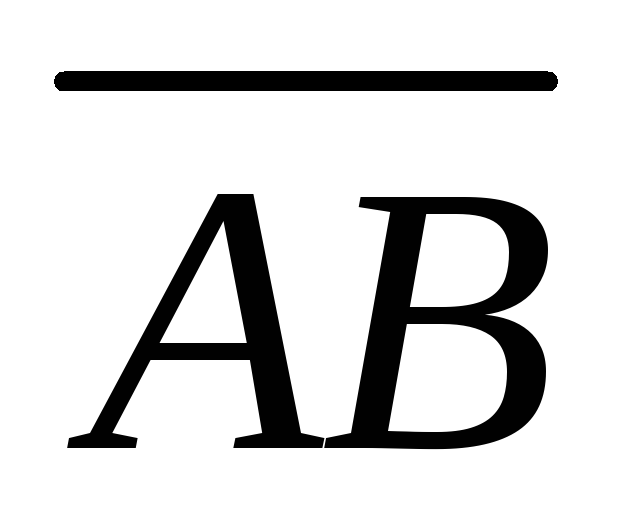и и 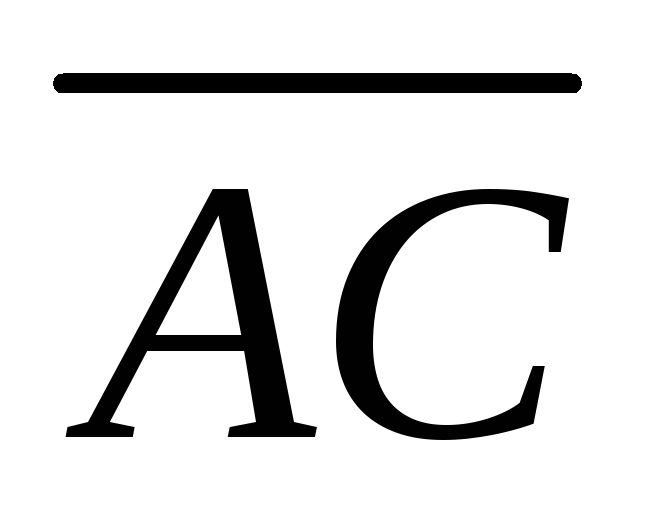, который можно определить по формуле:

, .

3. Грань ABC представляет собой треугольник, его пло-щадь найдем через векторное произведение:

так как

.

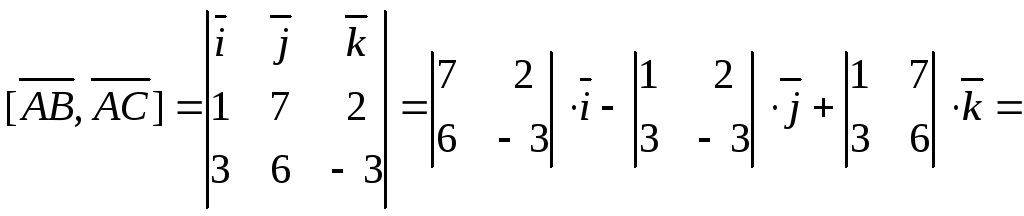
4. Объем пирамиды вычислим по формуле:

.

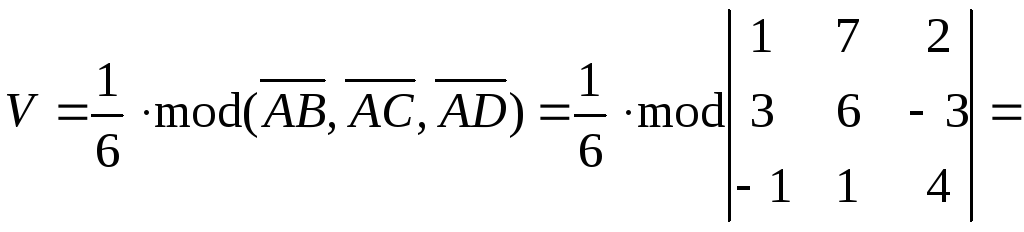
Здесь

5. Уравнение прямой, проходящей через точки А, В, имеет вид:

, то есть .

6. Уравнение плоскости ABC определим из равенства

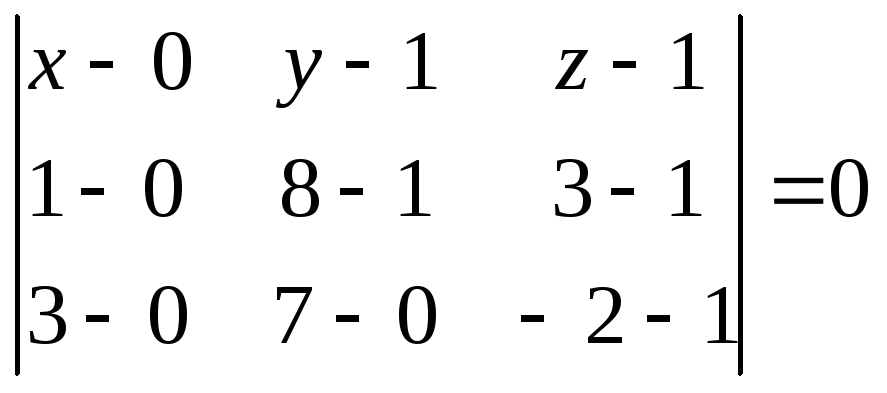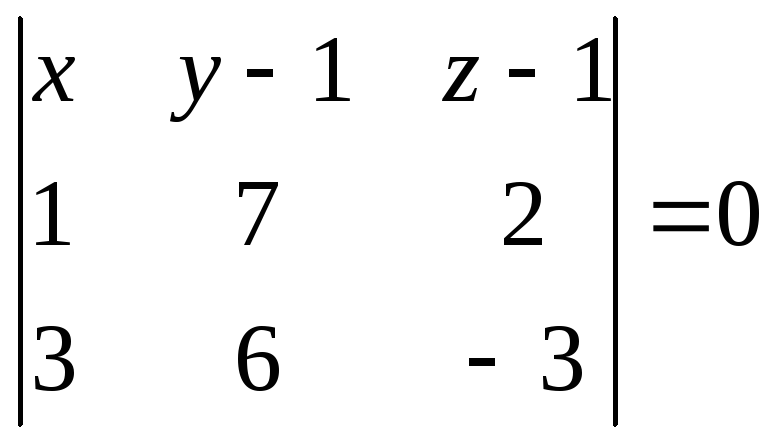, или

.

7. Так как высота – это прямая, перпендикулярная плос-кости ABC, ее направляющим вектором будет вектор-нормаль 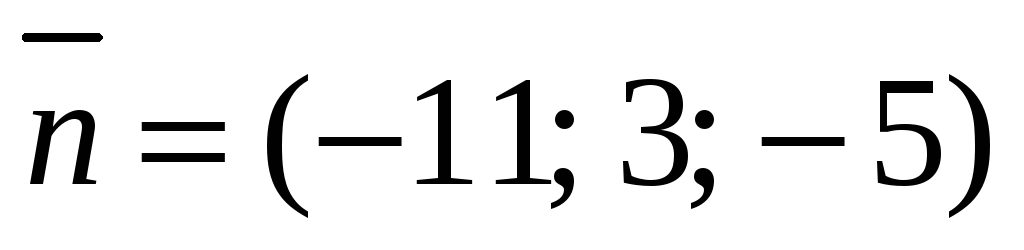плоскости ABC, тогда уравнение высоты имеет вид:

.

Выполним чертеж (рис. 7.5).

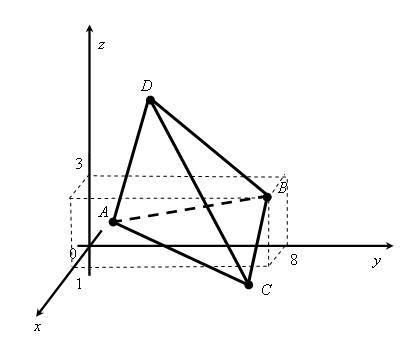
Рис. 7.5

Тема 8. Функции. Теория пределов Понятие функции

В теме 5 мы уже встречались с понятием функции, информация о которой основывалась на материале из школьного курса математики. Здесь это понятие получит свое дальнейшее развитие.

Пусть на действительной оси R заданы два числовых множества и .

Определение. Будем говорить, что на множестве X задана функция f действительной переменной x, если известен закон (отображение), по которому каждому значению по закону f ставится в соответствие единственное значение и обозначается . Переменная x называется аргументом функции f, множество X – областью определения функции, переменная y – значением функции или зависимой переменной, а множество Y – областью значений функции.

Замечание. Область Y значений функции обычно не указыва-ется, так как множество принимаемых значений функции определяет сам закон.

Допускаются многозначные функции (то есть одному x соответствует более одного значения y). Обычно эти случаи оговариваются особо.

Замечание. Для обозначения функциональной зависимос-ти вместо символа функции f можно использовать любую дру-гую букву (но не число) любого алфавита.

Определение. Совокупность всех значений независимой переменной х, для которых функция определена, назы-вается областью определения, или областью существования функции, и обозначается .

Определение. Пусть задана функция . Тогда называется значением этой функции при

Пример 8.1. Найти значения функции .

Решение. Вычислим значения функции при заданных значениях аргумента ; .