Взаимное расположение плоскостей

Пусть две плоскости заданы в общими уравнениями:

и ,

, .

Эти плоскости параллельны только в том случае, если колли­неарны их нормальные векторы и , то есть выполняются условия: .

Следовательно, две плоскости, заданные общими уравне­ниями, параллельны, если коэффициенты при одноименных пе­ременных пропорциональны.

Если кроме коэффициентов при переменных пропорцио­нальны и свободные члены, то есть выполняются равенства

,

то плоскости совпадают.

Чтобы две плоскости пересекались, необходимо и достаточно, чтобы коэффициенты при переменных x, y, z не были пропорциональны.

Плоскости перпендикулярны в том случае, если перпендикулярны их нормальные векторы, то есть выполняется условие:

.

Пример 7.5. Установить, перпендикулярны ли плоскости, заданные уравнениями и .

Решение. Плоскости перпендикулярны в том случае, если их нормальные векторы и удовлетворяют условию . Так как , то указанное условие выполнено, поэтому данные плоскости перпендикулярны.

Уравнение прямой в пространстве

Каноническое уравнение прямой. Положение прямой вполне определено, если заданы лежащая на ней точка и направление. Направление прямой может быть задано любым вектором, коллинеарным данной прямой, который называется направляющим вектором.

Выведем уравнение прямой a, проходящей через данную точку и имеющей направляющий вектор

Произвольная точка лежит на прямой a только в том случае, если векторы и коллинеарны, то есть для них выполняется условие:

.

Эти равенства (а этими равенствами фактически заданы два независимых уравнения) определяют прямую (рис. 7.4), проходящую через заданную точку коллинеарно вектору , и называются каноническим уравнением прямой в пространстве.

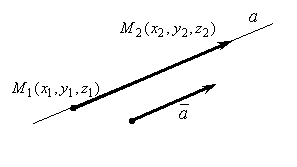
Рис. 7.4

Числа l, m и n являются проекциями направляющего вектора на координатные оси. Так как вектор – ненулевой, то все три числа l, m и n не могут одновременно равняться нулю. Но одно или два из них могут оказаться равными нулю, например,

Эта запись означает, что проекции вектора на оси Oy и Oz равны нулю. Поэтому и вектор , и прямая, заданная указанным образом, перпендикулярны осям Oy и Oz, то есть плоскости Оyz.

Пример 7.6. Составить уравнение прямой, перпендикуляр-ной плоскости и проходящей через точку пересечения этой плоскости с осью Oz.

Решение. Найдем точку пересечения данной плоскости с осью Oz. Так как любая точка, лежащая на оси Oz, имеет координаты (0; 0; z), то, полагая в заданном уравнении плоскости , получим или . Следо-вательно, точка пересечения данной плоскости с осью Oz имеет координаты (0; 0; 2). Поскольку искомая прямая перпенди-кулярна плоскости, то она параллельна ее нормальному вектору Поэтому направляющим вектором прямой может служить вектор нормали заданной плоскости.

Теперь запишем искомые уравнения прямой, проходя-щей через точку в направлении вектора

или .

Уравнения прямой, проходящей через две данные точки

Прямая может быть задана двумя лежащими на ней точками и . В этом случае направляющим вектором прямой может служить вектор , то есть . Тогда каноническое уравнение прямой в пространстве примет вид:

.

Эти равенства определяют прямую, проходящую через две данные точки.

Пример 7.7. Составить уравнения прямой, проходящей через точки и .

Решение. Запишем искомое уравнение прямой в виде:

или

.

Так как то искомая прямая перпендикулярна оси Oy.

Пример 7.8. Составить уравнение прямой, проходящей через точку параллельно прямой .

Решение. Направляющим вектором искомой прямой мо-жет служить направляющий вектор данной прямой, поскольку по условию эти прямые параллельны. Зная точку и направляющий вектор искомой прямой, запишем ее уравнение в виде:

Прямая как линия пересечения плоскостей

Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей: и , то есть как множество точек, удовлетворяющих системе двух линейных уравнений:

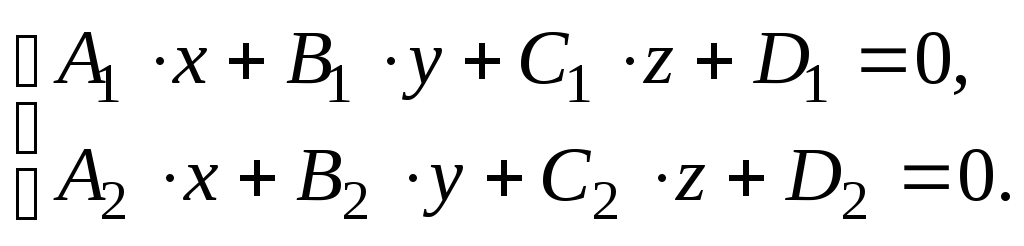(13)

Справедливо и обратное утверждение: система двух независи-мых линейных уравнений вида (13) определяет прямую как линию пересечения плоскостей (если они непараллельны). Уравнения сис-темы (13) называются общим уравнением прямой в пространстве

Пример 7.9. Составить каноническое уравнение прямой, заданной общими уравнениями плоскостей:

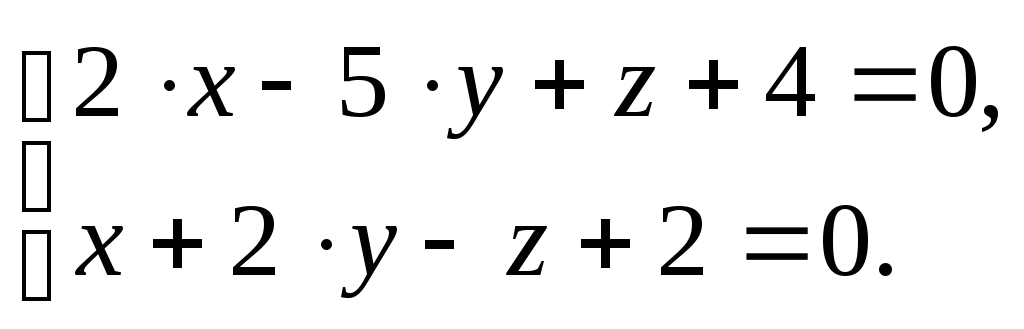
Решение. Чтобы написать каноническое уравнение прямой или, что то же самое, уравнение прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой. Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например, Oyz и Oxz.

Точка пересечения прямой с плоскостью Oyz имеет абсциссу . Поэтому, полагая в данной системе уравнений , получим систему с двумя переменными:

Ее решение , вместе с определяет точку искомой прямой. Полагая в данной системе уравнений , получим систему:

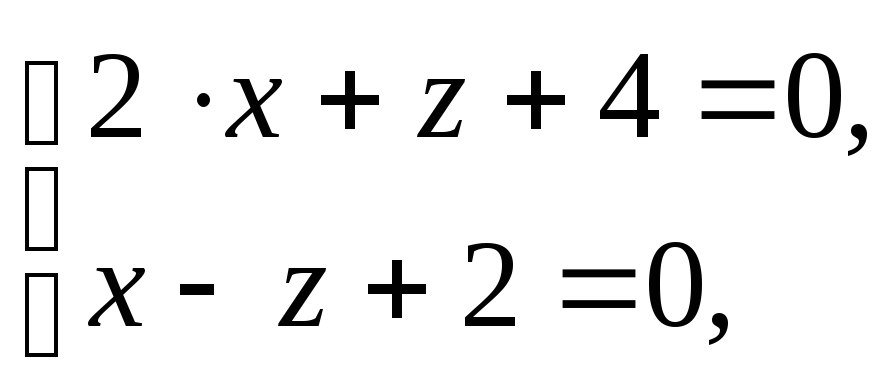
решение которой , вместе с определяет точку пересечения прямой с плоскостью Oxz.

Теперь запишем уравнения прямой, проходящей через точки и : или , где будет направляющим векто-ром этой прямой.

Пример 7.10. Прямая задана каноническим уравнением . Составить общее уравнение этой прямой.

Решение. Каноническое уравнение прямой можно запи-сать в виде системы двух независимых уравнений:

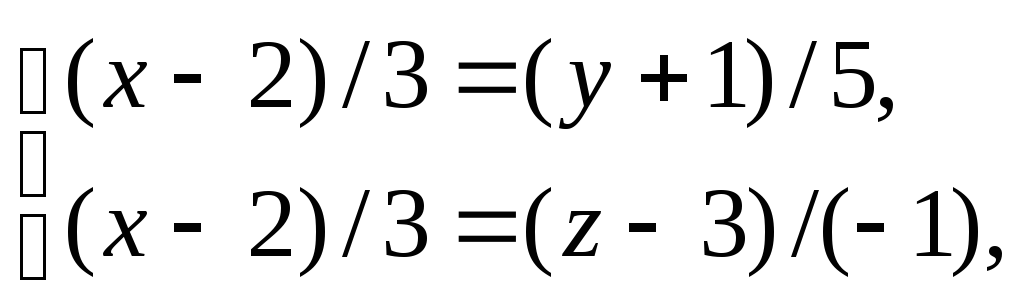Û

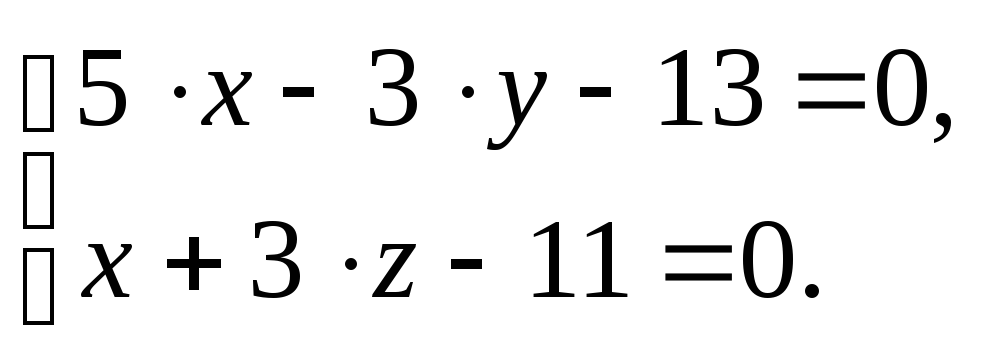
Получили общее уравнение прямой, которая теперь задана пе-ресечением двух плоскостей, одна из которых параллельна оси Oz а другая – оси Оу .

Данную прямую можно представить в виде линии пересечения двух других плоскостей, записав ее каноническое уравнение в виде другой пары независимых уравнений:

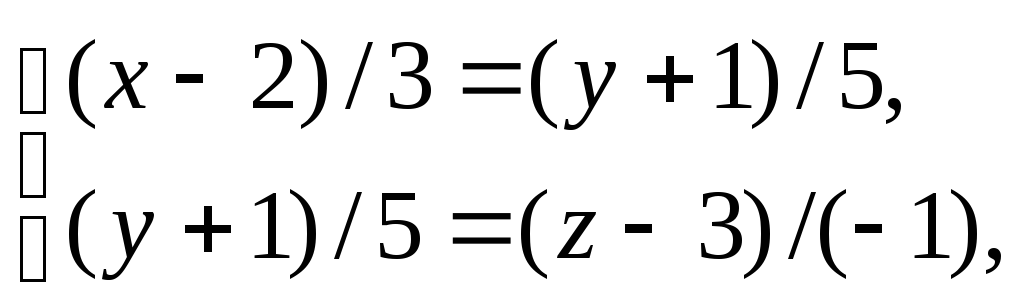Û

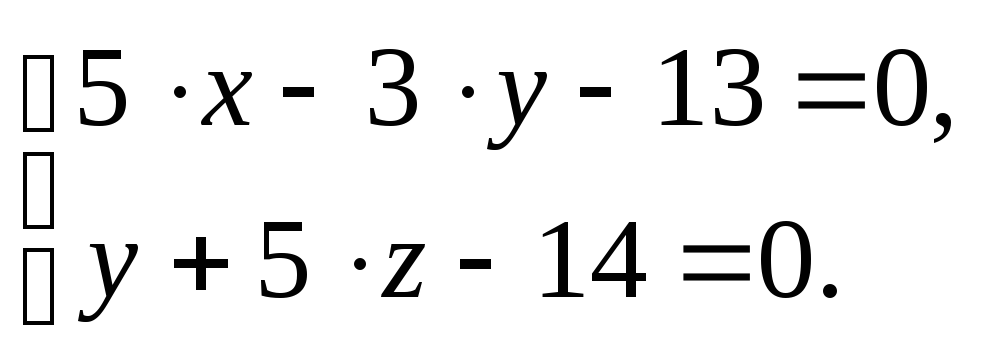
Замечание. Одна и та же прямая может быть задана различными системами двух линейных уравнений (то есть пересечением различных плоскостей, так как через одну прямую можно провести бесчисленное множество плоскостей), а также различными каноническими уравнениями (в зависимости от выбора точки на прямой и ее направляющего вектора).