
- •С.А. Иванова, в.А. Павский Математика
- •Часть 1
- •Оглавление
- •Тема 10. Исследование функции 145
- •Введение
- •Тема 1. Элементы линейной алгебры Матрицы и действия над ними
- •Действия над матрицами
- •1. Сложение матриц
- •2. Умножение матрицы на число
- •3. Умножение матриц
- •Определитель матрицы
- •Свойства определителей
- •Вычисление определителей
- •Обратная матрица
- •Ранг матрицы
- •Элементарные преобразования матрицы
- •Тема 2. Системы линейных алгебраических уравнений
- •Методы решения системы линейных алгебраических уравнений
- •1. Метод Крамера
- •2. Матричный метод
- •3. Метод Гаусса
- •Однородная система линейных алгебраических уравнений
- •Системы линейных неравенств
- •Тема 3. Линейные пространства
- •Базис линейного пространства
- •Собственные значения и собственные векторы матрицы
- •Тема 4. Элементы векторной алгебры Векторы
- •Линейные операции над векторами
- •Проекция вектора на ось
- •Разложение вектора по ортам координатных осей
- •Модуль вектора. Направляющие косинусы
- •Базис системы векторов
- •Скалярное произведение векторов
- •Cвойства скалярного произведения
- •С помощью скалярного произведения находят
- •Векторное и смешанное произведение векторов
- •Свойства векторного произведения
- •Свойства смешанного произведения
- •Тема 5. Аналитическая геометрия на плоскости Система координат на плоскости
- •Уравнение линии на плоскости
- •Уравнение прямой на плоскости
- •Тема 6. Кривые второго порядка
- •Окружность
- •Гипербола
- •Парабола
- •Тема 7. Аналитическая геометрия в пространстве Уравнение поверхности и линии в пространстве
- •Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей
- •Уравнение прямой в пространстве
- •Уравнения прямой, проходящей через две данные точки
- •Деление отрезка в данном отношении
- •Тема 8. Функции. Теория пределов Понятие функции
- •Способы задания функции
- •Графический
- •Элементарные функции
- •Задание функций в полярной системе координат
- •Числовые последовательности
- •Предел числовой последовательности
- •Свойства бесконечно малых
- •Свойства сходящихся последовательностей
- •О сжатой последовательности
- •Предел функции
- •Основные теоремы о пределах
- •Вычисление пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Эквивалентные функции
- •Непрерывность функции
- •Классификация точек разрыва
- •Тема 9. Дифференциальное исчисление Определение производной
- •Геометрический смысл производной
- •Правила дифференцирования, таблица производных
- •Правила дифференцирования
- •Производные сложной и обратной функций
- •Дифференцирование неявных и параметрически заданных функций
- •Логарифмическое дифференцирование
- •Геометрические приложения производной
- •Дифференциал функции
- •Основные свойства дифференциала
- •Производные высших порядков
- •Теоремы о дифференцируемости функции
- •Правило Лопиталя
- •Формула Тейлора
- •Тема 10. Исследование функции Возрастание и убывание функции
- •Экстремумы функции
- •Наибольшее и наименьшее значения функции
- •Вогнутость и выпуклость функции. Точки перегиба
- •Асимптоты графика функции
- •Заключение
- •Задания для самостоятельной работы
- •Список литературы
- •Математика
- •Часть 1 Нач. Редакции а.С. Обвинцева
- •650010, Г. Кемерово, ул. Красноармейская, 52
Уравнение прямой на плоскости
Общее уравнение
прямой на
плоскости
![]() имеет вид
имеет вид
![]() ,
где A,
B,
C
– произвольные числа, причем A
и B
одновременно не равны нулю. Рассмотрим
некоторые част-ные случаи прямой.
,
где A,
B,
C
– произвольные числа, причем A
и B
одновременно не равны нулю. Рассмотрим
некоторые част-ные случаи прямой.
-
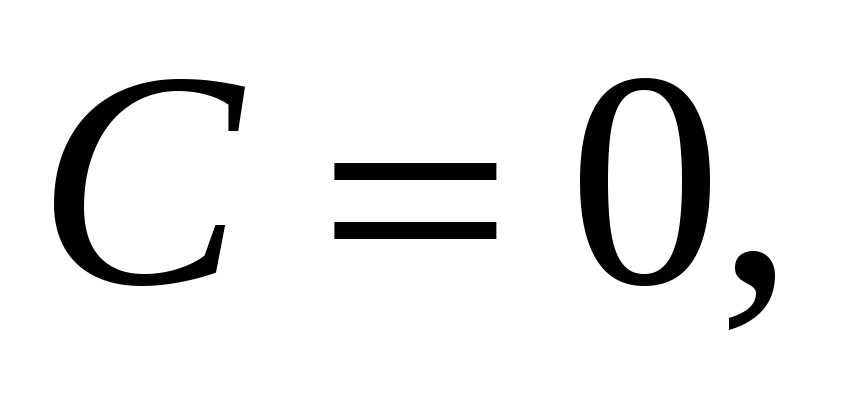 А
и B
отличны
от нуля, то прямая, определяемая
уравнением
А
и B
отличны
от нуля, то прямая, определяемая
уравнением
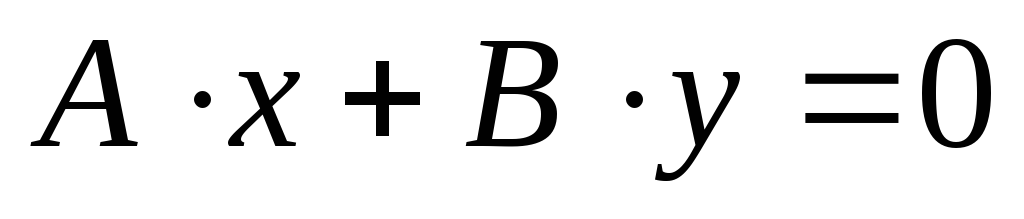 ,
проходит через начало координат.
,
проходит через начало координат. -
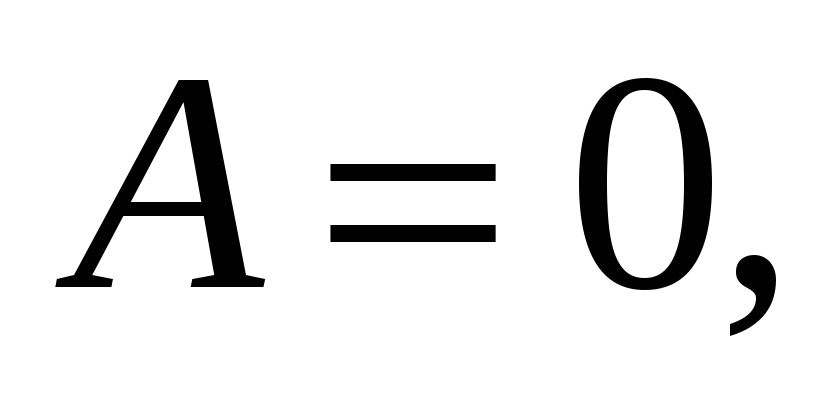 B
и
C
отличны
от нуля, то прямая, определяемая
уравнением
B
и
C
отличны
от нуля, то прямая, определяемая
уравнением
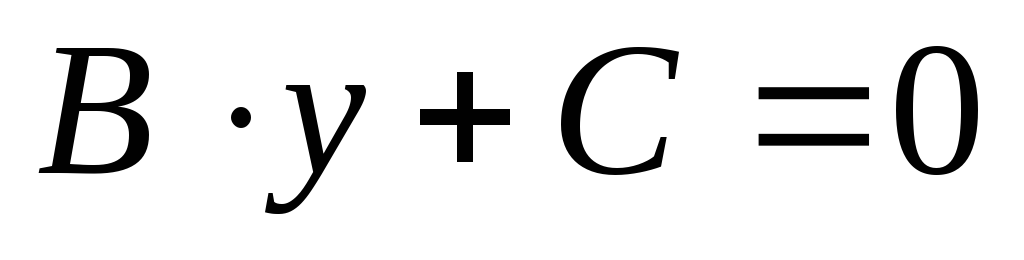 или
или
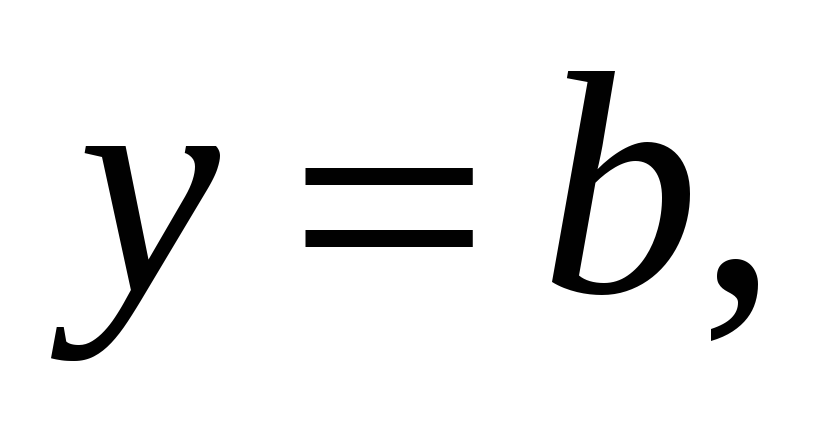 параллельна оси Ox.
параллельна оси Ox. -
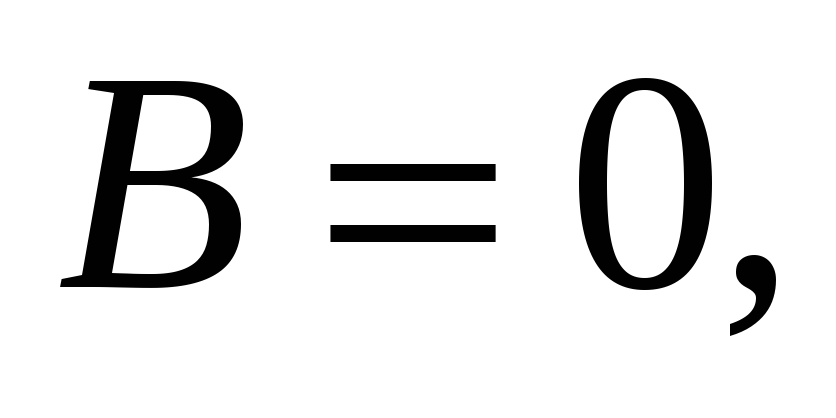 A
и
C
отличны
от нуля, то прямая, определяемая
уравнением
A
и
C
отличны
от нуля, то прямая, определяемая
уравнением
 или
или
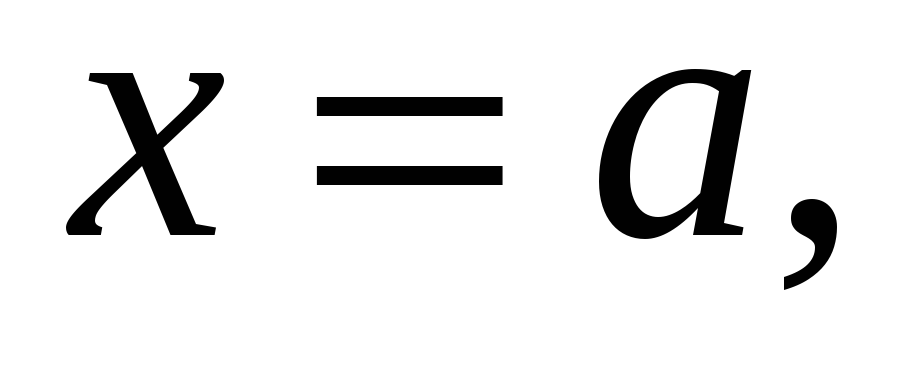 параллельна оси Оу.
параллельна оси Оу. -
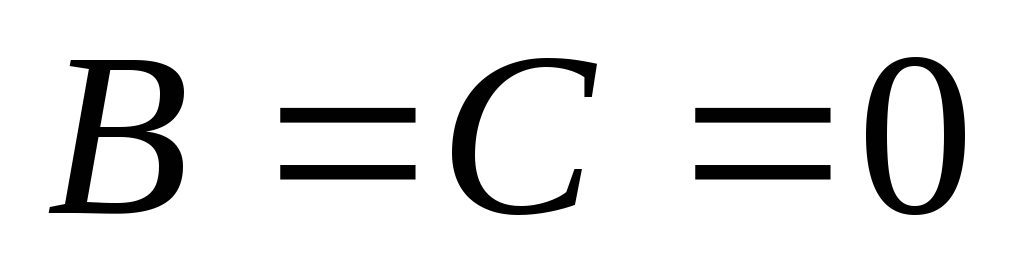 ,
,
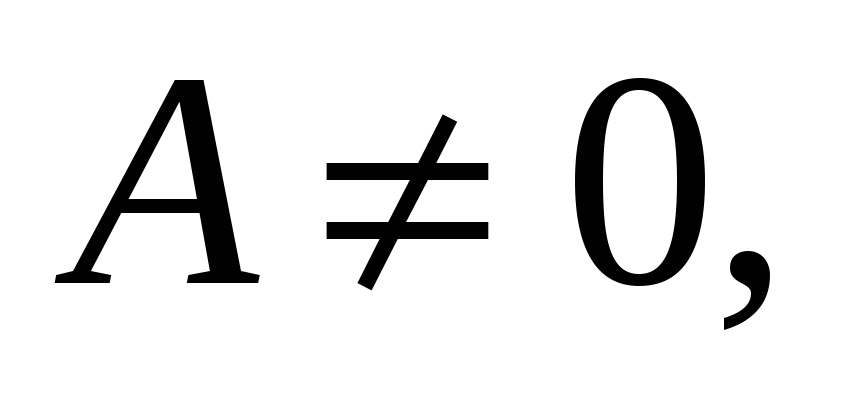 то
прямая,
определяемая уравнением
то
прямая,
определяемая уравнением
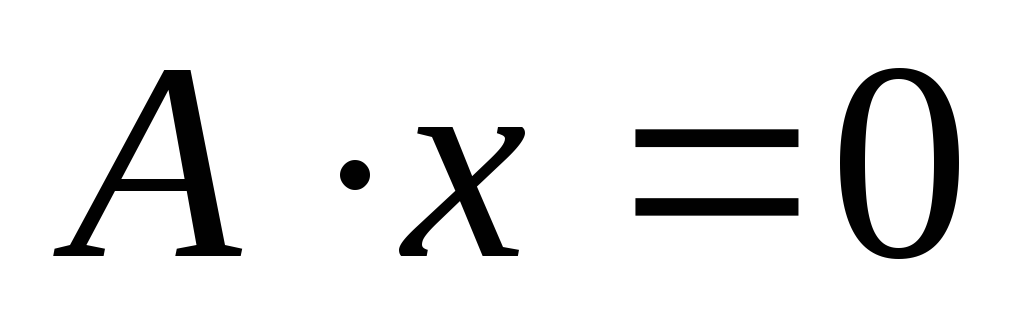 ,
совпадает
с осью Оу.
,
совпадает
с осью Оу. -
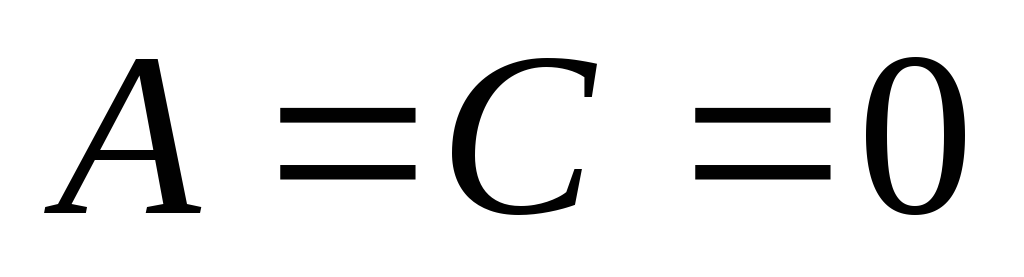 ,
,
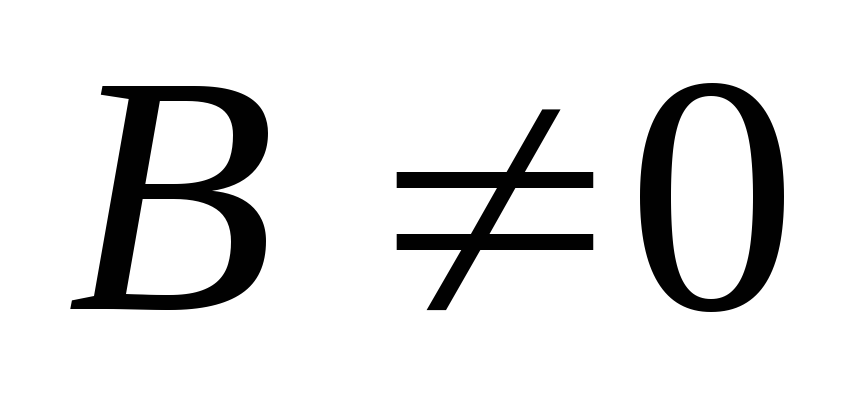 ,
то
прямая,
определяемая уравнением
,
то
прямая,
определяемая уравнением
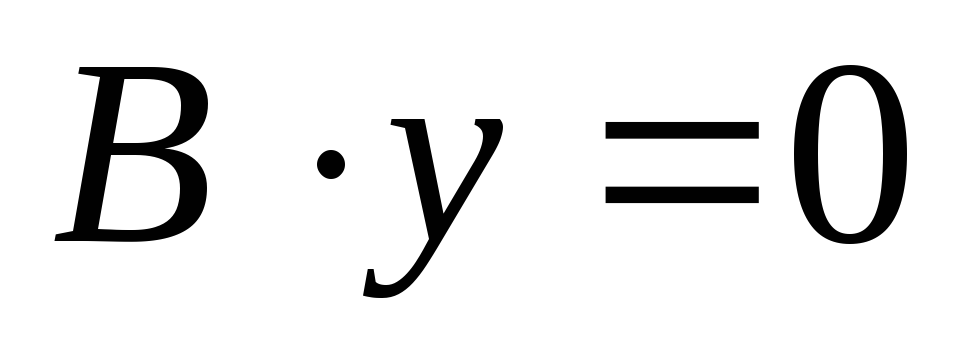 ,
совпадает
с осью Ox.
,
совпадает
с осью Ox.
Уравнение
прямой, проходящей через заданную точку
перпендикулярно
вектору.
Произвольная точка
![]() лежит на данной прямой тогда и только
тогда, когда вектор
лежит на данной прямой тогда и только
тогда, когда вектор
![]() перпендикулярен
вектору
перпендикулярен
вектору
![]() ,
и, значит, скалярное произ-ведение этих
векторов будет равно нулю:
,
и, значит, скалярное произ-ведение этих
векторов будет равно нулю:
![]() – координатная
форма уравне-ния прямой, проходящей
через заданную точку
– координатная
форма уравне-ния прямой, проходящей
через заданную точку
![]() пер-пендикулярно вектору
пер-пендикулярно вектору
![]() .
Подчеркнем, что в общем уравнении прямой
вектор, составленный из коэффициентов
.
Подчеркнем, что в общем уравнении прямой
вектор, составленный из коэффициентов
![]() определяет перпендикулярный вектор к
данной прямой.
определяет перпендикулярный вектор к
данной прямой.
Если
![]() ,
то при
,
то при
![]() ,
,
![]() общее уравне-ние прямой перепишется в
виде, разрешенном относительно y:
общее уравне-ние прямой перепишется в
виде, разрешенном относительно y:
![]() .
Получили
уравнение
прямой с угловым коэффициентом.
Величина k
равна тангенсу угла наклона прямой к
оси Ox,
а величина b
по модулю равна длине отрезка, отсекаемого
прямой на оси Оу.
.
Получили
уравнение
прямой с угловым коэффициентом.
Величина k
равна тангенсу угла наклона прямой к
оси Ox,
а величина b
по модулю равна длине отрезка, отсекаемого
прямой на оси Оу.
Уравнение
прямой, проходящей через заданную точку
параллельно заданному вектору.
Вектор
![]() ,
лежащий на исходной или параллельной
ей прямой, называется направля-ющим
вектором этой прямой.
,
лежащий на исходной или параллельной
ей прямой, называется направля-ющим
вектором этой прямой.
Произвольная
точка
![]() лежит на данной прямой тогда и только
тогда, когда вектор
лежит на данной прямой тогда и только
тогда, когда вектор
![]() параллелен век-тору
параллелен век-тору
![]() и, значит, их координаты пропорциональны,
то есть
и, значит, их координаты пропорциональны,
то есть
![]() .
(11)
.
(11)
Уравнение (11) называется каноническим уравнением прямой на плоскости.
Замечание.
Каноническая форма уравнения прямой –
символическая.
Допускается
запись, например,
![]() .
Переходя к привычной форме, будем иметь
.
Переходя к привычной форме, будем иметь
![]() ,
то есть прямая параллельна оси Ox.
,
то есть прямая параллельна оси Ox.
Теперь
предположим, что коэффициент
пропорциональности ра-вен t,
то
есть
![]() Выражая отсюда переменные
x,
y,
получим параметрическое
уравнение прямой:
Выражая отсюда переменные
x,
y,
получим параметрическое
уравнение прямой:
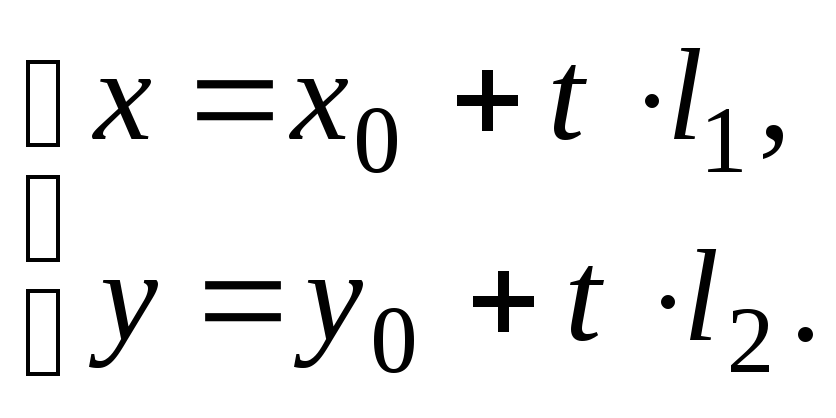
В
частности, если прямая проходит через
точки
![]() и
и
![]() то в качестве
вектора
то в качестве
вектора
![]() можно взять вектор
можно взять вектор
![]() поэтому
равенство (11) запишется в виде:
поэтому
равенство (11) запишется в виде:
![]() –
–
– уравнение прямой, проходящей через две заданные точки.
Пусть
прямая задана своим общим уравнением
![]() .
Найдем
расстояние
от точки
.
Найдем
расстояние
от точки
![]() до прямой.
Пусть
до прямой.
Пусть
![]() – произвольная
точка прямой, тогда проекция вектора
– произвольная
точка прямой, тогда проекция вектора
![]()
![]() на
вектор нормали к прямой
на
вектор нормали к прямой
![]() и будет требуемым расстоянием:
и будет требуемым расстоянием:
![]()
![]() ,
,
так как
![]() .
.
Расстояние
d
от точки
![]() до
прямой
до
прямой
![]() равно
равно
![]() .
.
Пример 5.2. Написать
уравнение прямой, проходящей через
точку
![]() параллельно оси Oy.
параллельно оси Oy.
Решение.
В качестве направляющего вектора
![]() можно взять орт
можно взять орт
![]() .
Подставив данные в каноническое уравнение
прямой (11), получим:
.
Подставив данные в каноническое уравнение
прямой (11), получим:
![]() .
От канонического уравнения прямой
обычно переходят к общему:
.
От канонического уравнения прямой
обычно переходят к общему:
![]() или
или
![]() .
.
Пример 5.3. Даны
вершины треугольника АВС:
![]() ,
,
![]()
![]() .
Найти:
1) уравнение стороны AB;
2) уравнение и
длину
высоты CD,
опущенной из вершины C
на сторону AB;
3)
уравнение медианы AE.
.
Найти:
1) уравнение стороны AB;
2) уравнение и
длину
высоты CD,
опущенной из вершины C
на сторону AB;
3)
уравнение медианы AE.
Решение.
1) Уравнение прямой AB
через две заданные точки будет иметь
вид:
![]() ;
;
![]() или
или
![]() .
.
2) Высота CD
перпендикулярна стороне AB,
а потому вектор
![]() ,
составленный из коэффициентов уравнения
прямой АВ,
перпендикулярен прямой АВ
и параллелен высоте CD.
Чтобы найти уравнение прямой CD,
подставим в уравнение (11) координаты
точки
,
составленный из коэффициентов уравнения
прямой АВ,
перпендикулярен прямой АВ
и параллелен высоте CD.
Чтобы найти уравнение прямой CD,
подставим в уравнение (11) координаты
точки
![]() и направляющего вектора
и направляющего вектора
![]() :
:
![]() или
или
![]() .
.
Длину высоты найдем
по формуле расстояния от точки
![]() до прямой AB
(
до прямой AB
(![]() ):
):
![]()
3) Определим
координаты точки E
с помощью формул деления отрезка пополам
[2]:
![]() ,
,
![]() .
Используя координаты вершин B
и C,
получаем:
.
Используя координаты вершин B
и C,
получаем:
![]() ;
;
![]() ;
;
![]()
По
точкам A
и E
построим уравнение медианы
![]() ,
после упрощения которого получим
,
после упрощения которого получим
![]() .
.
