Тема 5. Аналитическая геометрия на плоскости Система координат на плоскости

Аналитическая геометрия – раздел геометрии, изучающий геометрические образы алгебраическими средствами, основыва-ющимися на методе координат.

Под системой координат на плоскости понимают пра-вило, устанавливающее взаимно однозначное соотношение меж-ду точками плоскости и упорядоченными парами чисел, кото-рые называют координатами исходной точки.

Проведем через фиксированную на плоскости точку O две несовпадающие прямые с заданными направлениями и единич-ными отрезками. Если прямые пересекаются под прямым углом, то введенная система координат называется декартовой, или прямоугольной, в противном случае – аффинной, или косо-угольной. Первая координата точки в такой системе координат называется абсциссой, вторая – ординатой. Точка пересечения координатных осей называется началом координат.

В декартовой системе координат обычно горизонтальную ось Ox называют осью абсцисс, Oy – осью ординат.

Рассмотрим точку M на плоскости Oxy (рис. 5.1). Вектор называется радиус-вектором точки М. Чтобы найти ее коор-динаты, неодходимо из этой точки опустить перпендикуляры на каждую из осей. Числа, соответствующие полученным точкам пересечения, и будут координатами точки . Если точка лежит на оси Ox, то ее вторая координата равна 0, если на оси Oy, то – первая.

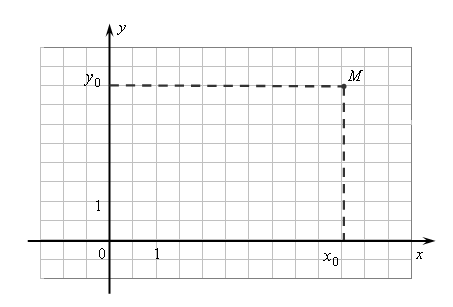
Рис. 5.1

Другой практически важной системой координат является полярная. Полярная система координат задается точкой, назы-ваемой полюсом, лучом Or, называемым полярной осью, и еди-ничным вектором того же направления, что и луч Or. Положение произвольной точки М на плоскости определяется двумя числами: ее расстоянием r от полюса и углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки). Числа r и φ называются полярными координатами точки М, пишут , при этом r называют полярным радиусом,  – полярным углом. Более подробно полярную систему координат рассмотрим в теме 8.

Уравнение линии на плоскости

Уравнение линии на плоскости задается равенствами: а) в неявном виде , б) в разрешенном, относительно y: , которым удовлетворяют координаты х и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Переменные х и y в уравнении линии называются текущими координатами точек линии.

Пример 5.1. Лежат ли точки и на линии ?

Решение. Подставим координаты точки М в уравнение линии: – значит точка М не лежит на заданной линии; теперь подставим координаты точки K в уравнение линии: – координаты этой точки удовлетворяют уравнению линии, поэтому точка K лежит на заданной прямой.

Задача о нахождении точек пересечения двух линий, за-данных уравнениями и , сводится к поиску то-чек, координаты которых удовлетворяют уравнениям обеих ли-ний, то есть сводится к решению системы двух уравнений с дву-мя неизвестными:

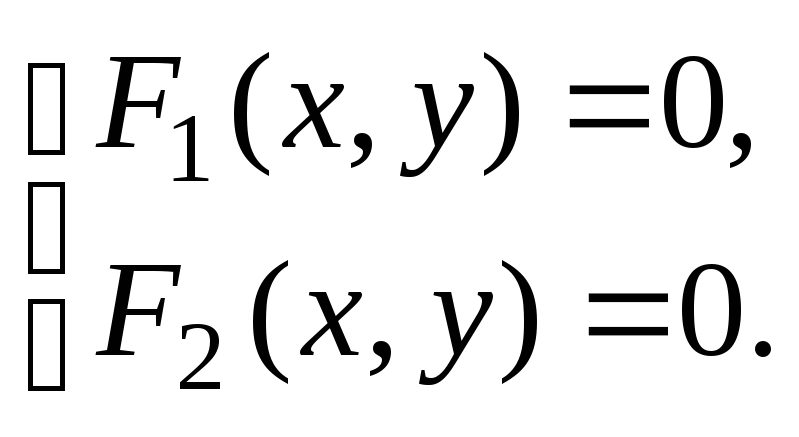
Если эта система не имеет действительных корней, то ли-нии не пересекаются.

Аналогичным образом вводится понятие линии в поляр-ной системе координат. Уравнение называется урав-нением данной линии в полярной системе координат, если ко-ординаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.

Линию на плоскости можно задать при помощи двух уравнений:

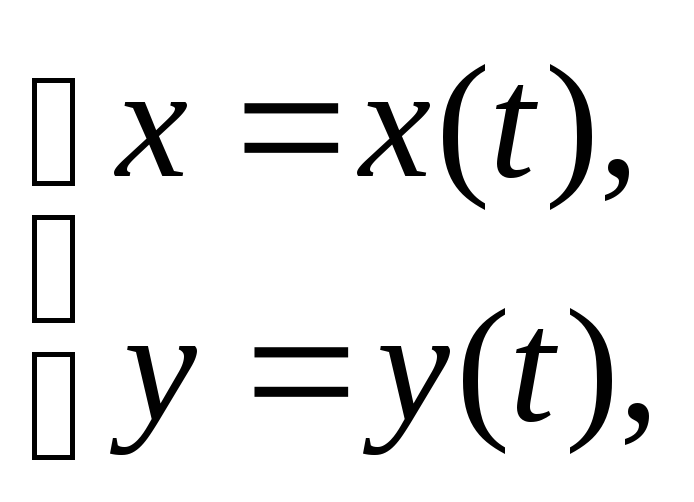
где х, у – координаты произвольной точки , лежащей на данной линии, а t – переменная, называемая параметром линии. Такой способ задания линии называется параметрическим. Более подробно задание функции параметрически и в полярной системе координат рассматривается в теме 8.

Линию на плоскости можно задать и векторным уравне-нием , где t – скалярный переменный параметр. Каж-дому значению соответствует определенный вектор на плоскости. При изменении параметра t конец вектора опишет некоторую линию.

Векторное и параметрическое уравнения имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения, а линия – траекторией точки, параметр t при этом интерпретируется как время.

В аналитической геометрии на плоскости возникают две основные задачи: зная геометрические свойства кривой, найти ее уравнение и, зная уравнение кривой, изучить ее форму и свойства [2].