
- •С.А. Иванова, в.А. Павский Математика
- •Часть 1
- •Оглавление
- •Тема 10. Исследование функции 145
- •Введение
- •Тема 1. Элементы линейной алгебры Матрицы и действия над ними
- •Действия над матрицами
- •1. Сложение матриц
- •2. Умножение матрицы на число
- •3. Умножение матриц
- •Определитель матрицы
- •Свойства определителей
- •Вычисление определителей
- •Обратная матрица
- •Ранг матрицы
- •Элементарные преобразования матрицы
- •Тема 2. Системы линейных алгебраических уравнений
- •Методы решения системы линейных алгебраических уравнений
- •1. Метод Крамера
- •2. Матричный метод
- •3. Метод Гаусса
- •Однородная система линейных алгебраических уравнений
- •Системы линейных неравенств
- •Тема 3. Линейные пространства
- •Базис линейного пространства
- •Собственные значения и собственные векторы матрицы
- •Тема 4. Элементы векторной алгебры Векторы
- •Линейные операции над векторами
- •Проекция вектора на ось
- •Разложение вектора по ортам координатных осей
- •Модуль вектора. Направляющие косинусы
- •Базис системы векторов
- •Скалярное произведение векторов
- •Cвойства скалярного произведения
- •С помощью скалярного произведения находят
- •Векторное и смешанное произведение векторов
- •Свойства векторного произведения
- •Свойства смешанного произведения
- •Тема 5. Аналитическая геометрия на плоскости Система координат на плоскости
- •Уравнение линии на плоскости
- •Уравнение прямой на плоскости
- •Тема 6. Кривые второго порядка
- •Окружность
- •Гипербола
- •Парабола
- •Тема 7. Аналитическая геометрия в пространстве Уравнение поверхности и линии в пространстве
- •Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей
- •Уравнение прямой в пространстве
- •Уравнения прямой, проходящей через две данные точки
- •Деление отрезка в данном отношении
- •Тема 8. Функции. Теория пределов Понятие функции
- •Способы задания функции
- •Графический
- •Элементарные функции
- •Задание функций в полярной системе координат
- •Числовые последовательности
- •Предел числовой последовательности
- •Свойства бесконечно малых
- •Свойства сходящихся последовательностей
- •О сжатой последовательности
- •Предел функции
- •Основные теоремы о пределах
- •Вычисление пределов
- •Первый замечательный предел
- •Второй замечательный предел
- •Эквивалентные функции
- •Непрерывность функции
- •Классификация точек разрыва
- •Тема 9. Дифференциальное исчисление Определение производной
- •Геометрический смысл производной
- •Правила дифференцирования, таблица производных
- •Правила дифференцирования
- •Производные сложной и обратной функций
- •Дифференцирование неявных и параметрически заданных функций
- •Логарифмическое дифференцирование
- •Геометрические приложения производной
- •Дифференциал функции
- •Основные свойства дифференциала
- •Производные высших порядков
- •Теоремы о дифференцируемости функции
- •Правило Лопиталя
- •Формула Тейлора
- •Тема 10. Исследование функции Возрастание и убывание функции
- •Экстремумы функции
- •Наибольшее и наименьшее значения функции
- •Вогнутость и выпуклость функции. Точки перегиба
- •Асимптоты графика функции
- •Заключение
- •Задания для самостоятельной работы
- •Список литературы
- •Математика
- •Часть 1 Нач. Редакции а.С. Обвинцева
- •650010, Г. Кемерово, ул. Красноармейская, 52
Cвойства скалярного произведения
-
 ;
; -
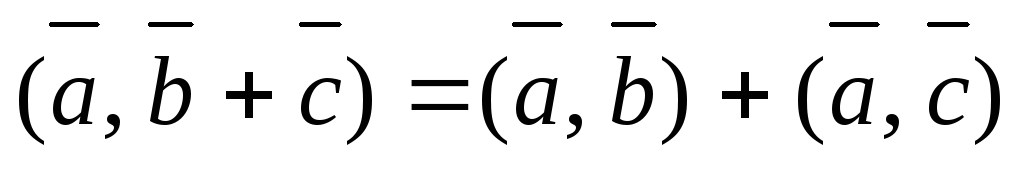 ;
; -
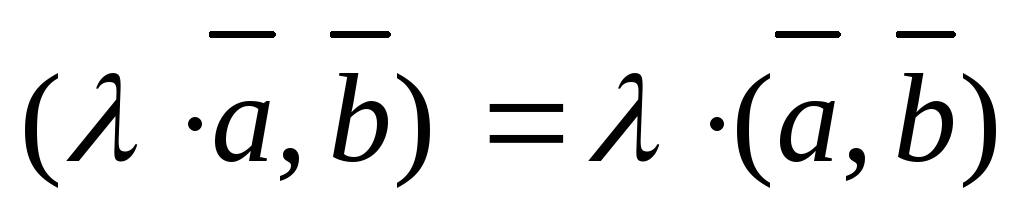 ;
; -
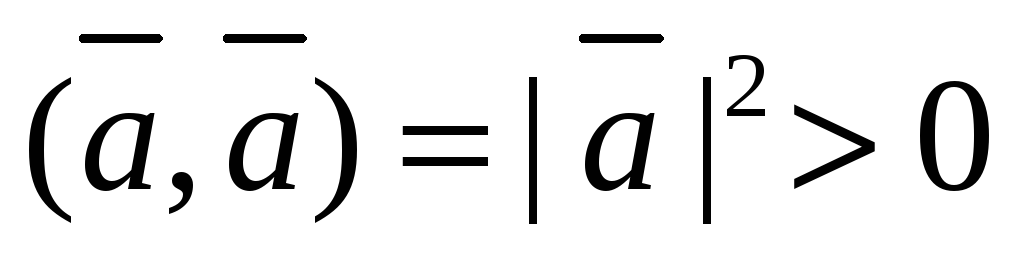 при
при
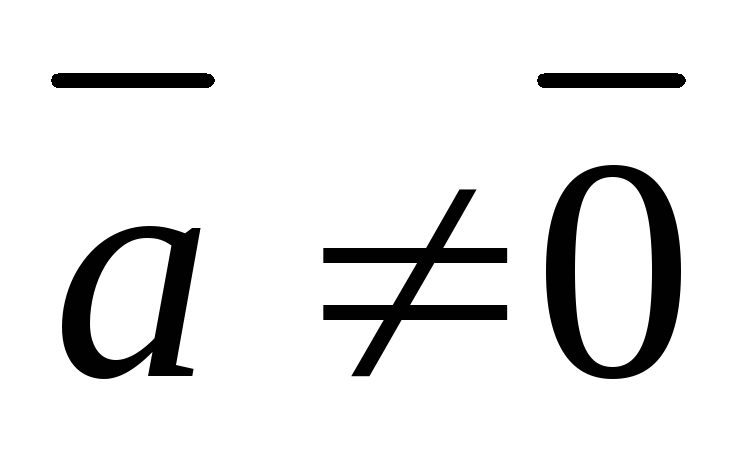 ;
; -
скалярное произведение двух векторов, заданных де-картовыми прямоугольными координатами, равно сумме про-изведений одноименных декартовых координат, то есть если
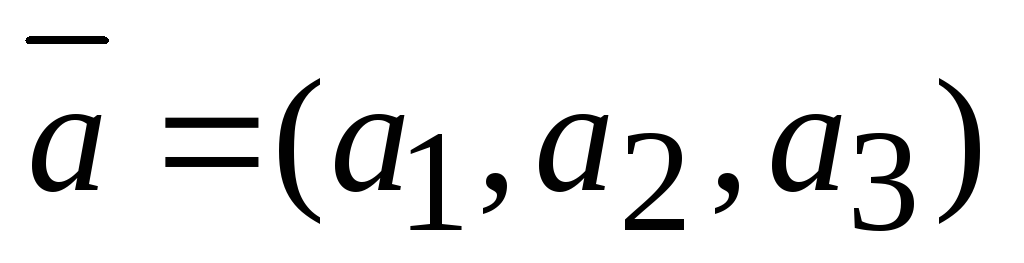 и
и
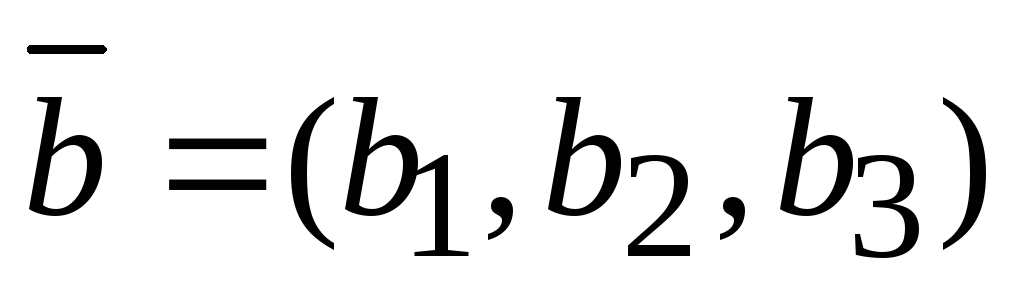 ,
то
,
то
![]() .
.
Действительно,
так как
![]() ,
,
![]() ,
,
![]() – единичные и ортогональные меж-ду
собой векторы, тогда
– единичные и ортогональные меж-ду
собой векторы, тогда
![]() ,
,
![]() и
по свойствам 1–4 скалярного произведения
получаем:
и
по свойствам 1–4 скалярного произведения
получаем:
![]()
![]()
![]()
![]()
![]()
![]()
Замечание. Свойство 5 в прямоугольной системе координат можно принять за определение скалярного произведения.
С помощью скалярного произведения находят
-
длину вектора
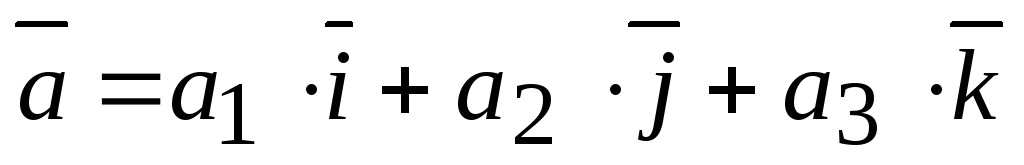 :
:
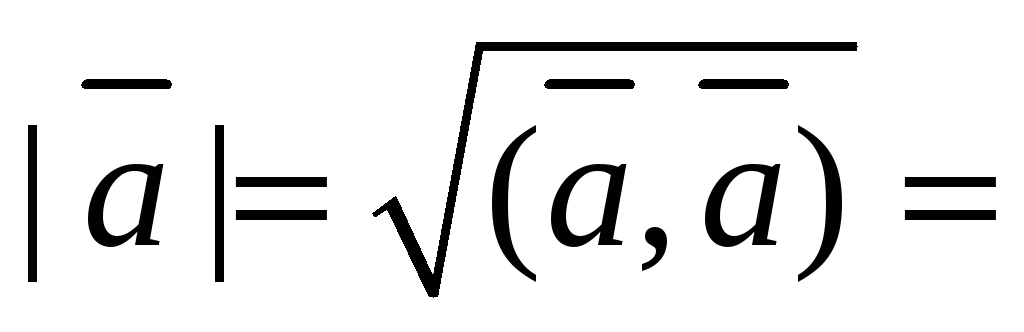
![]()
-
расстояние d между точками
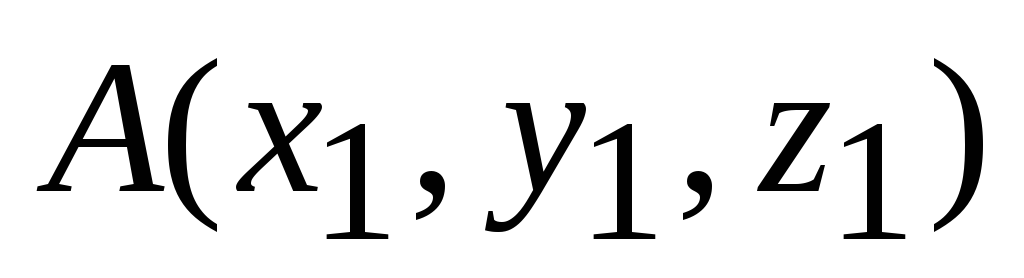 и
и
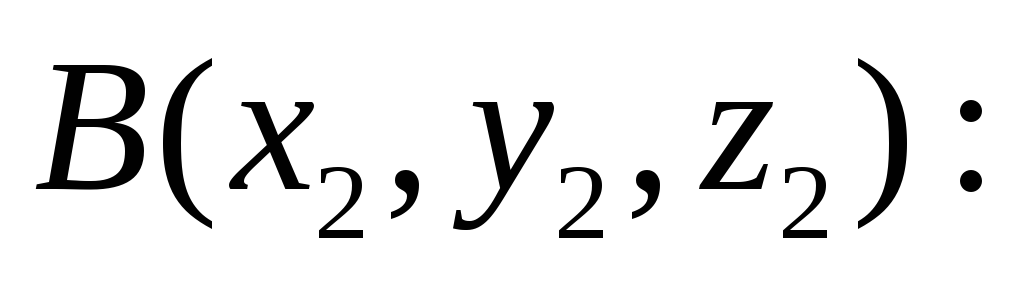
![]()
-
проекцию одного вектора
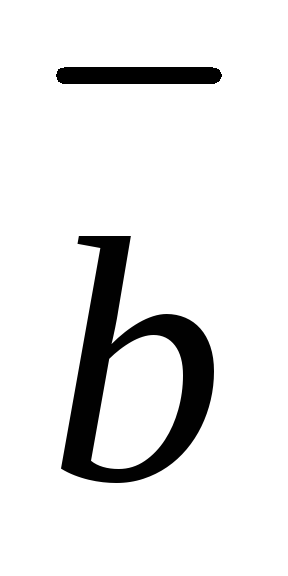 на направление другого вектора
на направление другого вектора
 :
:
![]()
-
косинус угла между векторами:
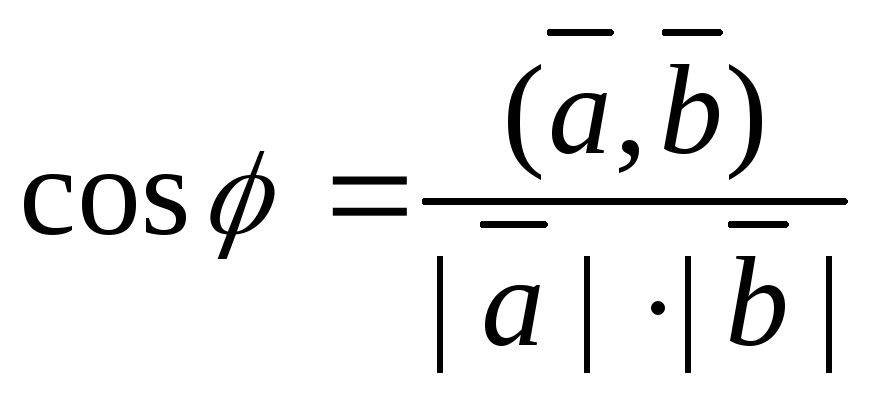 ,
где j
– угол между векторами
,
где j
– угол между векторами
 и
и
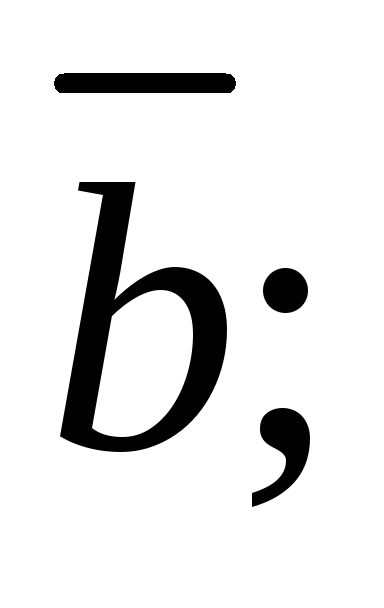
-
координаты орта вектора
 совпадают с его направляющими косинусами:
совпадают с его направляющими косинусами:
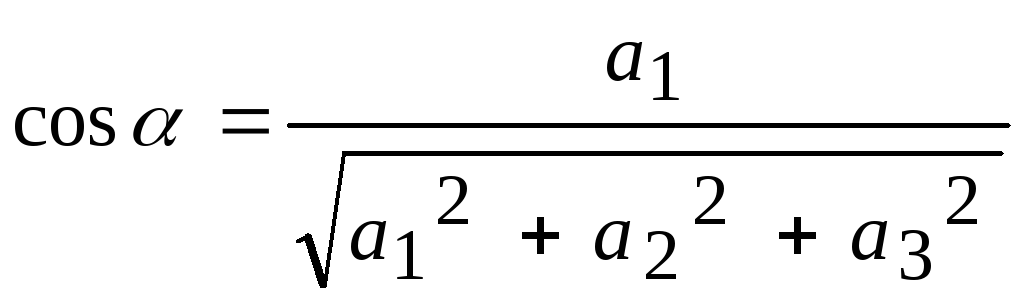 ,
,
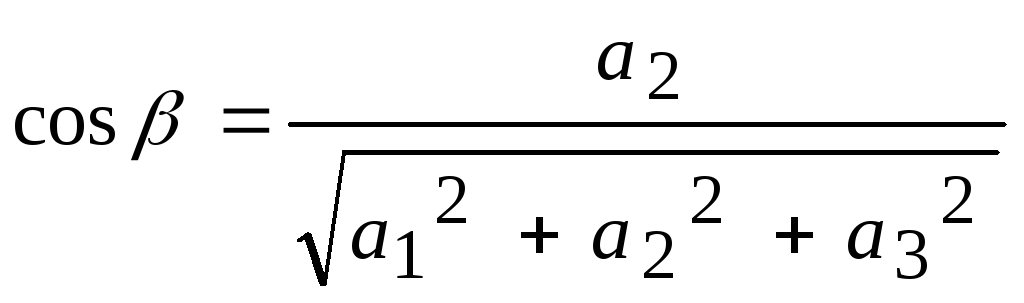 ,
,
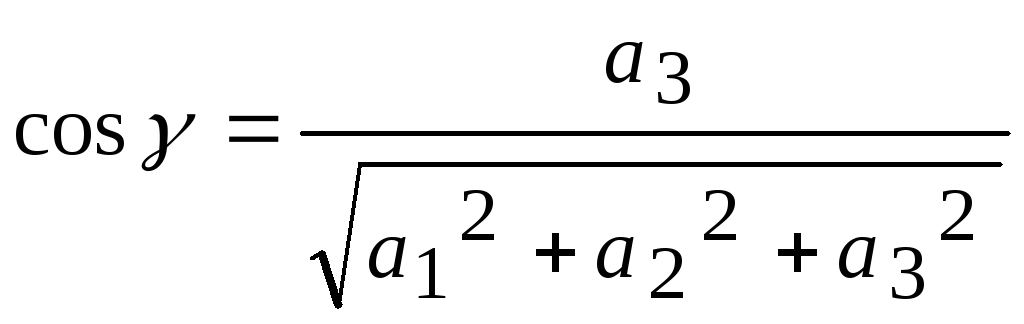 .
.
Пример 4.3.
Найти такое число l,
для которого векторы
![]() и
и
![]() ортогональны.
ортогональны.
Решение. Скалярное
произведение ортогональных векторов
равно нулю, поэтому
![]()
![]() ,
получили линейное алгебра-ическое
уравнение относительно l,
отсюда
,
получили линейное алгебра-ическое
уравнение относительно l,
отсюда
![]() или
или
![]() ,
то есть при
,
то есть при
![]() векторы
векторы
![]() и
и
![]() будут ортогональны. В самом деле, имеем
будут ортогональны. В самом деле, имеем
![]() .
.
Пример 4.4.
Найти углы и длины сторон треугольника
с вершинами
![]()
![]()
![]() .
.
Решение.
Определим
координаты векторов:
![]() ,
,
![]() ,
,
![]() ,
так как угол A
образован векторами
,
так как угол A
образован векторами
![]() и
и
![]() ,
то
,
то
![]() .
.
По таблицам находим
![]() .
.
Аналогично
![]() ,
значит,
,
значит,
![]() – прямой. Поскольку сумма углов
треугольника равна 180°,
то
– прямой. Поскольку сумма углов
треугольника равна 180°,
то
![]() .
Длины сторон – это длины соответст-вующих
векторов, поэтому:
.
Длины сторон – это длины соответст-вующих
векторов, поэтому:
![]() ;
;
![]() ;
;
![]() .
.
Пример
4.5.
Найти скалярное произведение векторов
![]() и
и
![]() ,
если
,
если
![]() ,
,
![]() ,
а
угол между векторами
,
а
угол между векторами
![]() и
и
![]() равен
60°.
равен
60°.
Решение. Выполним последовательные действия:
![]()
![]()
![]() .
.
Векторное и смешанное произведение векторов
Определение.
Векторным
произведением двух неколлинеарных
векторов
![]() и
и
![]() называется третий вектор
называется третий вектор
![]() ,
обозначаемый
,
обозначаемый
![]() или
или
![]() и удовлетворяющий следующим условиям:
и удовлетворяющий следующим условиям:
-
вектор
 ортогонален каждому из векторов
ортогонален каждому из векторов
 и
и
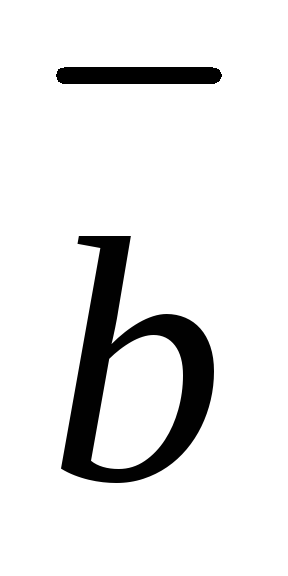 ,
то есть перпендикулярен плоскости, в
которой лежат эти векторы;
,
то есть перпендикулярен плоскости, в
которой лежат эти векторы; -
если векторы
 ,
,
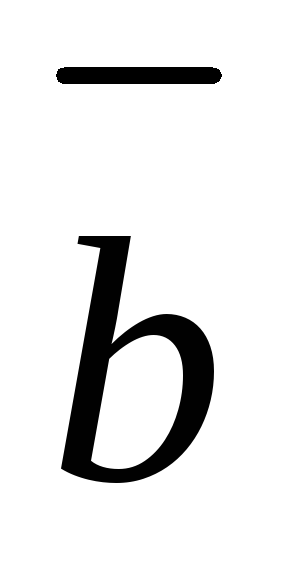 ,
,
 отложены от одной точки O,
то с конца вектора
отложены от одной точки O,
то с конца вектора
 поворот от вектора
поворот от вектора
 к вектору
к вектору
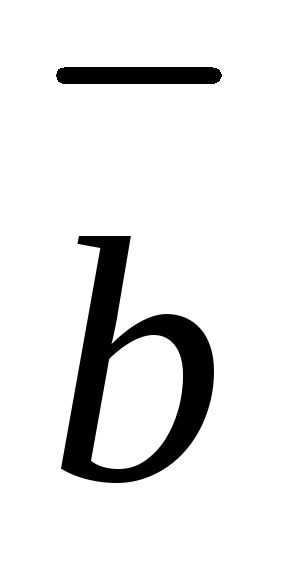 на меньший угол осуществляется против
часовой стрелки (в этом случае тройка
на меньший угол осуществляется против
часовой стрелки (в этом случае тройка
 ,
,
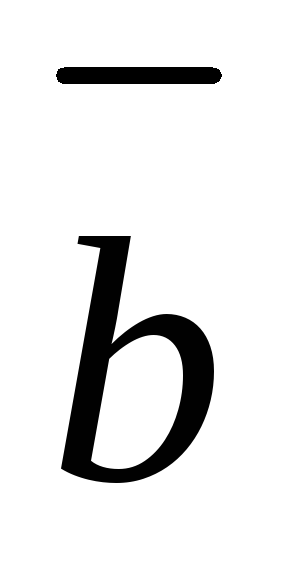 ,
,
 называется правой);
называется правой); -
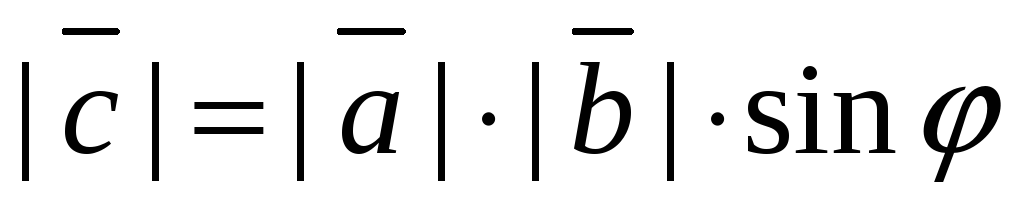 ,
где j
– угол между
векторами
,
где j
– угол между
векторами
 и
и
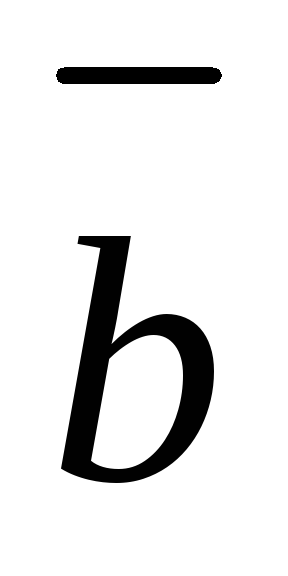 .
.
Если
векторы
![]() и
и
![]() коллинеарны, то полагают
коллинеарны, то полагают
![]() .
.
Свойства векторного произведения
-
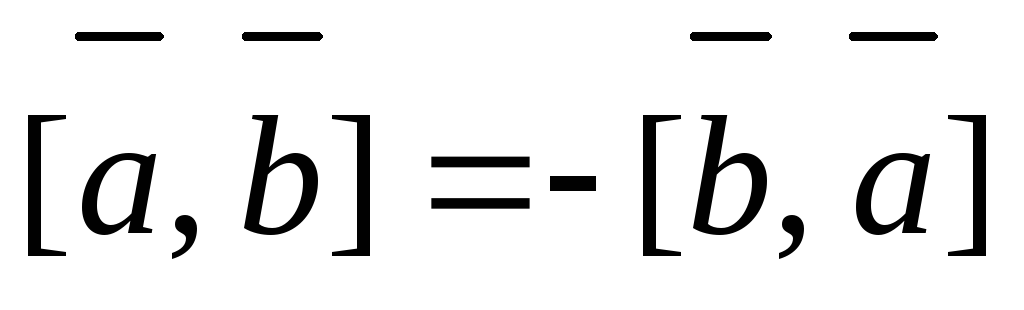 ;
; -
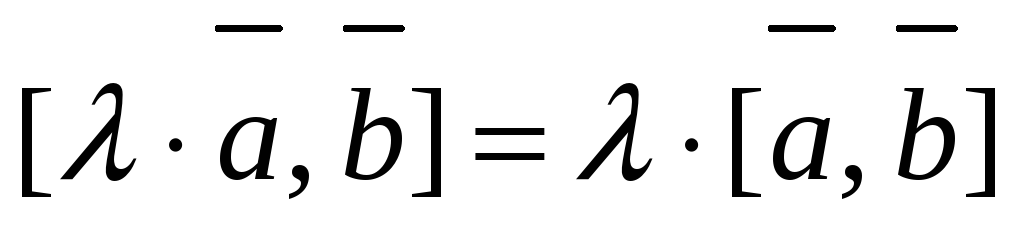 ;
; -
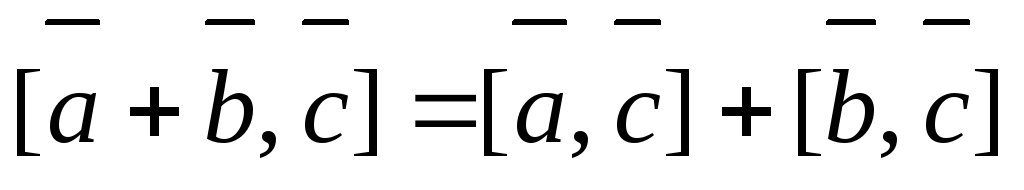 ;
; -
величина модуля векторного произведения
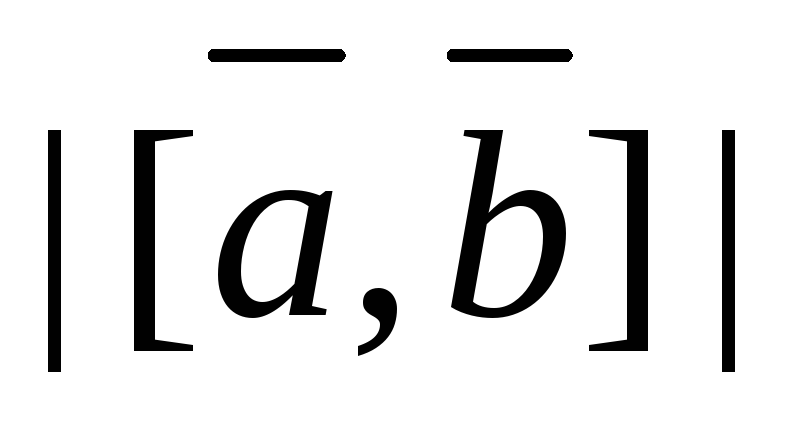 двух неколлинеарных векторов равна
площади параллелограмма, постро-енного
на векторах
двух неколлинеарных векторов равна
площади параллелограмма, постро-енного
на векторах
 и
и
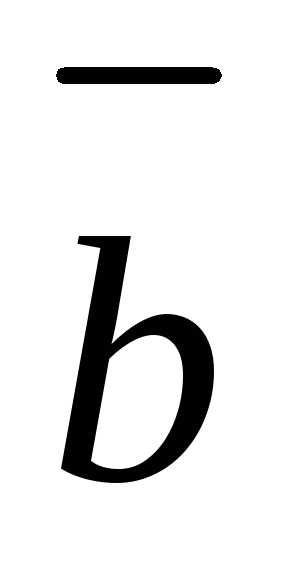 ;
; -
координаты векторного произведения векторов
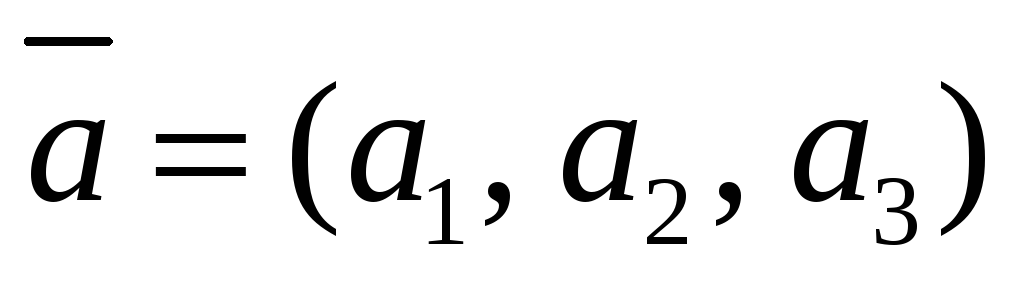 и
и
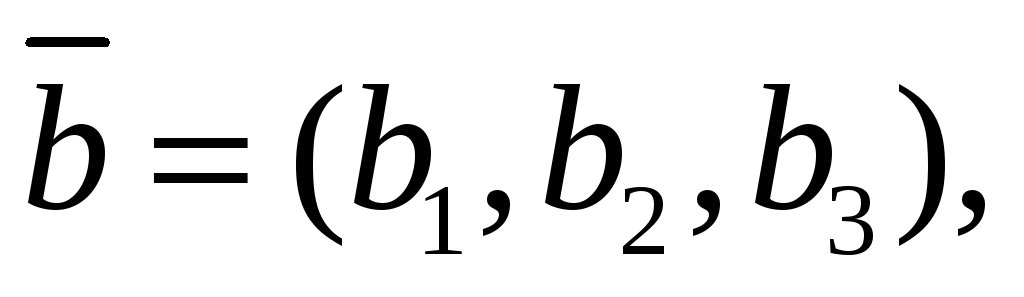 заданных координатами, можно найти
следующим образом:
заданных координатами, можно найти
следующим образом:
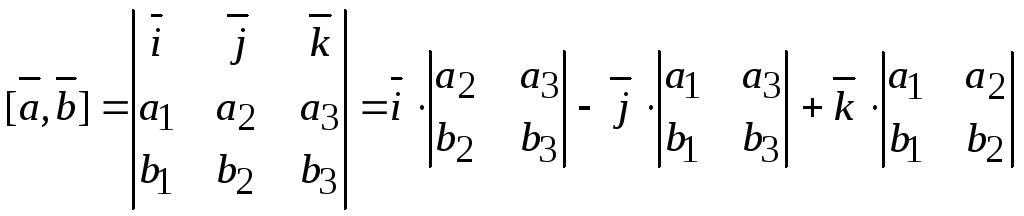 .
.
Определение.
Смешанным произведением трех векторов
![]() ,
,
![]() ,
,
![]() называется скалярное произведение
первого из них и векторного произведения
второго и третьего. Обозначается
смешанное произведение
называется скалярное произведение
первого из них и векторного произведения
второго и третьего. Обозначается
смешанное произведение
![]() или просто
или просто
![]() .
.
Свойства смешанного произведения
-
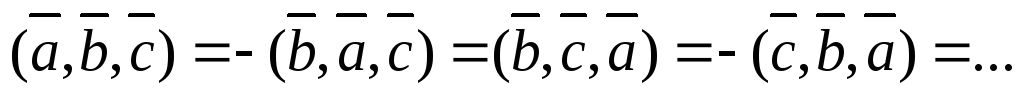 – то есть
пере-становка двух соседних векторов
местами ведет к смене знака смешанного
произведения;
– то есть
пере-становка двух соседних векторов
местами ведет к смене знака смешанного
произведения; -
модуль смешанного произведения
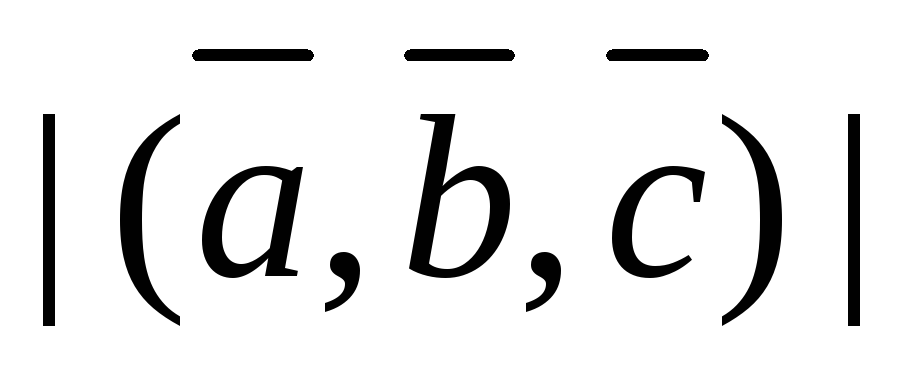 трех неком-планарных векторов равен
объему параллелепипеда, построенного
на век-торах
трех неком-планарных векторов равен
объему параллелепипеда, построенного
на век-торах
 ,
,
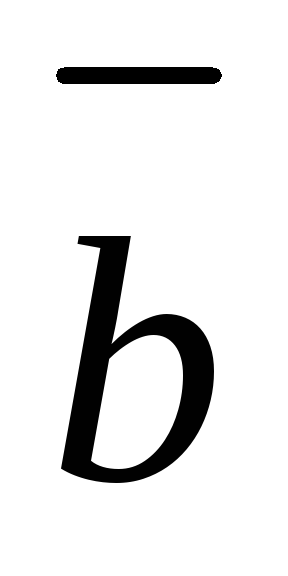 ,
,
 (при этом
(при этом
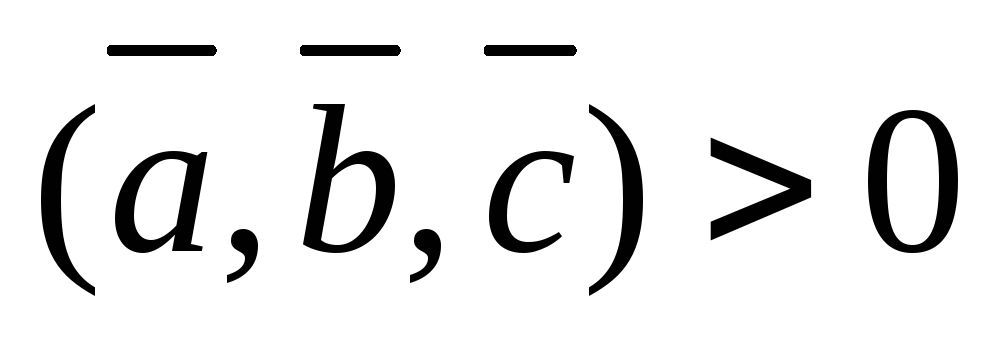 ,
если тройка
,
если тройка
 ,
,
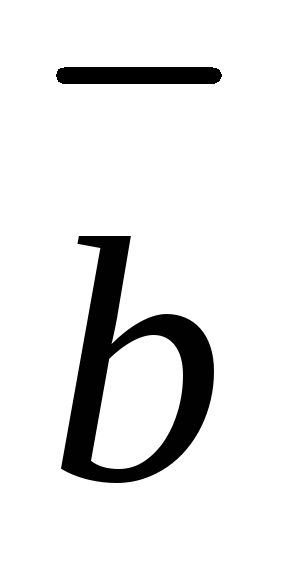 ,
,
 – правая и
– правая и
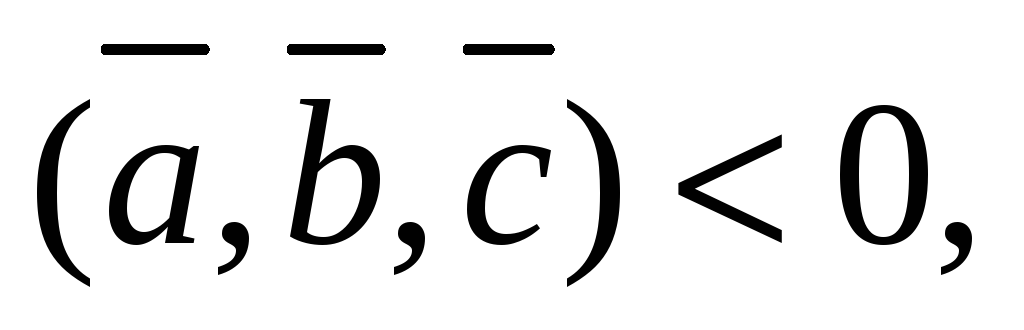 если тройка векторов – левая);
если тройка векторов – левая); -
если векторы
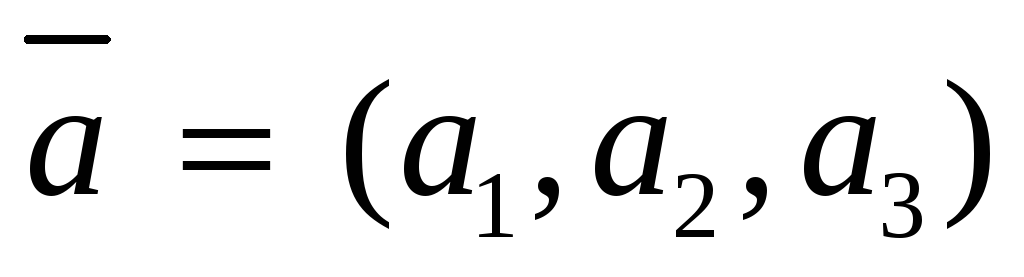 ,
,
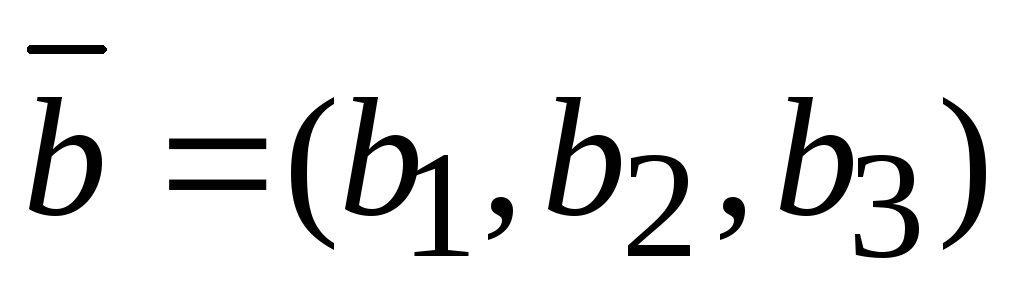 ,
,
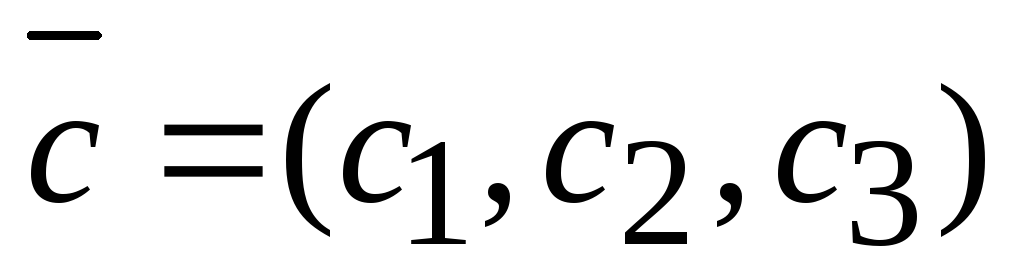 заданы координатами, то
заданы координатами, то
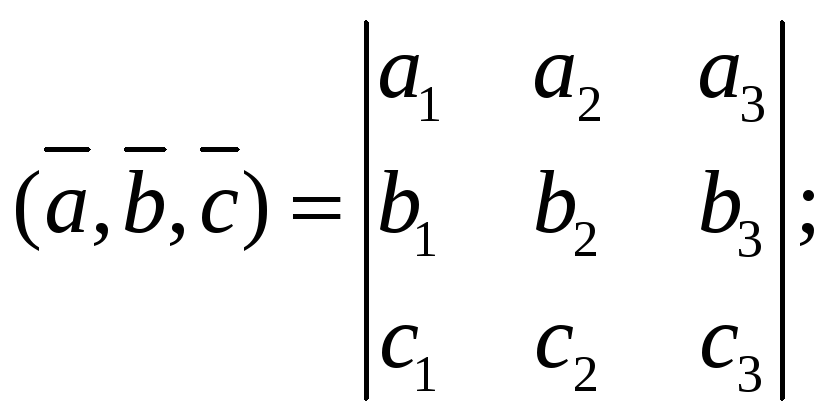
-
три вектора
 ,
,
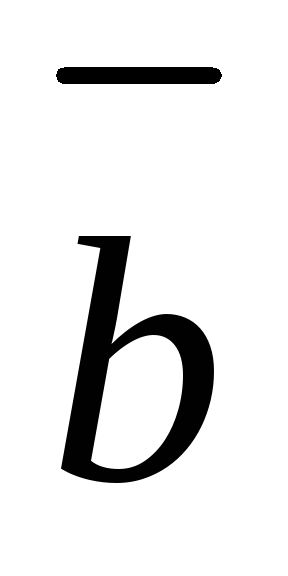 ,
,
 лежат в одной плоскости (компланарны)
тогда и только тогда, когда их смешанное
произведение равно нулю.
лежат в одной плоскости (компланарны)
тогда и только тогда, когда их смешанное
произведение равно нулю.
Пример 4.6.
Найти площадь треугольника АВС
с верши-нами
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Воспользуемся свойством 4 векторного
про-изведения: площадь треугольника
равна половине площади па-раллелограмма,
построенного на векторах
![]() и
и
![]() Вычислим их векторное произведение,
имеем:
Вычислим их векторное произведение,
имеем:
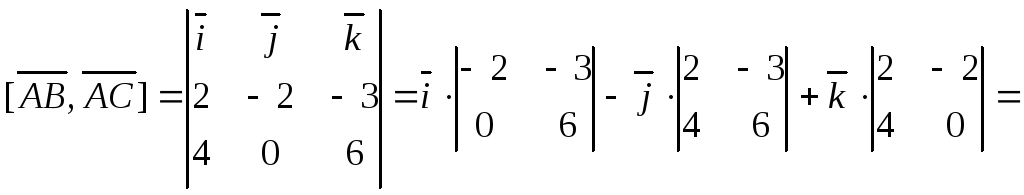
![]()
![]() .
.
Площадь треугольника ABC равна половине величины этого векторного произведения:
![]() кв.
ед.
кв.
ед.
Пример 4.7.
Найти объем тетраэдра, вершинами которого
являются точки
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Решение.
Объем тетраэдра составляет шестую часть
объема парал-лелепипеда, построенного
на векторах
![]() ,
,
![]() и
и
![]() Найдем
смешанное произведение этих векторов:
Найдем
смешанное произведение этих векторов:
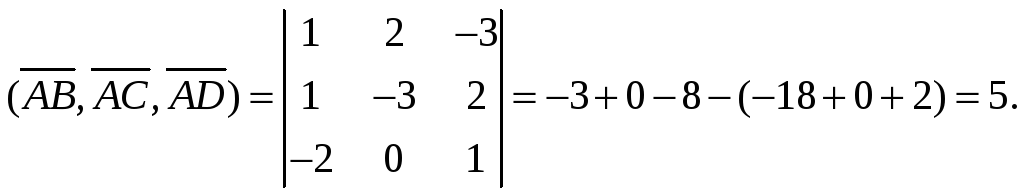
![]()
Таким образом,
объем тетраэдра равен
![]() куб. ед.
куб. ед.
