Базис системы векторов

Определение. Система векторов , , называется линейно зависимой, если существуют такие константы , , не все равные нулю, поэтому имеет место равенство

.

Если из этого равенства с необходимостью следует, что , то система называется линейно независимой.

Определение. Базисом в трехмерном пространстве назы-вается любая упорядоченная система из трех линейно независи-мых векторов пространства.

Теорема 4.1. Векторы , , Î L³ образуют базис тогда и только тогда, когда D ¹ 0, где .

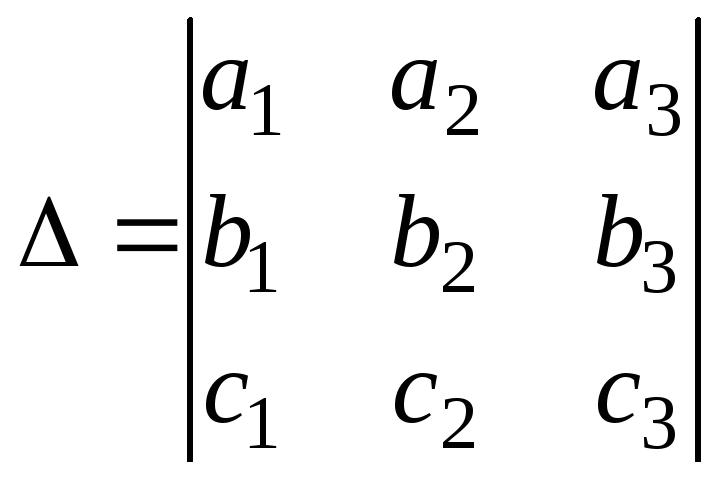Доказательство

1) Необходимость. Пусть векторы образуют базис, тогда по определению эти векторы линейно независимые, а следовательно, равенство

которое эквивалентно однородной системе

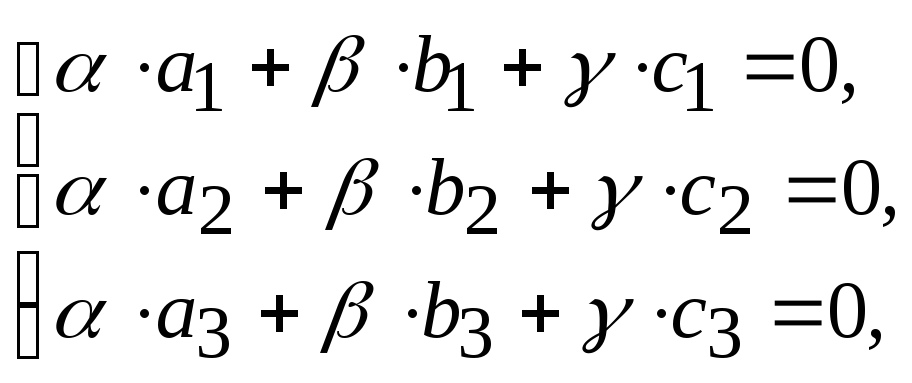
выполняется только в случае . Однородная система линейных алгебраических уравнений имеет единственное нуле-вое решение только в том случае, когда

.

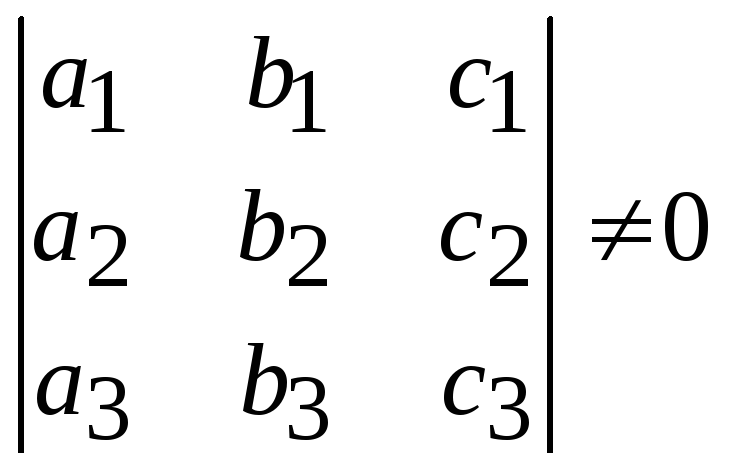По 1-му свойству определителей (С. 13) получаем:

.

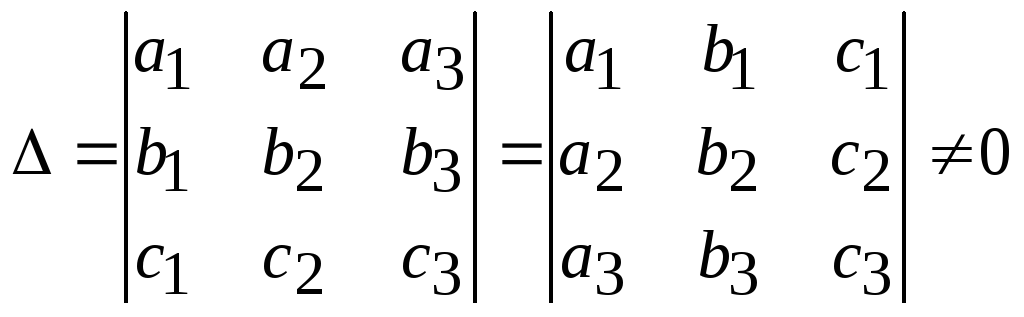Необходимость доказана.

2) Достаточность. Пусть для векторов , пространства L³ выполняется

.

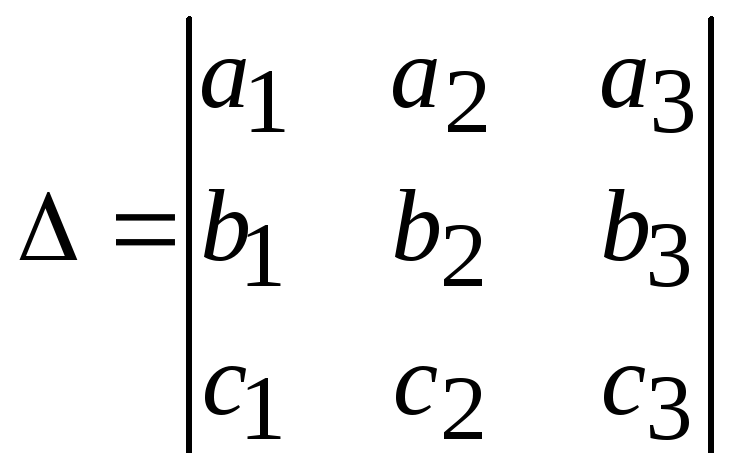Проверим линейную независимость векторов , составим равенство , рассмотрим однород-ную систему уравнений

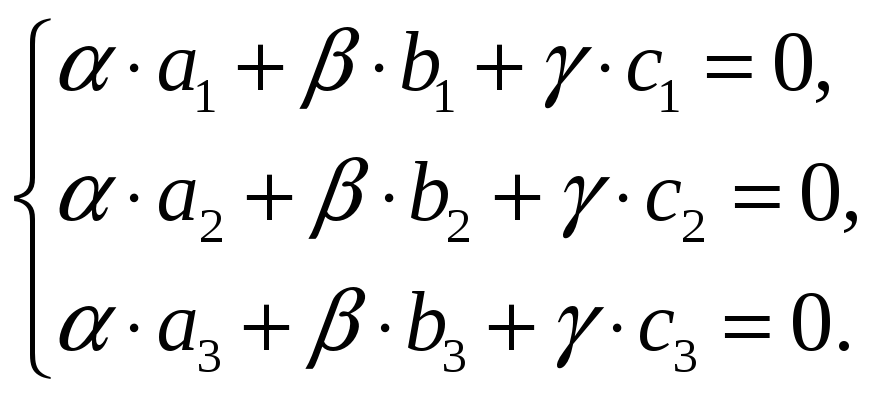
Так как определитель, составленный из коэффициентов при неизвестных системы, не равен нулю, т. е.

,

то эта система имеет единственное нулевое решение, по определению векторы образуют систему линейно независимых векторов, а следовательно, и базис в пространстве L³. Теорема доказана.

Если векторы , , образуют базис, а вектор представляется в виде , тогда числа , , называются координатами вектора в базисе , , , то есть .

Пример 4.2. Даны три вектора , , . Показать, что они образуют базис и найти разложение вектора в этом базисе.

Решение. Покажем, что векторы , , образуют базис. Вычислим определитель, составленный из координат этих векторов:

.

Так как D ¹ 0, то по теореме 4.1 векторы , , образуют базис. Отсюда получаем разложение вектора по базисным векторам , , :

Û .

Чтобы найти координаты , , вектора в новом базисе, необходимо найти решение следующей системы уравнений:

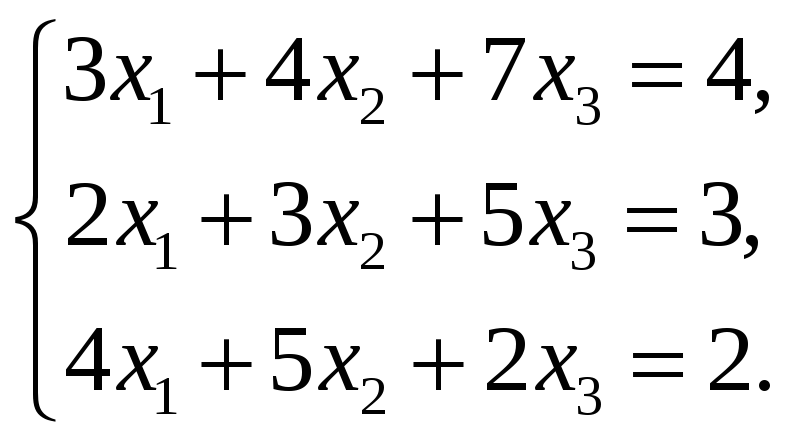
Решим эту систему методом Крамера, имеем:

, ,

, .

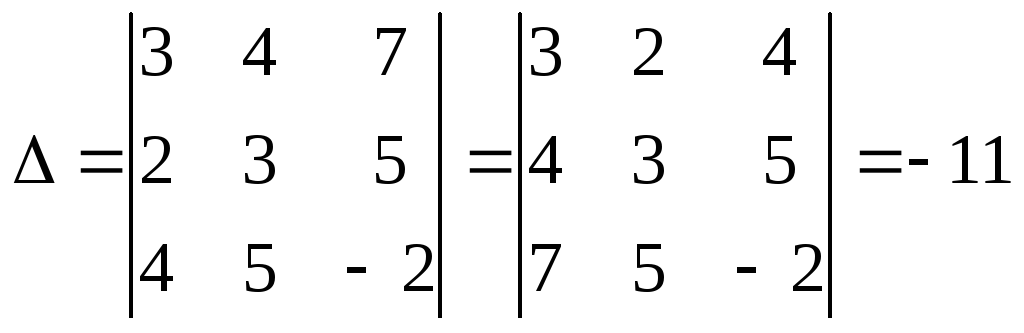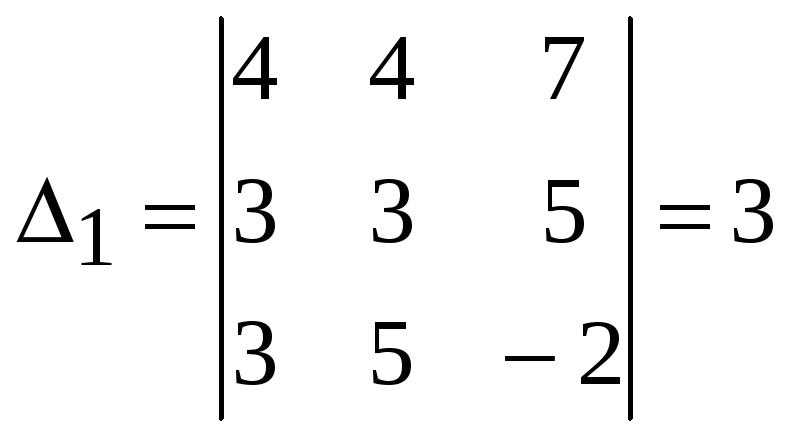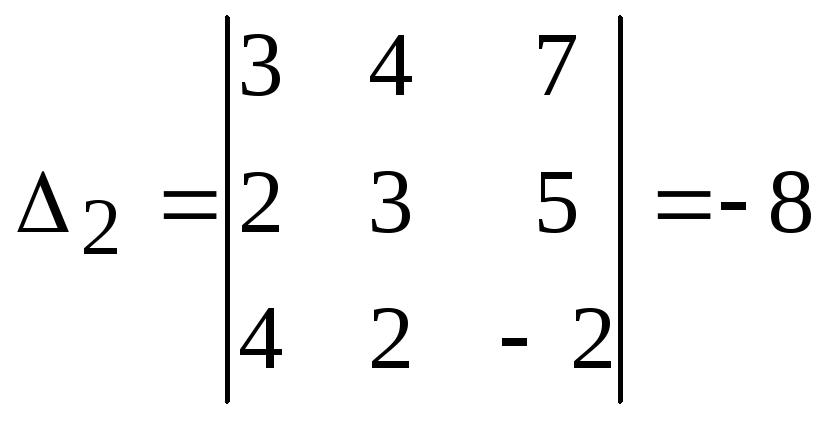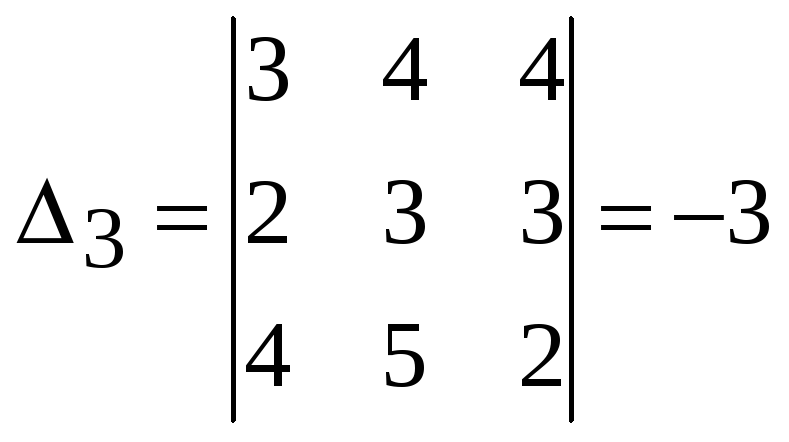Так как D ¹ 0, то система совместна и имеет единственное решение: , , . То есть

.

Определение. Совокупность всех трехмерных векторов с действительными координатами, рассматриваемая с определенными в ней операциями сложения векторов и умножения вектора на число, образует трехмерное векторное пространство.

Скалярное произведение векторов

До сих пор мы изучали понятие линейности и не касались количественных характеристик: угла и длины, что особенно важно для приложений. Для лучшего усвоения дальнейшего материала рассмотрим двумерное линейное пространство над полем действительных чисел с введенной в нем декартовой прямоугольной системой координат.

Пусть , . Тогда длина отрезка, соединяющего концы векторов , , находится по очевидной формуле Для расстояния до от начала введем обозначения Перейдем к уг-лам между векторами. Если j – угол между отрезком, соеди-няющим O с и положительной осью Ox, а – угол между отрезком, соединяющим O с и той же осью, то углом между векторами и будет , тогда

.

Введем обозначение

.

С помощью полученного выражения можно очень простыми формулами выразить углы между векторами их длины.

Определение. Скалярным произведением нену-левых векторов и называется число, равное произве-дению их модулей на косинус угла между ними, то есть

Если хотя бы один из векторов и нулевой, то скалярное произведение равно нулю.

Для обозначения скалярного произведения часто используется запись .

Из определения следует, что скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда векторы ортогональны (угол между ними 90°, а