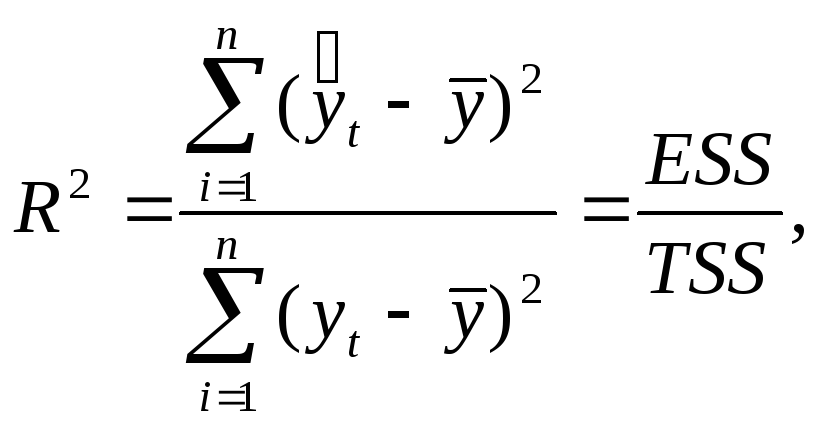Рассмотрим практическую оценку влияния отдельных факторов на зависимую переменную в построенной модели регрессии.

Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако с их помощью непосредственно нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости.

Для устранения таких различий и противоречий для анализа и интерпретации применяются средние частные коэффициенты эластичности Э(j) и -коэффициенты (j), которые рассчитываются соответственно по формулам:

,

,

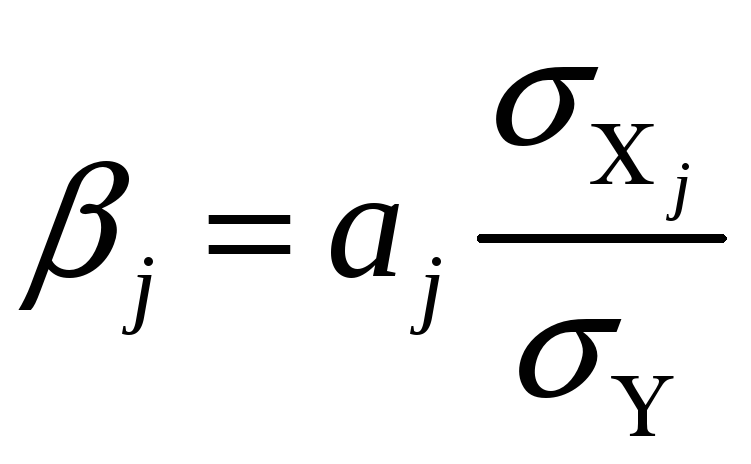где - среднее квадратическое отклонение фактора j.

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении j-го фактора на 1 %. Однако здесь не учитывается степень колеблемости факторов.

Бета-коэффициент характеризует часть величины средне­го квадратического отклонения а _х на которую изменится зависимая переменная Y с изменением соответствующей независимой переменной Х_j на величину своего среднего квадратического отклонения при фиксиро­ванном постоянном уровне значений остальных независимых пере­менных.

Указанные коэффициенты позволяют ранжировать факторы по степени их влияния на зависимую переменную.

Долю влияния фактора в суммарном влиянии всех факторов на результативный признак можно оценить по величине дельта-коэффициентов j

j=r_Yj _j/R²,

где r_Yj - коэффициент парной корреляции между j-ым фактором (j = 1, ..., т) и зависимой переменной.

Разберём вопрос использования многофакторных моделей для анализа и прогнозирования развития экономических систем.

Одна из важнейших целей моделирования заключается в прогнозировании поведения исследуемого объекта. Обычно термин «прогнозирование» используется в тех ситуациях, когда требуется предсказать состояние системы в будущем. Для регрессионных моделей он имеет более широкое значение. Как уже отмечалось, данные могут не иметь временной структуры, но и в этих случаях вполне может возникнуть задача оценки значения зависимой переменной для некоторого набора независимых, объясняющих переменных, которых нет в исходных наблюдениях. Именно в этом смысле - как построение оценки зависимой переменной - и следует понимать прогнозирование в данной науке.

Проблема прогнозирования имеет много различных аспектов. Можно различать точечное и интервальное прогнозирование. В первом случае оценка - это конкретное число, во втором - интервал, в котором истинное значение переменной находится с заданным уровнем доверия. Кроме того, для временных рядов при нахождении прогноза существенно наличие или отсутствие корреляции по време­ни между ошибками.

При использовании построенной модели для прогнозирования делается предположение о сохранении в период прогнозирования существовавших ранее взаимосвязей переменных.

Для прогнозирования зависимой переменной на N шагов вперед необходимо знать прогнозные значения всех входящих в нее факто­ров. Их оценки могут быть получены с использованием МНК или на основе временных экстраполяционных моделей, а также могут быть заданы непосредственно пользователем. Эти оценки должны быть подставлены в модель, и таким образом получены прогнозные оценки.

Важен вопрос о факторах, влияющих на ширину доверительного интервала. Для того чтобы определить область возможных значений результативного показателя при рассчитанных значениях факторов, следует учитывать два возможных источника ошибок: ошибки, обусловленные рассеиванием наблюдений относительно линии регрессии и ошибки, обусловленные математическим аппаратом построения самой линии регрессии. Ошибки первого рода измеряются с помощью характеристик точности, в частности величиной S_e.

Ошибки второго рода обусловлены фиксацией численного значения коэффициентов регрессии, в то время как они в действительности являются случайными, нормально распределенными.

Для линейной модели доверительный интервал рассчитывается следующим образом. Оценивается величина отклонения U от линии регрессии:

U(l) = S_et_кр, (4)

где V_np⁼X_пр^T(X^T X)^-1 Х_пр,

X_пр =(X_1(n+1),X_21(n+1)),...,X_m1(n+1)).

Для модели парной регрессии формула (4) принимает вид:

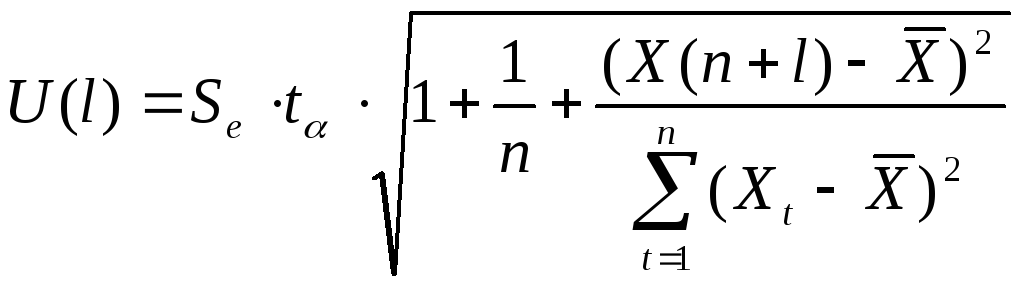. (5)

Коэффициент t_ является табличным значением t-статистики Стьюдента при заданном уровне значимости  и числа наблюдений n, l-период прогнозирования.

Если исследователь задает вероятность попадания прогнозируемой величины внутрь доверительного интервала, равную 0,7 то t_=1,05,

если вероятность составляет 0,95, то t_=l,96, a при 0,99 t_=2,65.

Как видно из формулы (5), величина U прямо пропорционально зависит от точности модели S_e, коэффициенту доверительной вероятности t_, степени удаления прогнозной оценки фактора X от среднего значения и обратно пропорциональна объему наблюдений.

В результате получается следующий интервал прогноза для шага прогнозирования l:

• верхняя граница прогноза равна

Y(n + l) + U/(l),

• нижняя граница прогноза равна

Y(n + l) - U(l).

Если построенная регрессионная модель адекватна и прогнозные оценки факторов достаточно надежны, то с заданным уровнем значимости можно утверждать, что при сохранении сложившихся закономерностей развития прогнозируемая величина попадет в интервал, образованный нижней и верхней границами.

1.2. ПРАКТИЧЕСКИЕ ПРИМЕРЫ ПОСТРОЕНИЯ МОДЕЛЕЙ ВЗАИМОСВЯЗИ С ИСПОЛЬЗОВАНИЕМ ПАКЕТА АНАЛИЗА

MICROSOFT EXCEL

Используемый в данном разделе Пакет анализа – это, как известно, надстройка программы Excel, которая предоставляет широкие возможности для проведения статистического анализа в направлении исследования регрессионных и корреляционных процессов.

Для установки средств Пакет анализа в стандартной конфигурации программы Excel нет средства Пакет анализа. Это средство надо установить в качестве надстройки Excel. Для этого в зависимости от версии используемого программного средства необходимо выполнить действия, описываемые ниже.

При использовании версий ниже W2003 необходимо:

1. Выбрать команду Сервис => Надстройки.

2. В диалоговом окне Надстройки (рис. 2) установить флажок Пакет анализа.

3. Щелкнуть по кнопке ОК.

В результате выполненных действий в нижней части меню Сервис появится новая команда Анализ данных. Эта команда предоставляет доступ к средствам анализа, которые есть в Excel.

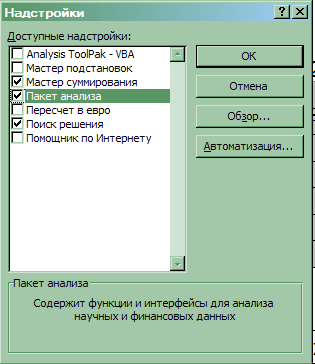
Рис. 2. Диалоговое окно Надстройки

При использовании версии Win2007, в параметрах Excel и диалоговом окне Надстройки также необходимо активизировать Пакет анализа

В результате выполненных действий появится новая команда Анализ данных. Эта команда предоставляет доступ к нужным средствам анализа, имеющимся в Excel.

Пример 1. Простейшее вычисление коэффициента корреляции в программе Microsoft Excel возможно с помощью функции КОРРЕЛ при задании характеристик следующим образом:

КОРРЕЛ (массив 1; массив 2),

где массив 1=диапазон данных для первой переменной,

массив 2=диапазон данных для второй переменной.

Так, в табл. 3 представлены выборочные данные об успеваемости шести студентов отобранных случайным образом.

Таблица 3

Экзаменационная оценка	Количество часов, затраченное на самоподготовку в учебе
3	86
5	95
4	92
4	83
2	78
3	82

На рис. 3 показана функция КОРРЕЛ, используемая при вычислении коэффициента корреляции для данного примера с экзаменационными оценками.

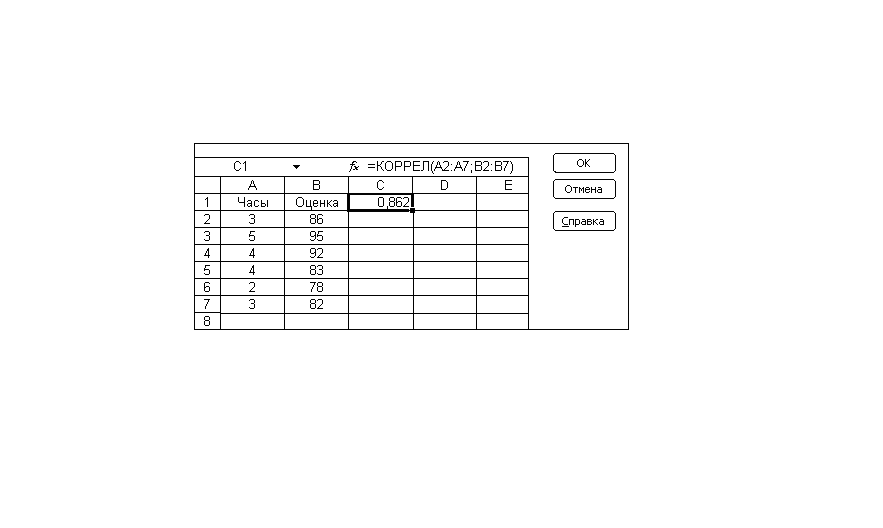
Рис. 3. Функция КОРРЕЛ на примере с экзаменационными оценками

Ячейка С1 содержит формулу = КОРРЕЛ(А2:А7; В2:В7) с результатом 0,862. Полученное значение фактического коэффициента корреляции r свидетельствует о наличии прямой тесной связи между успеваемостью и затратами времени на самоподготовку.

Пример 2. Рассмотрим возможности использования Excel для построения простейшей модели линейной регрессии.

Определим наличие линейной связи между временем и количеством реализованной машиностроительной продукции по видам из всего ассортиментного ряда на складе готовой продукции, используя возможности Excel.

Таблица 4

Реализация продукции по месяцам

Месяц	1	2	3	4	5	6	7	8	9	10
Число видов реализованной продукции	8	6	10	6	10	13	9	11	15	17

Введём данные на рабочее поле Excel в столбцы А и В чистого листа.

1. Активизируем меню Tools (Сервис) и надстройку Data Analysis (Анализ данных).

2. В окне Data Analysis (Анализ данных) выберем опцию Regression (Регрессия), как показано на рис. 4, и щелкнем ОК.

Рис. 4. Выбор опции линейной регрессии в Excel

3. Установим необходимые параметры регрессии в окне Regression (Регрессия), как показано на рис. 5. Щелкнем ОК и получим результаты, показанные на рис.5.

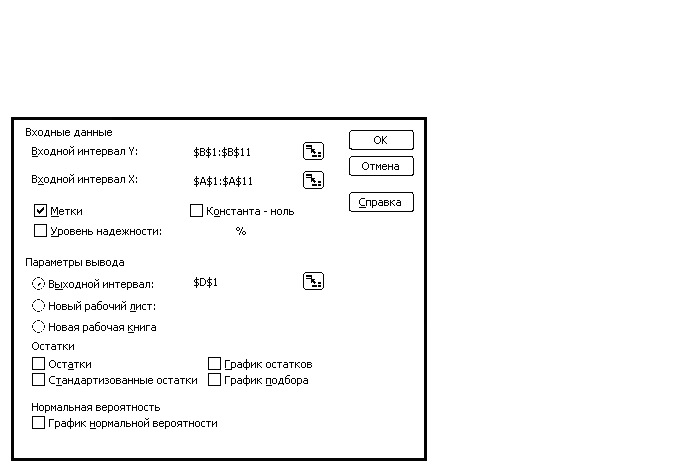
Рис. 5. Диалоговое окно Regression (Регрессия)

.

Рис. 6. Результаты регрессионного анализа в Excel

Поскольку уровень р-значимости для независимой переменной «Месяц» равен 0,00414, а это меньше α=0,01, следует отклонить основную гипотезу о независимости распределения во времени переменных и сделать вывод о существовании линейной связи между ними.

Пример 3. Оценим эффективность применения различных технологий в процессе производства и выполним однофакторный дисперсионный анализ в Excel по данным табл. 5.

Таблица 5

Выработка по цехам	Технология 1	Технология 2	Технология 3
1	10,0	11,6	8,1
2	8,5	12,0	9,0
3	8,4	9,2	10,7
4	10,5	10,3	9,1
5	9,0	10,3	9,1
6	8,1	12,5	9,5
Среднее значение	9,12	10,92	9,48
Дисперсия	1,01	1,7	0,96

1. На чистом рабочем листе, в столбцы А, В и С введём данные из табл.5.

2. Откроем меню Tools (Сервис) и активизируем Data Analysis (Анализ данных).

3. В окне Data Analysis (Анализ данных) выберем опцию Anova: Single Factor (Однофакторный дисперсионный анализ), как показано на рис. 7, и щелкнем ОК.

Рис. 7. Выбор опции однофакторного дисперсионного

анализа в Excel

4. Укажем требуемые значения для проведения процедуры анализа в появившемся окне однофакторного дисперсионного анализа (рис. 8). Щелкнем ОК.

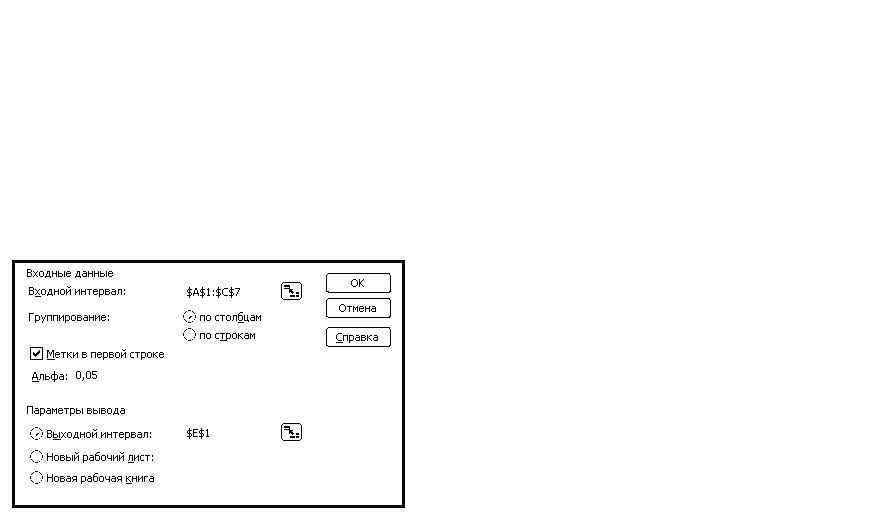
Рис. 8. Диалоговое окно Anova: Single Factor

(Однофакторный дисперсионный анализ)

5. На рис. 9 показаны результаты дисперсионного анализа.

Технология 1

Технология 2

Технология 3

Рис. 9. Результаты дисперсионного анализа

Здесь применялся полностью рандомизированный однофакторный анализ, подразумевающий независимый случайный отбор наблюдений для каждого уровня фактора.

Вариация внутри групп равна 16,45, а вариация между группами 13,01. Если вариация между выборками значительно превышает вариацию внутри выборки, вероятнее всего, что основная гипотеза, состоящая в одинаковом влиянии технологий на результат, будет отклонена.

Для проверки гипотезы о существенности связи воспользуемся значением F- критерия Фишера, которое сравнивается с критическим значением этого параметра. Вычисленное значение F- критерия превышает его критическое, что свидетельствует о неодинаковости средних по совокупности.

Уровень значимости равен 0,0126, а это значит, что следует отклонить Н_о, поскольку уровень р-значимости ≤ α (α=0,05).

Финальное заключение состоит в том, что одна из технологий в большей степени увеличивает производительность труда и даёт лучшие результаты, чем остальные.

Несмотря на то, что основная гипотеза отклонена и пришли к заключению, что средние по генеральной совокупности неодинаковы, ANOVA-анализ не позволяет сравнивать средние между собой, то есть нельзя доказать , что технология 2 лучше технологии 1 и хуже технологии 3. Для этого нужна ещё одна проверка.

Пример 4. Рассмотрим использование функции FРАСПОБР программы EXCEL для установления роли систематической и случайной вариаций в общей вариации и, следовательно, установления роли изучаемого факторного признака в изменении результативного.

Сгенерируем критические F-критерии при помощи функции FРАСПОБР со следующими характеристиками:

FРАСПОБР (вероятность; степени свободы 1; степени свободы 2), где:

• вероятность=уровень значимости;

• степени свободы 1=v₁=k-1;

• степени свободы 2=v₂=N-k.

На рис. 10 показано полученное значение функции FРАСПОБР при определении критического значения F-критерия при α=0,05, v₁=3-1=2 и v₂=18-3=15 для данных предыдущего примера.

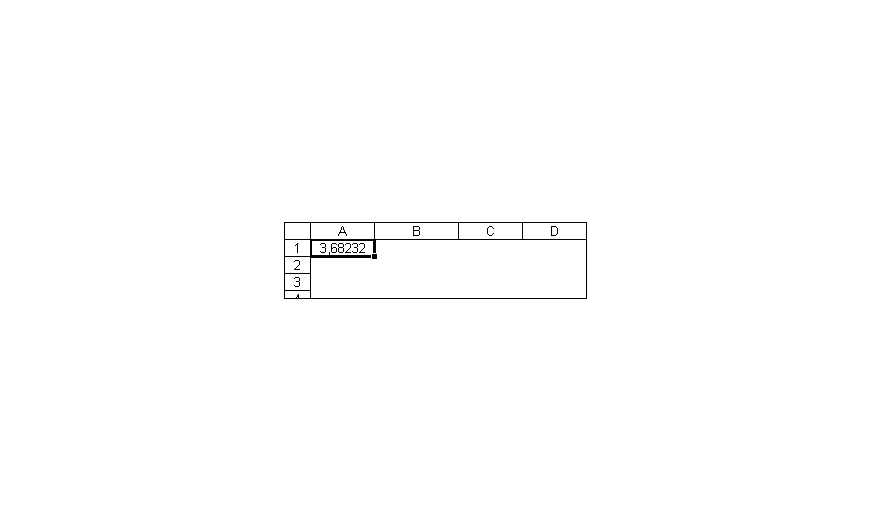
Рис. 10. Функция FРАСПОБР

Ячейка А1 содержит формулу = FРАСПОБР (0,05; 2; 15) с результатом 3,682. Эта вероятность получена в предыдущей таблице. Далее можно определить степень влияния каждой технологии на производительность с помощью проверки Шеффе.

Пример 5. Построим регрессионную модель, выявляющую связь между объемом реализации продукции одного вида от ряда факторных признаков ( временных и ценовых) предприятия.

Объем реализации - это зависимая переменная или результативный признак, обозначенный как Y. В качестве независимых, факторных переменных выбраны:

Х₁ - время,

Х₂ - расходы на материал,

Х₃ - цена изделия,

Х₄ - средняя цена по отрасли,

X₅ - индекс расходов.

Собранные статистические данные по всем факторным признакам приведены в табл. 6.

В рассматриваемом примере число наблюдений составляло n = 16, число факторных признаков т = 5.

Таблица 6

Зависимость между объемом реализации продукции одного вида предприятия и различными факторными признаками

Y	X1	Х2	Х3	Х4	Х5
126	1	4	15	17	100
137	2	4,8	14,8	17,3	98,4
148	3	3,8	15,2	16,8	101,2
191	4	8,7	15,5	16,2	103,5
274	5	8,2	15,5	16	104,1
370	6	9,7	16	18	107
432	7	14,7	18,1	20,2	107,4
445	8	18,7	13	15,8	108,5
367	9	19,8	15,8	18,2	108,3
367	10	10,6	16,9	16,8	109,2
321	11	8,6	16,3	17	110,1
307	12	6,5	16,1	18,3	110,7
331	13	12,6	15,4	16,4	110,3
345	14	6,5	15,7	16,2	111,8
364	15	5,8	16	17,7	112,3
384	16	5,7	15,1	16,2	112,9

Для установления связи будем использовать инструмент Корреляция.

Для проведения корреляционного анализа в данном случае необходимо выполнить следующие действия:

1. Расположить данные в смежных диапазонах ячеек.

2. Выбрать команду Сервис => Анализ данных (рис. 11). Появится диалоговое окно Анализ данных (рис. 12)

Рис.11. Выбор команды Анализ данных

3. В диалоговом окне Анализ данных выбрать инструмент Корреляция (рис.12), щелкнуть по кнопке ОК. Появится диалоговое окно Корреляция (рис.13).

Рис.12. Выбор команды Анализ данных

4. В диалоговом окне Корреляция в поле «Входной интервал» ввести диапазон ячеек, в которых содержатся исходные данные. Если выделены заголовки столбцов, то установить флажок «Метки в первой строке» (рис.13).

5. Выбрать параметры вывода. Для данного примера - установить переключатель «Новый рабочий лист».

6. Щелкнуть по кнопке ОК.

Рис.13. Диалоговое окно Корреляция

На новом рабочем листе получим результаты вычислений в виде таблицы значений коэффициентов парной корреляции (рис.14).

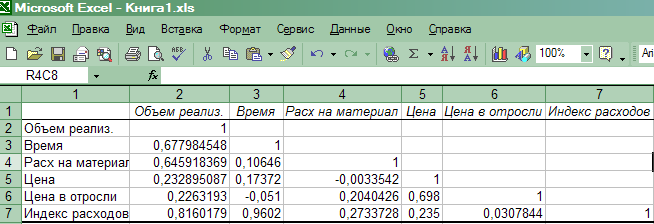
Рис. 14. Результаты корреляционного анализа

Выберем вид модели.

Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т.е. объем реализации, имеет тесную связь:

- с индексом расходов r_yX5 =0,816,

• расходами на материал r_yX2 = 0,646,

• временем r_yX1 = 0,678.

Однако факторы Х₁ и Х₅ тесно связаны между собой : r_X1X5=0,96, что свидетельствует о наличии коллинеарости. Из этих двух пере­менных оставим в модели Х₅ - индекс расходов. Пе­ременные X₁ (время), X₃ (цена изделия) и Х₄ (цена отрасли) также исключаем из модели, т.к. связь их с результативным признаком Y (объемом реализации) невысокая.

После исключения незначимых факторов имеем п=16,k = 2 и модель приобретает вид

= а_о+а₁Х₂+а₂Х₅.

Оценим параметры модели.

На основе метода наименьших квадратов проведем оценку параметров регрессии по формуле (3). При этом используем данные, приведенные в табл.7.

Таблица 7

Y	Х0	X2	X5
Объем реал.		Реклама	Инд. п.расходов
126	1	4	100
137	1	4,8	98,4
148	1	3,8	101,2
191	1	8,7	103,5
274	1	8,2	104,1
370	1	9,7	107
432	1	14,7	107,4
445	1	18,7	108,5
367	1	19,8	108,3
367	1	10,6	109,2
321	1	8,6	110,1
307	1	6,5	110,7
331	1	12,6	110,3
345	1	6,5	111,8
364	1	5,8	112,3
384	1	5,7	112,9

Непосредственное вычисление (вычисление «вручную») вектора оценок параметров регрессии а согласно формуле (3) весьма громоздко, т.к. матрица независимых переменных X имеет довольно вы­сокую размерность (16 х 3), матрица Y- размерности (16 х 1).

В табл. 8 приведены размерности матриц - результатов промежуточных действий.

Таблица 8

XT	(3 х 16)
ХTХ	(3x3)
(XTX)-1	(3x3)
(ХTХ)-1ХT	(3 х 16)
(ХTX)-1ХTY	(3x1)

Задача существенно упрощается при использовании средств Excel. Операции, предписанные формулой (3), целесообразно проводить с помощью следующих встроенных в Excel функций:

•МУМНОЖ - умножение матриц,

•ТРАНСП - транспонирование матриц,

•МОБР - вычисление обратной матрицы.

Для вычисления вектора оценок параметров регрессии а в Excel необходимо выполнить следующие действия:

1. Ввести данные (табл. 6).

2. Выделить диапазон ячеек для записи вектора а, соответствующий его размерности (3x1) (рис. 15).

3. Используя встроенные в Excel функции, ввести формулу (3), определяющую вектор а.

4. Нажать одновременно клавиши CTRL + SHIFT + ENTER. Появится результат (рис. 16).

Таким образом, имеем

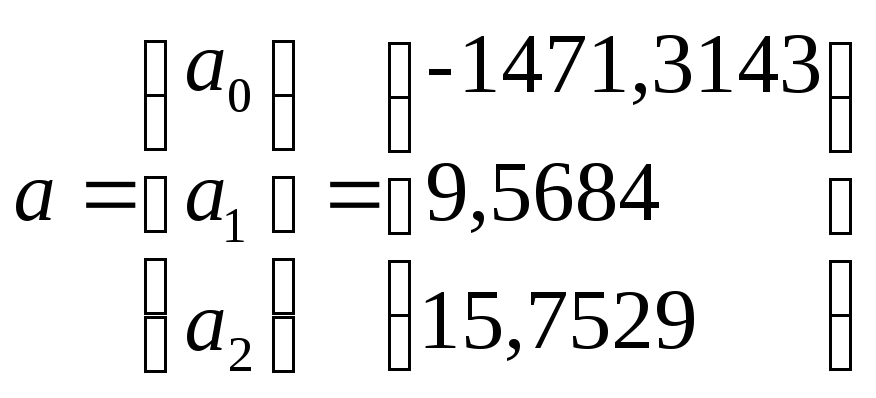
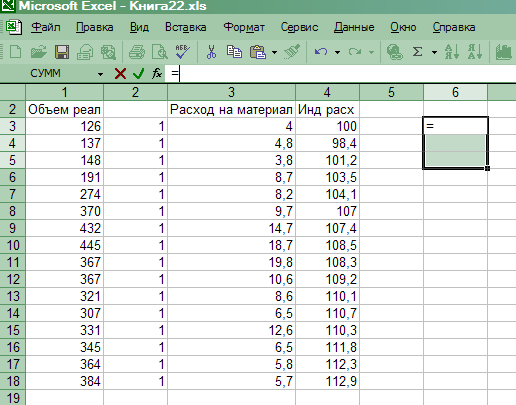
Рис. 15. Выделение диапазона ячеек (3 х 1) для записи вектора оценок параметров регрессии а

Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в виде:

= -1471,3143 + 9,5684 Х₂+15,7529 Х₅.

Расчетные значения Y определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого момента времени t.

Применение инструмента Регрессия в данном случае производится следующим образом.

Для проведения регрессионного анализа с помощью Excel вы­полните следующие действия:

1. Выбрать команду Сервис => Анализ данных.

2. В диалоговом окне Анализ данных выбрать инструмент Регрессия. Щелкните по кнопке ОК.

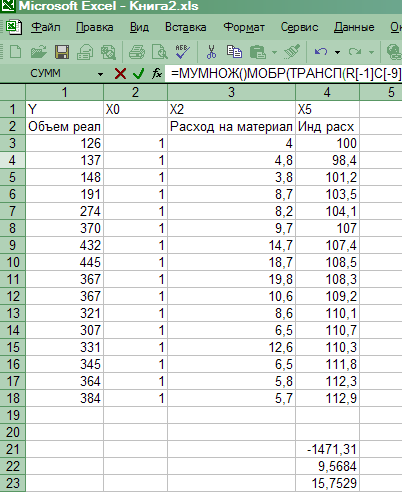
Рис. 16. Результат вычислений - вектор оценок параметров регрессии

3. В диалоговом окне Регрессия в поле «Входной интервал F» ввести адрес диапазона ячеек, который представляет зависимую переменную Y.

4. В поле «Входной интервал X» ввести адреса одного или нескольких диапазонов, которые содержат значения независимых переменных (в рассматриваемом примере - переменные Х₂, Х₅). Если выделены заголовки столбцов, то установить флажок «Метки в первой строке».

5. Выбрать параметры вывода. В данном примере – установить переключатель «Новая рабочая книга».

6. В поле «Остатки» поставить необходимые флажки.

7. Щелкнуть по кнопке ОК.

Результаты представлены на рис. 17 и в таблице на рис.18.

Обозначения в регрессионной статистике
Наименования в отчете Excel	Принятые наименования	Формула
Множественный R	Коэффициент мно­жественной корреляции, индекс корреляции
R - квадрат	Коэффициент детерминации, R2
Нормированный R2	Скорректированный R2
Стандартная ошибка	Стандартная ошибка оценки
Наблюдения	Количество наблю­дений, п	n

Рис.17. «Регрессионная статистика»,

пояснения к таблице на рис.18

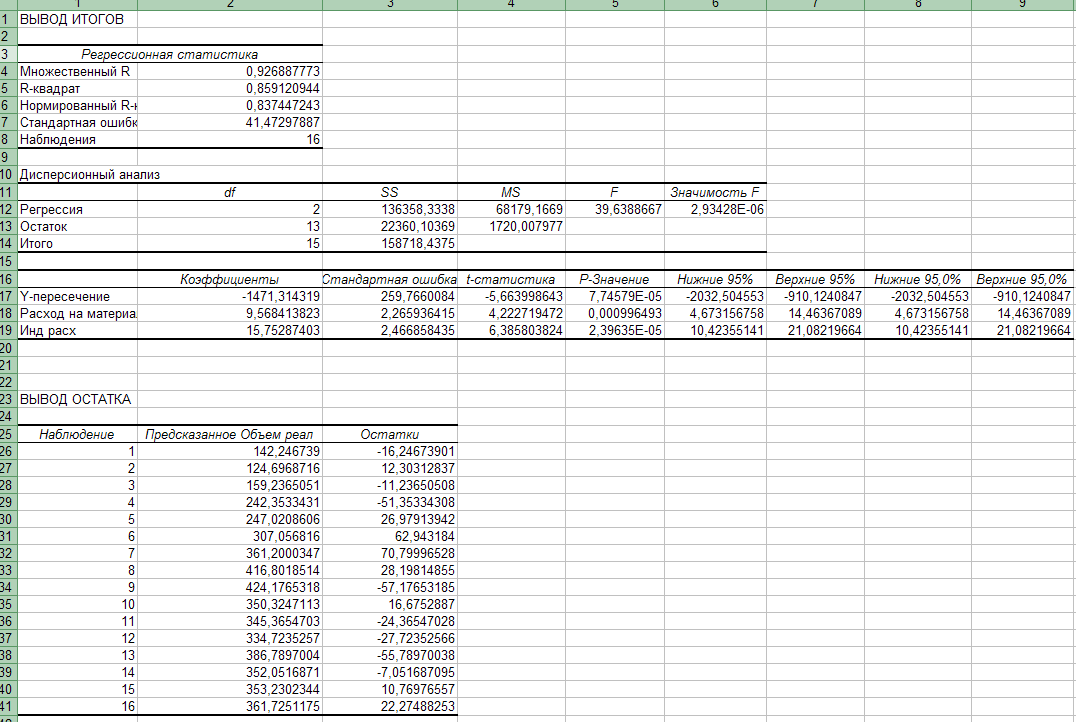
Рис. 18. Результаты регрессионного анализа, проведенного

с помощью Excel

	Df - число степеней свободы	SS -сумма квадратов	MS	F-критерий Фишера
Регрессия	k
Остаток	n-k-1
Итого	n-1

Рис. 19. Пояснения к таблице «Дисперсионный анализ» на рис. 18

Во втором столбце таблицы дисперсионного анализа (рис. 18) содержатся коэффициенты уравнения регрессии а₀, а₁ а₂, в третьем столбце содержатся стандартные ошибки коэффициентов уравнения регрессии, в четвертом - F-статистика, используемая для проверки значимости коэффициентов уравнения регрессии.

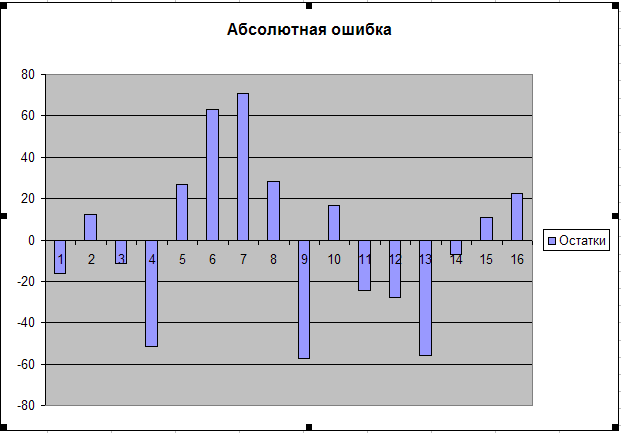
Рис.20. График остатков

Проведём оценку качества модели.

В таблице «Вывод остатка» (рис. 18) приведены вычисленные по модели значения и значения остаточной компоненты е.

Исследование на наличие автокорреляции остатков проведен с помощью d-критерия Дарбина - Уотсона. Для определения величины d-критерия воспользуемся расчетной табл. 9.

Имеем .

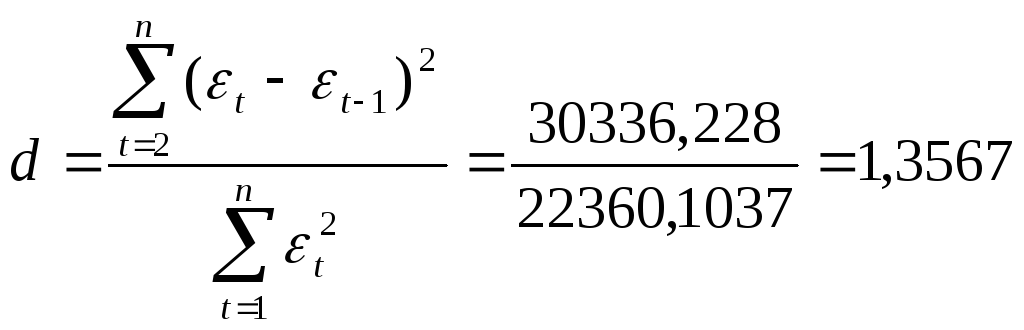В качестве критических табличных уровней при n= 16, двух объясняющих факторах при уровне значимости = 0,05 возьмем величины вd_L = 0,98 и d_U=1,54 (приложения А и Б). Расчетное значение d = 1,3567 попало в интервал от d_L= 0,98 до d_U =1,54 (рис.21)

Таблица 9

Набл.	Y	Предск.Y					(Y-Yср)2
1	126	142,2467	-16,2467	263,9565			32693,1602
2	137	124,6969	12,3031	151,3670	815,0949	-199,8857	28836,2852
3	148	159,2365	-11,2365	126,2590	554,1143	-138,2442	25221,4102
4	191	242,3533	-51,3533	2637,1658	1609,3607	577,0321	13412,5352
5	274	247,0209	26,9791	727,8740	6135,9778	-1385,469	1076,6602
6	370	307,0568	62,9432	3961,8444	1293,4125	1698,153	3992,6602
7	432	361,2000	70,8000	5012,6351	61,7290	4456,375	15671,9102
8	445	416,8019	28,1981	795,1356	1814,9148	1996,428	19095,7852
9	367	424,1765	-57,1765	3269,1558	7288,8361	-1612,272	3622,5352
10	367	350,3247	16,6753	278,0653	5454,0914	-953,4352	3622,5352
11	321	345,3655	-24,3655	593,6761	1684,3439	-406,3013	201,2852
12	307	334,7235	-27,7235	768,5939	11,2765	675,4967	0,0352
13	331	386,7897	-55,7897	3112,4907	787,7102	1546,687	585,0352
14	345	352,0517	-7,0517	49,7263	2375,3939	393,4115	1458,2852
15	364	353,2302	10,7698	115,9879	317,6042	-75,94502	3270,4102
16	384	361,7251	22,2749	496,1704	132,3677	239,8953	5957,9102
	4909	4909,0000	0,0000	22360,1037	30336,2280	6811,9263	158718,4375

Рис. 21. Сравнение расчетного значения d-критерия Дарбина -Уотсона с критическими значениями вd_L и d_U

Так как расчетное значение d-критерия Дарбина-Уотсона попало в зону неопределенности, то нельзя сделать окончательный вывод об автокорреляции остатков по этому критерию.

Для определения степени автокорреляции вычислим коэффици­ент автокорреляции и проверим его значимость при помощи критерия стандартной ошибки. Стандартная ошибка коэффициента корреляции рассчитывается по формуле:

Коэффициенты автокорреляции случайных данных должны об­ладать выборочным распределением, приближающимся к нормаль­ному с нулевым математическим ожиданием и средним квадратическим отклонением, равным

Если коэффициент автокорреляции первого порядка r₁ находится в интервале

-1,96 * 0,25 < r₁ < 1,96* 0,25,

то можно считать, что данные не показывают наличие автокорреля­ции первого порядка.

Используя расчетную таблицу 9, получаем:

.

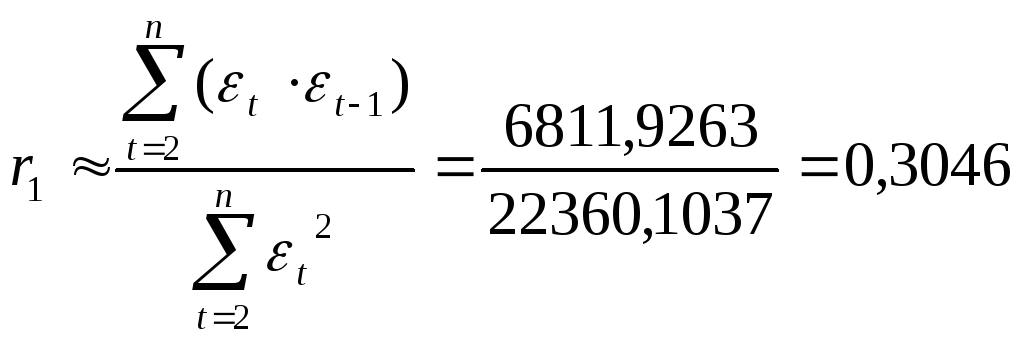Так как -0,49 < r₁ =0,3046 < 0,49, то свойство независимости остатков выполняется.

Вычислим для построенной модели множественный коэффици­ент детерминации

.

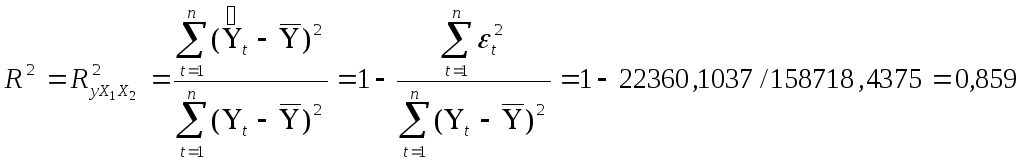Множественный коэффициент детерминации показывает долю вариации результативного признака под воздействием включенных в модель факторов Х₂ и Х₅. Т.о., около 86 % вариации зависимой пере­менной (объема реализации) в построенной модели обусловлено влиянием включенных факторов Х₂ (расходы на рекламу) и Х₅ (индекс потребительских расходов).

Проверку значимости уравнения регрессии проведем на основе F-критерия Фишера

.

Табличное значение F-критерия при доверительной вероятности 0,95, степенями свободы ₁=k=2 и ₂=(n-k-1)=16-2-1=13 составляет F_табл=3,8.

Поскольку

F_факт=39б599 F_табл=3,8,

то уравнение регрессии следует признать адекватным.

Значимость коэффициентов уравнения регрессии а₁ и а₂ оценим с использованием t-критерия Стьюдента:

t_a1=a₁/S_a1=9,5684/2,2659=4,2227,

t_a2=a₂/S_a2=15,7529/2,4669=6,3857.

Табличное значение t-критерия Стьюдента при уровне значимо­сти 0,05 и степенях свободы (16-2-1) = 13 составляет t_ma6n =2,16. Так как

t_a1=4,2227 t_ma6n =2,16,

t_a2=6,3857 t_ma6n =2,16,

то отвергаем гипотезу о незначимости коэффициентов уравнения регрессии а₁ и а₂.

Рассмотрим вопрос о влиянии факторов на зависимую переменную

Проанализируем влияние включенных в модель факторов на зависимую переменную по модели. Учитывая, что коэффициенты регрессии невозможно использовать для непосредственной оценки влия­ния факторов на зависимую переменную из-за различия единиц изме­рения, вычислим соответствующие коэффициенты эластичности, -коэффициенты:

,

,

.

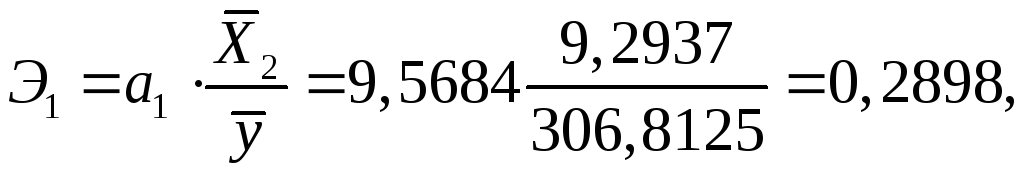
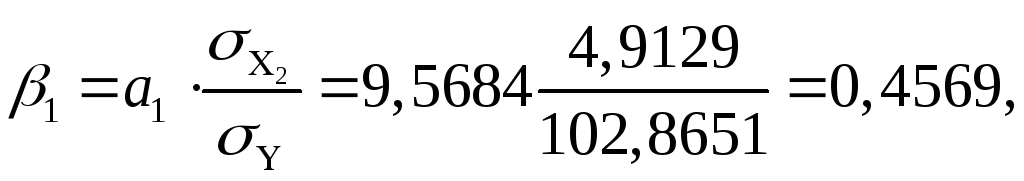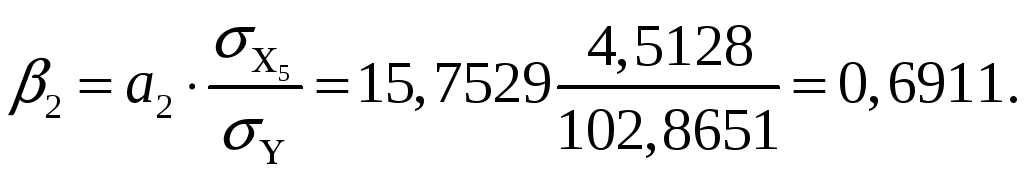Таким образом, при увеличении расходов на материл на 1 % величина объема реализации изменится приблизительно на 0,3 %, при увеличении расходов на 1 % величина объема реа­лизации изменится на 5,5 %.

Кроме того, при увеличении затрат на материалы на 4,9129 ед. объем реализации увеличится на 47 тыс. руб. (0,4569·102,865147), при увеличении расходов на 4,5128 ед. объем реализа­ции увеличится на 71 ед. (0,6911·102,865171).

Проведём процедуру прогнозирования с использованием точечных и интервальных характеристик.

Найдем точечные и интервальные прогнозные оценки объема реализации на два квартала вперед.

Для построения прогноза результативного признака Y и оценок прогноза необходимо определить прогнозные значения включенных в модель факторов Х₂ и Х₅. В п. 1.3 на рис. 10 приведен результат по­строения тренда и прогнозирования по тренду для временного ряда «Индекс расходов».

В качестве аппроксимирующей функции выбран полином второй степени - парабола:

Х₅ = 97,008 + 1,739 t - 0,0488 t²,

по которой построен прогноз на два шага вперед, причем прогнозные значения на 17-й и 18-й периоды соответственно составляют:

Х₅(17) = 97,008+1,739·17-0,0488·17²= 112,4678,

Х₅(18) = 97,008 +1,739·18-0,0488 18²= 112,4988.

Описанным способом (п. 1.3) построим линию тренда для временного ряда «Расходы на материалы» (рис. 22).

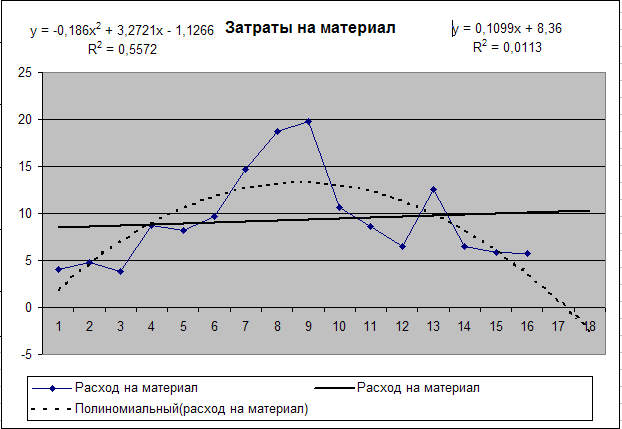
Рис. 22. Результат построения тренда и прогнозирования по тренду для временного ряда «Расходы на материал»

Для фактора Х₂ «затраты на материал» выбираем полиномиальную модель пятой степени (этой модели соответствует наибольшее значе­ние коэффициента детерминации):

Х₂= -0,00055157·t⁵ + 0,02915029·t⁴ - 0,55145744·t³ + +4,31897327·t² - 11,61564797·t + 12,83076923.

Замечание. Полиномы высоких порядков редко используются при прогнозировании экономических показателей. В этом случае при вычислении прогнозных оценок коэффициентов модели необходимо учитывать большое число знаков после запятой.

Прогнозные значения на 17-й и 18-й периоды соответственно составляют:

Х₂₍₁₇₎ = 5,7485,

Х₂₍₁₈₎ = 4,8485.

Для получения прогнозных оценок переменной 7 по модели

=-1471,3143 + 9,5684·X₂+15,7529·X₅

подставим в нее найденные прогнозные значения факторов Х₂ и Х₅, получим:

₍₁₇₎ =-1471,3143 + 9,5684·5,7485 + 15,7529·112,4678 = 355,3805,

₍₁₈₎ = -1471,3143 + 9,5684·4,8485 + 15,7529·112,4988 = 347,2573.

Доверительный интервал прогноза имеет границы:

верхняя граница прогноза: (n+l) + U(l),

нижняя граница прогноза: (n+l) - U(l),

где

, V_пр=X_пр^T(X^TX)^-1X_пр.

Имеем

,

t_кр=2,16 (по таблице при =0,05 и числе степеней свободы 13),

, .

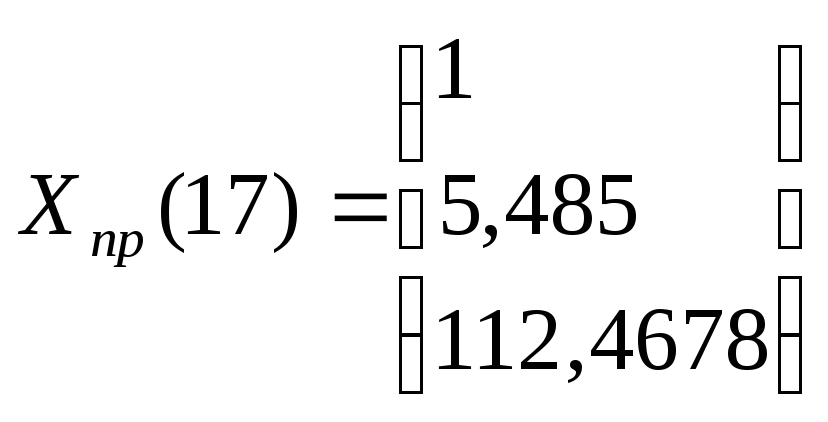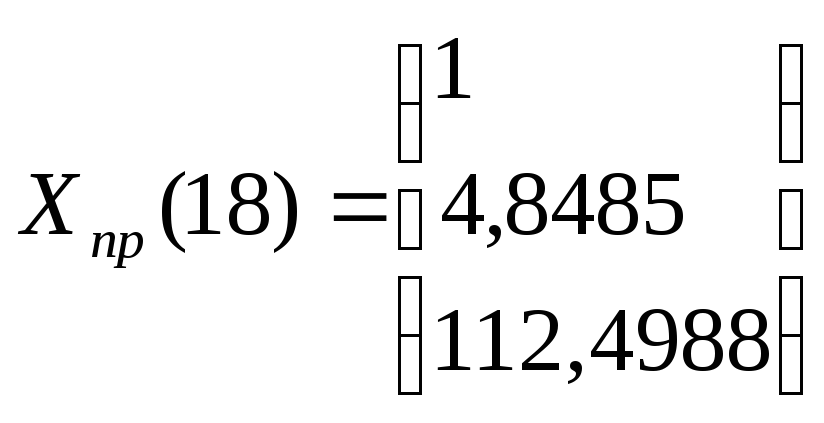Тогда с использованием Excel ,

имеем

V_пр(17)=X_пр^T(X^TX)^-1X_пр=0,2300,

U(1)=41,473*2,16*=42,9714

и

V_пр(18)=X_пр^T(X^TX)^-1X_пр=0,2613,

U(2)=41,473*2,16*=45,7964.

Результаты прогнозных оценок модели регрессии представим в таблице прогнозов (табл. 10).

Таблица 10

Упреждение	Прогноз	Нижняя граница	Верхняя граница
1	355,3805	312,4091	398,3520
2	347,2573	301,4609	393,0537