4. 4. Экономическая интерпретация многофакторной регрессионной модели

Анализ коэффициентов уравнения множественной регрессии: позволил сделать вывод о степени влияния каждого из двух факторов на показатель производительности труда.

Так, величина параметра а₁=-0,41 свидетельствует о том, что с увеличением продолжительности внутрисменных простоев на 1 мин следует ожидать снижения производительности труда (дневной выработки деталей одним рабочим) на 0,41 шт. (обратная связь). Повышение же квалификации рабочего на 1 разряд может привести к увеличению выработки на 3,37 детали. Отсюда можно сделать соответствующее практические выводы и осуществить мероприятия, направленные на повышение производительности труда.

Однако на основе коэффициентов регрессии нельзя сказать, какой из факторных признаков оказывает наибольшее влияние на результативный признак, так как коэффициенты регрессии между собой несопоставимы, поскольку они измерены разными единицами. На их основе нельзя также установить в развитии таких факторных признаков заложены наиболее крупные резервы изменения результативного показателя, потому что в коэффициентах регрессии не учтена вариация факторных признаков.

Чтобы иметь возможность судить о сравнительной силе влияния отдельных факторов и о тех резервах, которые в них заложены, должны быть вычислены частные коэффициенты эластичности , а также бета-коэффициенты .

Различия в единицах измерения факторов устраняют с помощью частных коэффициентов эластичности, которые рассчитывают по формуле:

,

где а_i- коэффициент регрессии при i-м факторе; х_i- среднее значение i-го фактора; -среднее значение изучаемого показателя.

Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется анализируемый показатель с изменением на 1% каждого фактора при фиксированном положении других факторов.

Для определения факторов, в развитии которых заложены наиболее крупные резервы улучшения изучаемого показателя, необходимо учесть различия в степени варьирования вошедших в уравнение факторов. Это можно сделать с помощью -коэффициентов, которые вычисляют по формуле:

, (60)

где -среднее квадратическое отклонение i-го фактора; -среднее квадратическое отклонение показателя; - коэффициент показывает на какую часть среднего квадратического отклонения измеряется результативный признак с изменением соответствующего факторного признака на величину его среднего квадратического отклонения.

Исходя из соотношения

и принимая во внимание, что коэффициент множественной детерминации R² есть доля изучаемых факторов в наличном приращении результативного показателя в анализируемой совокупности, можно сделать вывод, что произведение является показателем силы влияния соответствующего фактора на данный показатель.

Поделив произведение на коэффициент множественной детерминации R², получим коэффициент, который показывает, какова доля вклада анализируемого фактора в суммарное влияние всех отобранных факторов. Обозначив этот коэффициент , получим:

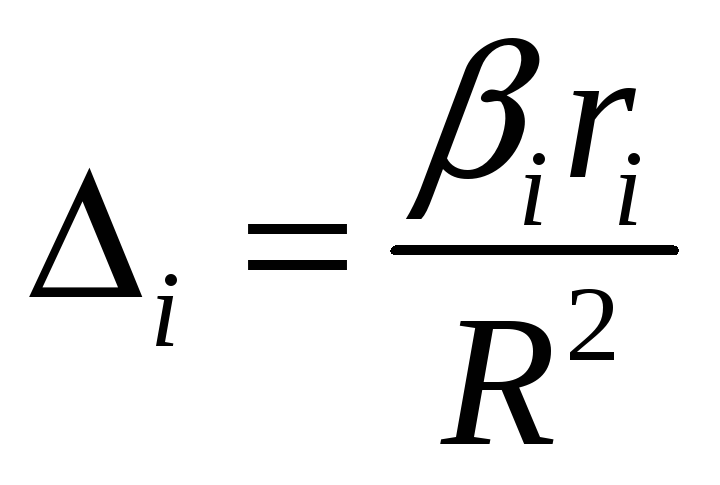, (61)

Рассчитаем для нашего примера коэффициенты эластичности Э_i, а также коэффициенты и , дадим им экономическую интерпретацию:

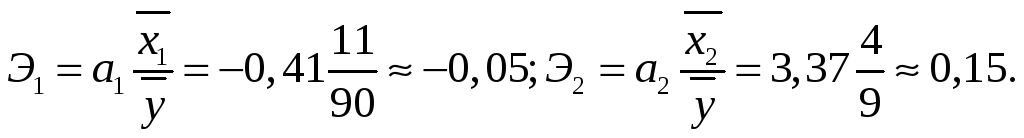
Анализ частных коэффициентов эластичности показывает, что по абсолютному приросту наибольшее влияние на производительность труда оказывает фактор Х₂- повышение квалификации рабочих на 1 % приводит к росту производительности труда на 0,15%.Снижение же продолжительности внутрисменных простоев на 1% повышает производительность труда только на 0,05%:

Анализ β_i – коэффициентов показывает, что на производительность труда наибольшее влияние из двух исследуемых факторов с учетом уровня их вариации способен оказать фактор х₂ – квалификация рабочих, так как ему соответствует наибольшее (по абсолютной величине) значение β-коэффициента

На основании анализа _i-коэффициентов установлено, что наибольшая доля прироста производительности труда из двух анализируемых факторов может быть обеспечена развитием такого фактора, как повышение квалификации рабочих.

Таким образом, на основании частных коэффициентов эластичности Э_i,β_i- и _i- коэффициентов можно судить о резервах роста производительности труда, которые заложены в том или ином факторе. [9, с.86]

РЕЗЮМЕ

Регрессия – это функция, которая наилучшим образом соответствует исходным данным. Математическое описание зависимости в среднем изменений переменной у от х называется уравнением парной регрессии.

Математически корреляционная зависимость результативной переменной от нескольких факторных (объясняющих) переменных описывается уравнением множественной регрессии.

Уравнение множественной регрессии характеризует среднее изменение у с применением признаков-факторов.

Не рекомендуется включать совместно признаки, представленные как абсолютные и средние или относительные величины. Нельзя включать в регрессию признаки, функционально связанные с зависимой переменной у, например те, которые являются составной частью у.

При использовании регрессий в решении конкретной задачи убедитесь, что выполнены следующие условия построения регрессии:

• исходные данные однородны;

• число рассматриваемых переменных не слишком велико: для получения надежных оценок коэффициентов регрессии число объясняющих переменных должно быть не менее чем в 6 раз меньше числа наблюдений, .

Если уравнение регрессии статистически значимо, на его основе можно проводить расчет ожидаемых значений результата при заданных значениях факторов. Если статистически значимы параметры уравнения регрессии, то на его основе можно рассчитывать ожидаемые значения результата для отдельных единиц совокупности. [2]

В этой главе приведено:

▼ ▲	Приёмы построения уравнения регрессии. Проверка адекватности регрессионной модели. Построение и статистический анализ двухфакторной линейной модели (трехмерной регрессии). Экономическая интерпретация многофакторной регрессионной модели.

_____________________________________________