2.5. Корреляционный анализ порядковых переменных или ранговая корреляция
Рассмотренные методы корреляционного анализа предназначены для количественных переменных. В социально-экономических исследованиях встречаются ситуации, когда признак не выражается количественно, однако единицы совокупности можно упорядочить. Такое упорядочение единиц совокупности называется ранжированием. Примером может служить ранжирование совокупности людей по уровню образования.
При ранжировании каждой единице совокупности присваивается ранг - порядковый номер в упорядоченном ряду. При совпадении значения признака у различных единиц им присваивается одинаковый ранг, равный среднему арифметическому из номеров их мест. Такие ранги называются связанными.
Так, на 4-м и 5-м месте стоят единицы с одинаковым значением признака. Тогда каждой из них присваивается ранг, равный (4+5)/2 = 4,5. Следующей за ними единице присваивается ранг, равный 6.
Связь между рангами переменных определяется коэффициентом корреляции рангов. Ранговые коэффициенты корреляции относятся к числу непараметрических статистик и позволяют измерить силу связи между количественными признаками, форма распределения которых отличается от нормальной.
Наиболее распространенными мерами связей между порядковыми переменными являются коэффициенты корреляции рангов Спирмэна и Кендэлла.
Рассмотрим применение коэффициента корреляции рангов Спирмэна
Формула коэффициента корреляции рангов Спирмэна получена из формулы коэффициента парной корреляции:
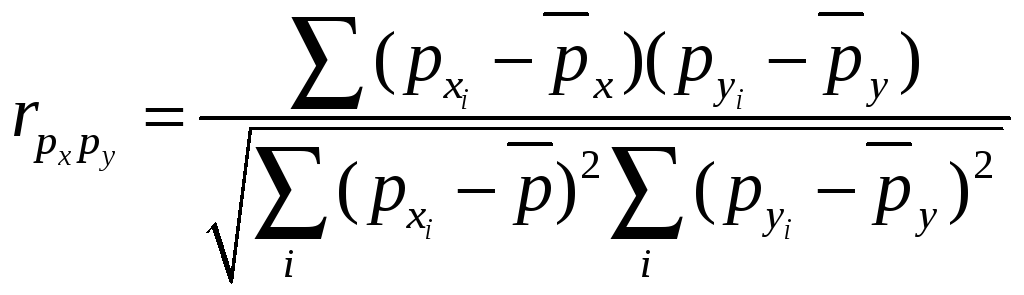, (19)
где
- ранг i-й
единицы совокупности по переменной х;
-
средний ранг по переменной х;
- ранг
i-й
единицы совокупности по переменной у,
средний
ранг по переменной у.
Очевидно, что коэффициент ранговой корреляции изменяется, так же, как и коэффициент парной корреляции, в интервале от -1 до +1.
При отсутствии связанных рангов путем преобразований приведенной формулы Спирмэном была получена формула коэффициента ранговой корреляции, который обычно обозначается греческой буквой p:
,
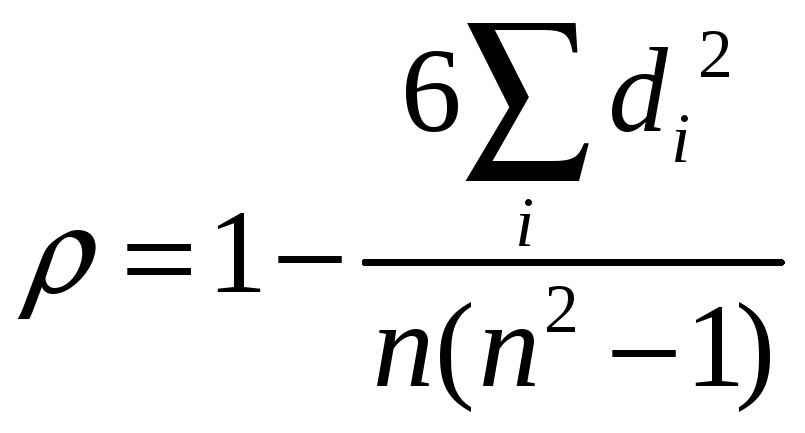(20)
где di – разность рангов по переменным х и у для i-й единицы совокупности; n- число наблюдений.
Ранговый коэффициент корреляции изменяется, так же как и коэффициент парной корреляции, в интервале от -1 до +1 и оценивает силу линейной зависимости между рангами.
При наличии связанных рангов необходимо пользоваться скорректированной формулой коэффициента корреляции рангов Спирмэна. Пусть определяется теснота связи между к-м и l-м признаками, в рядах значений которых имеется соответственно q и g групп объединенных рангов. Тогда формула коэффициента корреляции рангов Спирмэна примет вид
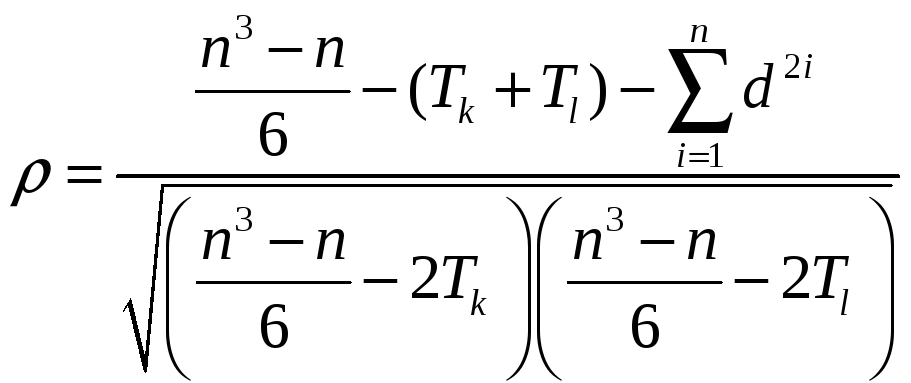, (21)
где
,
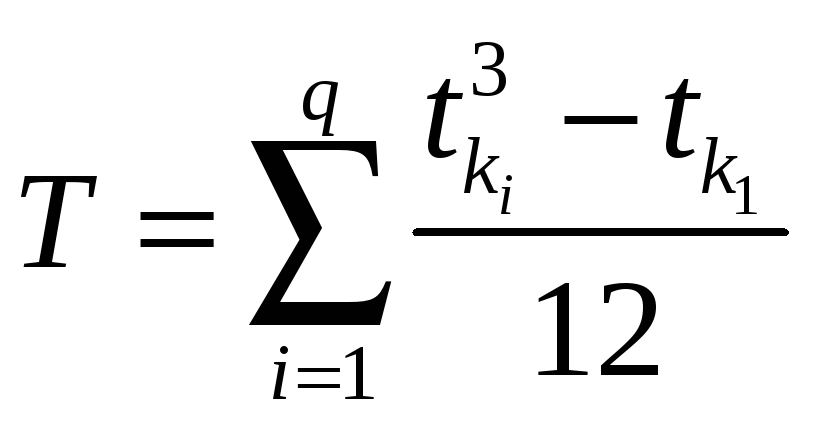(22)
,
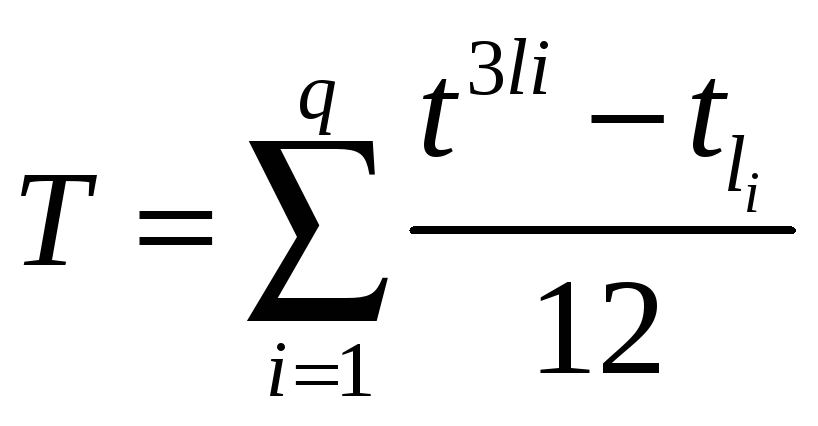(23)
где t и tli – число единиц в i-й группе объединенных рангов соответствующего признака.
Статистическая значимость коэффициентов корреляции Спирмэна проверяется с помощью специальных таблиц.
Если абсолютная величина расчетного значения рангового коэффициента корреляции больше табличного, нулевая гипотеза отвергается и корреляция признается статистически значимой.