9. Спектры периодических сигналов.

Периодические сигналы конечно не существуют, т.к. любой реальный сигнал имеет начало и конец. Однако при анализе сигналов в установившемся режиме можно считать, что они существуют бесконечно долго и принять в качестве математической модели таких сигналов периодическую функцию времени. Они могут быть как в виде экспоненциальных составляющих, так и в виде гармоничных.

Пусть функция u(t) заданная на интервале [t₁, t₂] (t_{1 } t _ t₂) и удовлетворяющая условию Дирихле, повторяется с периодом на протяжении времени 0 - до +.

Условие Дирихле: на любом конечном интервале функция должна быть непрерывной или иметь конечное число точек разрыва первого рода, а также конечное число экстремальных точек.

В точках разрыва t₀ функцию u(t) следует считать равной

Если в качестве базисных выбраны экспоненциальные функции то выражение (5) запишется в виде:

(15)

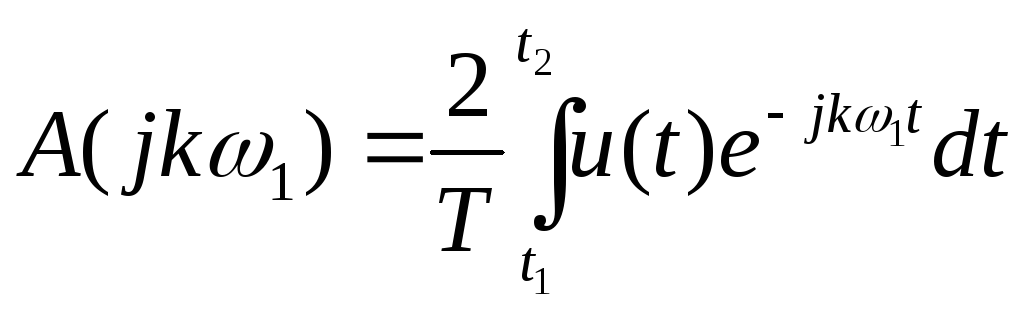(16)

Соотношение (15) представляет собой ряд Фурье в комплексной форме, содержащей экспоненциальные функции, как с положительным, так и с отрицательным параметром  (двустороннее частотное представление). Составляющие с отрицательными частотами являются следствием комплексной формы записи вещественной функции.

Функцию A(jk₁) называют комплексным спектром периодического сигнала u(t). Этот спектр дискретный, т.к. функция A(jk₁) определена на числовой оси только для целых значений k. Значение A(jk₁) при конкретном k называют комплексной амплитудой.

Огибающая комплексного спектра A(j) имеет вид:

(17)

Запишем комплексный спектр в форме:

(18)

Модуль комплексного спектра A(k₁) называют спектром амплитуд, а функцию (k₁) – спектром фаз. Если известны A(k₁) и (k₁), то в соответствии с (15) сигнал u(t) восстанавливается однозначно. Более важен параметр A(k₁).

Поскольку A(k₁) и (k₁) отличны от нуля только при целых k, спектры амплитуд и фаз периодического сигнала являются дискретными.

Воспользовавшись формулой Эйлера

выразим комплексный спектр A(jk₁) в виде действительной и мнимой частей:

(19)

где (20)

(21)

Спектр амплитуд

(22)

является четной функцией k, т.е.

(23)

Поскольку четность А_k и В_k противоположна, спектр фаз - функция нечетная, т.е.

(k₁) = - (-k₁) (24)

При k=0 получаем постоянную составляющую

(25)

От двустороннего спектрального представления легко перейти к одностороннему (не имеющему отрицательных частот), объединяя комплексно-сопряженные составляющие [см.(14)]. В этом случае получается ряд Фурье в тригонометрической форме.

Действительно, выделив в (15) постоянную составляющуюА₀/2 и суммируя составляющие симметричных частот  и -, имеем

(26)

учитывая (17) и (18) запишем

или

Воспользовавшись формулой Эйлера (14) и обозначив (k₁) через _k, окончательно получим

(27)

Рассмотрена и другая тригонометрическая форма ряда Фурье, имеющая вид

(28)

Однако она менее удобна для практического применения.

Отдельные составляющие в представлениях (27) и (28) называют гармониками. Спектр амплитуд и фаз представляют спектральными диаграммами. Диаграмма спектра амплитуд представлена на рисунке 5.

Огибающую A() этого спектра амплитуду можно получить, заменив k₁ в A(k₁) на ₁, где  = k₁ для k–й гармоники.

Поскольку спектры отображаются совокупностью линий, их часто называют линейчатыми. Аналогично представляются спектры фаз.