7.1 Первый канал возмущения

Передаточная функция по первому каналу возмущения имеет вид:

, гдеk = 0,5; b_1.1 = 1;

Передаточная функция замкнутой системы по первому каналу возмущения имеет вид:

, где ;

Получим:

;

S0 и S1 - оптимальные настройки ПИ-регулятора при =0

S1=1.026, S2=0.005051, b₁=5, K=1

В передаточной функции замкнутой системы заменим р на j

где

;

;

График для вещественной частотной характеристики замкнутой системы по первому каналу возмущения представлен на рис. 50.

Рисунок 50 – ВЧХ по первому каналу возмущения

Рассчитаем переходный процесс по первому каналу возмущения с помощью следующего выражения:

;

Данные для построения переходного процесса по первому каналу возмущения представлены в таблице 7.1

Таблица 7.1

t	0	10	20	40	60	80	100	120	140
h(t)	0	0.216	0.585	0.371	0.356	0.324	0.295	0.266	0.24

Переходный процесс изображён на рис. 51.

Рисунок 51 – Переходный процесс по первому каналу возмущения

7.2 Второй канал возмущения

где k = 0,5; b_1.2 = 6; τ = 3

S0 и S1 - оптимальные настройки ПИ-регулятора при =0

S1=1.026, S2=0.005051, b₁=5, K=1;

Формула для вещественной частотной характеристики замкнутой системы по каналу возмущения выведена в предыдущем пункте и имеет вид:

, где

;

;

График ВЧХ замкнутой системы по второму каналу представлен на рис. 52.

Рисунок 52 – ВЧХ по второму каналу возмущения

Рассчитаем переходный процесс по второму каналу возмущения с помощью следующего выражения:

;

Данные для построения переходного процесса по первому каналу возмущения представлены в таблице 7.2

Таблица 7.2

t	0	5	10	15	20	25	30	40	60
h(t)	0	0.116	0.01	-0.05	0.032	-0.008	-0.01	-0.004	0

Переходный процесс изображён на рис. 53.

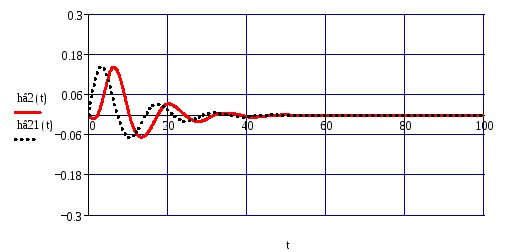
Рисунок 53 – Переходный процесс по второму каналу возмущения при наличии(сплошная линия) и отсутствие запаздывания (пунутир).

7.3 Третий канал возмущения

, где k = 0,5; b_3.2 = 400; b_3.1 = 32; τ = 10;

;

;

S0 и S1 - оптимальные настройки ПИ-регулятора при =0

S1=1.026, S2=0.005051, b₁=5, K=1;

, где

;

;

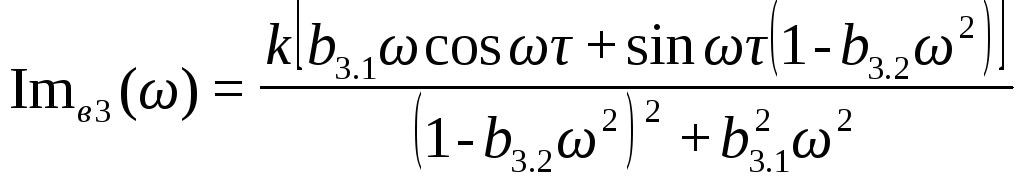График ВЧХ замкнутой системы по третьему каналу возмущения изображён на рис. 54.

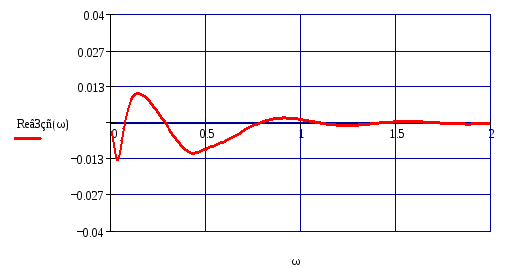
Рисунок 54 – ВЧХ по третьему каналу возмущения

Рассчитаем переходный процесс по второму каналу возмущения с помощью следующего выражения:

;

Данные для построения переходного процесса по первому каналу возмущения представлены в таблице 7.3

Таблица 7.3

t	0	10	20	30	40	50	60	80	100
h(t)	0	0.004	-0.006	-0.01	-0.01	-0.009	-0.007	-0.003	-0.002

Переходный процесс по третьему каналу возмущения при отсутствии запаздывания по каналу управления представлен на рис. 55.

Рисунок 55 – Переходный процесс по третьему каналу возмущения

8 Определение нулей и полюсов передаточных функций замкнутой системы.

Для получения корневых показателей качества системы управления необходимо рассчитать корни полиномов числителя и знаменателя передаточной функции замкнутой системы для случаев, когда запаздывание в канале регулирования равно нулю. Для этого необходимо в общие функции замкнутой системы подставить конкретные выражения передаточных функций объекта и регулятора и привести Wзс(p) к отношению произведений полиномов.

Определение полюсов передаточной функции необходимо производить для каждого сомножителя характеристического полинома отдельно.