11

Задание на курсовую работу.

1) По функциональной схеме составить передаточные функции элементов и структурную схему системы регулирования. Описать процессы регулирования.

2) Определить передаточные функции замкнутой системе по команде, по ошибке, характеристические уравнения разомкнутой и замкнутой системы.

3) Построить области устойчивости замкнутой системы методом D-разбиения по неизвестному коэффициенту усиления. Коэффициент выбрать из предполагаемой области устойчивости и определить устойчивость по корням характеристического уравнения, по критериям Гурвица, Михайлова и Найквиста. Определить запасы устойчивости по амплитуде и по фазе.

4) Выбрать коэффициент усиления системы из условия требуемой точности и построить ЛАХ и ЛФХ разомкнутой исходной системы.

5) Построить желаемую ЛАХ из условия обеспечения требуемых значений быстродействия t_рег и перерегулирования .

6) Определить ЛАХ и передаточную функцию корректирующего устройства и скорректированной системы.

7) Определить место включения, тип и параметры корректирующих звеньев на основе

R-C элементов и операционных усилителей. Нарисовать структурную схему системы с корректирующими звеньями.

8) Определить статическую, скоростную и по ускорению ошибки скорректированной системы, по ЛАХ и ЛФХ – запасы устойчивости по амплитуде и по фазе. Сравнить их с аналогичными характеристиками исходной системы.

9) Построить переходную характеристику управляемого сигнала спроектированной системы и определить показатели качества переходного процесса.

10) Привести постановку, задачу, методы, использованные в работе, технические характеристики спроектированной системы, сравнив их с характеристиками исходной, сделать выводы о проделанной работе.

Функциональная схема системы

и уравнения, описывающие систему.

Следящая система включает датчик рассогласования, выполненный на сельсине-датчике СД и сельсине-приемнике СП, работающих в трансформаторном режиме, предварительный усилитель У₁, усилитель мощности У₂, исполнительный двигатель Д, осуществляющий через редуктор Р поворот исполнительной оси управляемого объекта. С этой же осью механически связан ротор сельсина-приемника СП.

Датчик рассогласований: U₁=1.5(a₀–a₂)

У₁: U₂=K₁U₁

У₂: 0,03+U₃=5U₂

Р: а₂=а₁

Д: 0,05+0,2+=3U₃

1. Передаточные функции элементов

и структурная схема системы регулирования.

Учитывая, что , получаем:

Датчик рассогласований: U₁=1.5(a₀–a₂)

У₁: U₂=K₁U₁

У₂: 0,03pU₃+U₃=5U₂

Р: а₂=а₁

Д: 0,05p³а₁+0,2p²а₁+pа₁=3U₃

Передаточная функция звена – это отношение собственного оператора к оператору воздействия. Тогда

W_расс=1,5

W_у1=

W_у2=

W_Д=

W_p=

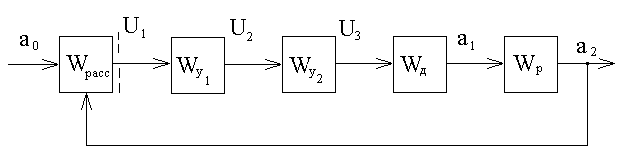
В следящей системе помещено устройство слежения за изменениями внешнего фактора. Регулируемой величиной является угол поворота управляемого объекта. Входное воздействие подается на сельсин-датчик в виде угла поворота его ротора. Соединенный по трансформаторной схеме сельсин-датчик и сельсин-приемник вырабатывают напряжение, пропорциональное рассогласованию между входным и выходным валами следящей системы. Напряжение ошибки усиливается усилителями У₁ и У₂ и поступает на якорь исполнительного двигателя, вращающего одновременно нагрузку и ротор сельсина-приемника до тех пор, пока рассогласование не станет равным нуля. Таким образом, поддержание постоянной величины происходит непрерывно.

2. Передаточные функции замкнутой системе по команде,

по ошибке, характеристические уравнения разомкнутой

и замкнутой системы.

W_П(p)=

W_П(p)= –передаточная функция прямой цепи

W_З(p)=

W_З(p)= – передаточная функция замкнутой цепи по команде

W_З(p)=

W_З(p)= – передаточная функция замкнутой цепи по ошибке

W_раз(p)= W_П(p)

W_раз(p)= – передаточная функция разомкнутой цепи

p(p²+4p+20)(3p+100)==0 – характеристическое уравнение разомкнутой цепи

=0 – характеристическое уравнение замкнутой цепи

3. Построение областей устойчивости замкнутой системы методом D-разбиения по неизвестному коэффициенту усиления.

где x=K₁– неизвестный коэффициент усиления

3p⁴+112p³+460p²+2000p+150K₁ – характеристическое уравнение замкнутой системы в зависимости от К₁

R(p)= 3p⁴+112p³+460p²+2000p

Q(p)= 150

=

X()=(–0.02⁴+3.066²)

Q()=(0.746³–13.33)

Из графика видно, что K_1max48, следовательно, K₁ можно взять примерно 38.

Определение устойчивости по корням характеристического уравнения.

Ниже представлена матрица корней характеристического уравнения, из которой видно, что вещественная часть всех корней отрицательна, что является необходимым и достаточным условием устойчивости системы.

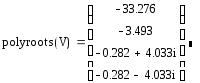
Определение устойчивости по критерию Гурвица:

–главный определитель Гурвица

a₀=3, 112,45520,19539200,111373440000

Определители Гурвица низшего порядка имеют тот же знак, что и a₀, следовательно, система устойчива.

Определение устойчивости по критерию Михайлова:

Способ № 1:

D(p)=3p⁴+112p³+460p²+2000p+5700=0 – характеристическое уравнение системы

Подставляем p=j и находим вещественную и мнимую функции Михайлова:

X()=3⁴–460²+5700=0

Y()=(–112²+2000)=0

Корни уравнения Y()=0 ₁=0, ₂=4,225

Подставляя ₁ и ₂ в X(), получаем

X(₁)=5700

X(₂)=–1555

Так как все корни Y() вещественны и знаки ординат X(), соответствующие этим корням, чередуются, то, по критерию Михайлова, система устойчива.

Способ № 2:

D(p)=– характеристическое уравнение замкнутой цепи.

Заменив pнаj, получаем функциюD(j), откуда

X()=Re(D(j))=3⁴–460²+5700

Y()=Im(D(j))=–112³+2000

, с-1	0	1	2	3	4	5	6	7	8
X()	5700	5243	3908	1803	-892	–3925	–6972	–9637	–11450
Y()	0	1888	3104	2976	832	–4000	–12190	–24420	–41340
, с-1	9	10	11	12	13	14	15	20	25
X()	–11880	–10300	–6037	1668	13640	30790	54070	301700	890100
Y()	–63650	–92000	–127100	-169500	–220100	–279300	–348000	–856000	–1700000

При  X(), Y() –

Кривая проходит последовательно четыре квадрантанта, следовательно, система устойчива, так как характеристическое уравнение содержит четвертую максимальную степень.

Определение устойчивости по критерию Найквиста:

–передаточная функция разомкнутой цепи

Заменивpнаj, получаем

, откуда

	0.3	0.8	1	2	3	4	4.225	5	12.38
X()	–0.017	–0.018	–0.018	–0.021	–0.024	–0.022	–0.021	–0.013	0
Y()	–0.25	–0.094	–0.075	–0.036	–0.019	–0.0028	0	0.0055	0.0008

Построив годограф АФЧХ, мы видим, что он не огибает точку (–1; 0), следовательно, по критерию Найквиста система устойчива.

Запасы устойчивости по амплитуде и по фазе.

При _ср=–1,42510^-3W(j_ср)=1,(_ср)=52,632. Следовательно, запас по устойчивости по фазе=–(_ср)=127,638, а запас по амплитуде равен 0,78 – отрезку, заключенному между точкой (–1; 0) и АФЧХ.