83

Содержание

6.1 Построение переходного процесса с выбранными оптимальными настройками 49

6.2 Построение переходного процесса с настройками выбранными левее оптимальных. 51

6.3 Построение переходного процесса с настройками выбранными правее оптимальных. 52

7 Построение переходных процессов в замкнутой системе по каналам возмущения при τ = 0 55

10.1 Вывод формул для расчета настроек ПД- регулятора – S2 и S1 66

10.2 Выбор пар настроек ПД- регулятора. 67

Список используемой литератуы 83

Задачи курсовой работы по теории автоматического управления

Курсовая работа посвящена анализу и синтезу одноконтурных систем автоматического управления (САУ) и состоит из следующих основных разделов:

1. анализ динамических свойств объекта управления во временной и частотной областях;

2. синтез замкнутой системы автоматического управления с пропорционально-интегральным регулятором, со степенью колебательности m=0,221;

3. построение переходных процессов в замкнутой системе автоматического управления по различным каналам с целью анализа ее качества;

4. синтез замкнутой системы автоматического управления с пропорционально-дифференциальным регулятором, со степенями колебательности m₁=0,147 и m₂=0,336;

5. построение переходных процессов в замкнутой системе автоматического управления с пропорционально-интегральным регулятором по одному из каналов возмущения с целью анализа ее качества

Исходные данные

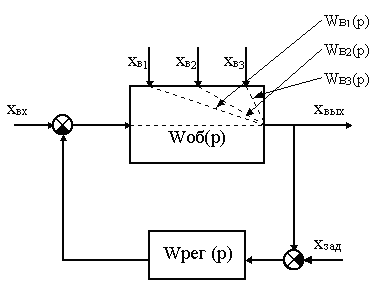
Рисунок 1 – Структурная схема системы автоматического управления

а) Вид передаточной функции по каналу регулирования:

, где k = 1; b₁ = 5; τ = 1.

б) Вид передаточной функции по первому каналу возмущения:

, где k = 0,5; b₁ = 1; τ = 0.

в) Вид передаточной функции по второму каналу возмущения:

, где k = 0,5; b₁ = 6; τ = 3.

г) Вид передаточной функции по третьему каналу возмущения:

, где k = 0,5; b₂ = 400; b₁ = 32; τ = 10.

Анализ и синтез замкнутой системы управления необходимо провести:

а) с ПИ-регулятором на заданную степень колебательности m=0,221.

б) с типом регулятора и условиями расчета его настроек, выбираемыми по номеру варианта регулятора.

Номер варианта регулятора – 3:

Регулятор ПД, выбрать три пары настроек S₁ – S₂ c кривой равной степени колебательности m=0,221 в области положительных значений настроек и диапазоне частот до частоты среза.

1. Анализ динамических свойств объекта во временной и частотной областях

1.1 Канал регулирования

, где k = 1; b₁ = 5; τ = 1

1.1.1 Построение переходного процесса:

Переходную функцию получаем при ступенчатом входном воздействии без учета чистого транспортного запаздывания, которое учтем в окончательной формуле. Расчет удобно проводить методом неопределённых коэффициентов в два этапа.

;

Разложим изображение на простые дроби:

Найдём неизвестные коэффициенты разложения:

При :

При :

При :

Тогда: ;;;

Следовательно

;

Используя обратное преобразование Лапласа, получим оригинал переходной функции:

;

Учитывая запаздывание получаем:

;

Подставляя в полученную формулу k =1; b₁ =5; τ =1, получаем переходную функцию по каналу регулирования:

;

Данные для построения переходного процесса по каналу регулирования представлены в таблице 1.1.

Таблица 1.1

t	0	2.5	5	7.5	10	12.5	15	17.5	20
h(t)	0	0.217	1.233	2.887	4.827	7.02	9.327	11.733	14.161

График переходного процесса по каналу регулирования представлен на рис. 2.

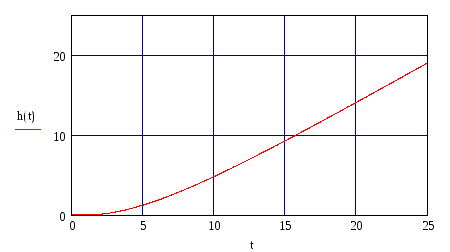
Рисунок 2 – переходная функция по каналу регулирования.

1.1.2 Построение амплитудо-частотной характеристики:

Выражение для АЧХ:

;

;

;

(1.2)

Подставляя в 1.2 исходные данные (k=1; b₁=5; τ=1) получим:

;

Данные построения АЧХ канала регулирования представлены в таблице 1.2.

Таблица 1.2.

ω	0.1	0.25	0.5	0.75	1.0	1.25	1.5	1.75	2.0
А(ω)	10	2.499	0.737	0.345	0.193	0.125	0.08	0.065	0.049

График АЧХ по каналу регулирования представлен на рис. 3.

Рисунок 3 – АЧХ по каналу регулирования.

1.1.3 Построение фазо-частотной характеристики.

==

(1.3)

Подставляя в (1.3) исходные данные ( b₁=5; τ=1)получим:

;

Данные построения ФЧХ канала регулирования представлены в таблице 1.3.

Таблица 1.3.

ω	0	0.5	1.0	1.5	2.0	2.5	3.0	3.5	4.0
(ω)	-1.57	-3.25	-3.93	-4.51	-5.01	-5.57	-6.07	-6.58	-7.01

График ФЧХ по каналу регулирования представлен на рис.4.

Рисунок 4 – ФЧХ по каналу регулирования.

1.1.4 Амплитудо-фазовая характеристика.

Чтобы получить амплитудно-фазовую характеристику объекта по каналу регулирования, необходимо получить выражения для вещественной и мнимой составляющихW_об(j). Для этого числитель и знаменатель выражения частотной передаточной функции умножим на выражение, сопряженное со знаменателем:

;

;

;

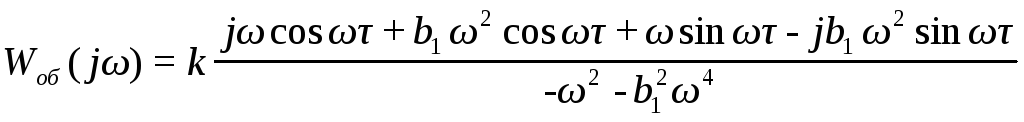
Для упрощения построения амплитудно-фазовой характеристики воспользуемся формулами:

;

;

; ;

Данные построения АФХ канала регулирования представлены в таблице 1.4.

Таблица 1.4.

Re	-5.98	-5.64	-4.78	-2.95	-0.74	-0.258	-0.136
Im	-99.69	-18.56	-7.56	-1.95	-0.089	0.16	0.141
ω	0.01	0.05	0.1	0.2	0.5	0.8	1

График АФХ по каналу регулирования представлен на рис. 5.

Рисунок 5 –АФХ по каналу регулирования.

1.2 Первый канал возмущения

, где k = 0,5; b₁ = 1; τ = 0

Передаточные функции по первому каналу возмущения и по каналу регулирования совпадают, по этому для построения графиков АЧХ, ФЧХ, переходной функции и АФХ, воспользуемся уже имеющимися формулами.