
- •I. Введение в анализ.
- •Предел функции в точке и на бесконечности. Геометрическая интерпретация. Теорема о единственности предела.
- •Бесконечно малые и бесконечно большие функции, их свойства
- •Теорема о связи функции с её пределом в точке
- •Алгебраические свойства пределов
- •Первый замечательный предел
- •Понятие предела последовательности. Теорема существования предела последовательности
- •Сравнение функций.
- •8. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции. Таблица эквивалентности
- •9. Понятие непрерывной функции в точке. Свойства непрерывных в точке функций
- •Свойства Локальные
- •Глобальные
- •10.Односторонние пределы функции в точке. Точки разрыва и их классификация.
- •Односторонний предел по Гейне
- •11.Основные теоремы о непрерывных на отрезке функциях
- •11. Дифференциальное исчисление функций одной перемен-
- •Правила дифференцирования функций
- •Производная сложной, обратной, параметрически заданной функции
- •Понятие дифференциала функции и его геометрический смысл. Применение дифференциала к приближенным вычислениям
- •Основные теоремы о дифференцируемых функциях (т.Ролля, Лагранжа, Коши)
- •Производные и дифференциалы высших порядков
- •Правило Лопиталя раскрытия неопределенностей. Раскрытие показательных неопределенностей
- •Формула Тейлора с остаточным членом в форме Лагранжа и Пеано
- •Разложение основных функций по формуле Тейлора
- •Монотонные функции. Признаки возрастания (убывания) функции на интервале
- •Понятие экстремума функции в точке. Необходимое и достаточное условия экс тремума функции в точке
- •Исследование функций на экстремум с помощью высших производных
- •Наибольшее и наименьшее значения функции на отрезке
- •Выпуклость и вогнутость графика функции, точка перегиба. Необходимое и достаточное условия точки перегиба графика функции
- •Понятие асимптоты графика функции. Нахождение вертикальных и наклонных асимптот
- •Полное исследование функции и построение графика функции
- •III. Неопределенный интеграл.
- •Понятие первообразной и ее свойства. Теорема о множестве первообразных
- •30.Таблица неопределенных интегралов основных функций
- •Интегрирование по частям и заменой переменной в неопределенном интеграле
- •Интегрирование функций с квадратным трехчленом в знаменателе
- •Интегрирование рациональных дробей методом разложения на простые дроби
- •Рекуррентные формулы. Вычисление интеграла
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций. Универсальная подстановка. Некоторые частные случаи
- •1.4 Интегрирование тригонометрических функций.
- •37.Интегралы, содержащие квадратичную иррациональность, и их вычисление с помощью тригонометрических подстановок
- •IV. Определенный интеграл.
- •Понятие определенного интеграла, его геометрический смысл, свойства
- •Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница
- •Интегрирование по частям и заменой переменной в определенном интеграле
- •Для неопределённого интеграла
- •Для определённого
- •Несобственные интегралы I и п рода. Определение, свойства, теоремы сравнения
- •Несобственные интегралы I рода
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •Несобственные интегралы II рода
- •Геометрический смысл несобственных интегралов II рода
- •Геометрические приложения определенного интеграла:
- •43. Физические приложения определенного интеграла (работа переменной силы при прямолинейном перемещении материальной точки, давление жидкости на пластинку).
- •V. Функции многих переменных.
- •44. Функции многих переменных (фмп). Область определения, предел в точке, непрерывность
- •2. Предел функции.
- •Понятие частной производной фмп. Правила дифференцирования
- •Дифференцирование сложной функции многих переменных. Формула для производной неявно заданной функции одной переменной
- •Касательная плоскость и нормаль к поверхности
- •Частный и полный дифференциалы фмп. Применение дифференциала к приближенным вычислениям
- •Частные производные высших порядков. Теорема о равенстве смешанных производных
- •Дифференциалы высших порядков
- •Формула Тейлора для функции двух переменных
- •Различные формы остаточного члена
- •Экстремумы фмп. Необходимое и достаточное условия экстремума фмп в точке
- •Постановка задач на экстремум. Нахождение наибольшего и наименьшего значений функции в замкнутой области
8. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции. Таблица эквивалентности
Эквивалентные бесконечно малые функции.
Если
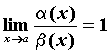 ,
то бесконечно малые функции
,
то бесконечно малые функции
![]() и
и
![]() называются
эквивалентными,
обозначают
называются
эквивалентными,
обозначают![]() ~
~![]() . Как
известно, сумма, разность и произведение
двух б.м.ф. есть функция бесконечно
малая. Отношение же двух б.м.ф. может
вести себя различным образом: быть
конечным числом, быть бесконечно большой
функцией, бесконечно малой или вообще
не стремиться ни к какому пределу.
. Как
известно, сумма, разность и произведение
двух б.м.ф. есть функция бесконечно
малая. Отношение же двух б.м.ф. может
вести себя различным образом: быть
конечным числом, быть бесконечно большой
функцией, бесконечно малой или вообще
не стремиться ни к какому пределу.
Две б.м.ф. сравниваются между собой с помощью их отношения.
Пусть α=α(х) и ß=ß(х) есть б.м.ф. при х→хо, т. е.
![]() и
и
![]()
1.
Если
![]() =А
0 (АєR), то α и ß называются бесконечно
малыми одного порядка.
=А
0 (АєR), то α и ß называются бесконечно
малыми одного порядка.
2.
Если,
![]() =0,
то α називатся бесконечно малой более
высокого порядка , чем ß.
=0,
то α називатся бесконечно малой более
высокого порядка , чем ß.
3.
Если
![]() =∞,
то α называется бесконечно малой более
низкого порядка, чем ß.
=∞,
то α называется бесконечно малой более
низкого порядка, чем ß.
4.
Если
![]() не
существует, то α и ß называются несравнимыми
бесконечно малыми.
не
существует, то α и ß называются несравнимыми
бесконечно малыми.
Отметим, что таковы же правила сравнения б.м.ф. при х →±∞, х →х0±0.
Таблица
эквивалентных бесконечно малых.
Пусть
![]() -
бесконечно малая при
-
бесконечно малая при
![]() .
.

9. Понятие непрерывной функции в точке. Свойства непрерывных в точке функций
ε-δ определение
Пусть
![]() и
и
![]() .
.
Функция f
непрерывна
в точке
![]() ,
если для любого ε
> 0 существует
δ > 0
такое, что
,
если для любого ε
> 0 существует
δ > 0
такое, что
![]()
Функция f непрерывна на множестве E, если она непрерывна в каждой точке данного множества.
В этом случае
говорят, что функция f
класса C0
и пишут:
![]() или,
подробнее,
или,
подробнее,
![]() .
.
-
Из определения следует, что функция непрерывна в каждой изолированной точке своей области определения.
-
Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция f непрерывна в точке x0, предельной для множества E, если f имеет предел в точке x0, и этот предел совпадает со значением функции f(x0).
-
Функция непрерывна в точке, если её колебание в данной точке равно нулю.
Свойства Локальные
-
Функция, непрерывная в точке
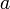 ,
является ограниченной в некоторой
окрестности этой точки.
,
является ограниченной в некоторой
окрестности этой точки. -
Если функция
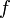 непрерывна
в точке
непрерывна
в точке
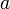 и
и
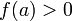 (или
(или
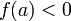 ),
то
),
то
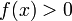 (или
(или
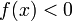 )
для всех
)
для всех
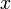 ,
достаточно близких к
,
достаточно близких к
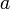 .
. -
Если функции
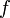 и
и
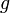 непрерывны
в точке
непрерывны
в точке
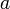 ,
то функции
,
то функции
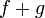 и
и
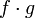 тоже
непрерывны в точке
тоже
непрерывны в точке
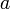 .
. -
Если функции
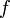 и
и
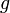 непрерывны
в точке
непрерывны
в точке
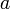 и
при этом
и
при этом
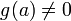 ,
то функция
,
то функция
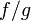 тоже
непрерывна в точке
тоже
непрерывна в точке
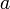 .
. -
Если функция
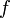 непрерывна
в точке
непрерывна
в точке
 и
функция
и
функция
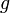 непрерывна
в точке
непрерывна
в точке
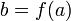 ,
то их композиция
,
то их композиция
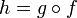 непрерывна
в точке
непрерывна
в точке
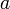 .
.
Глобальные
-
Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
-
Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
-
Областью значений функции
 ,
непрерывной на отрезке
,
непрерывной на отрезке
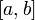 ,
является отрезок
,
является отрезок
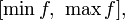 где
минимум и максимум берутся по отрезку
где
минимум и максимум берутся по отрезку
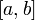 .
. -
Если функция
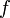 непрерывна
на отрезке
непрерывна
на отрезке
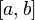 и
и
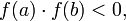 то
существует точка
то
существует точка
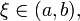 в
которой
в
которой
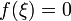 .
. -
Если функция
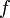 непрерывна
на отрезке
непрерывна
на отрезке
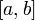 и
число
и
число
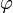 удовлетворяет
неравенству
удовлетворяет
неравенству
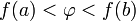 или
неравенству
или
неравенству
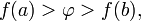 то
существует точка
то
существует точка
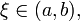 в
которой
в
которой
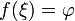 .
. -
Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
-
Монотонная функция на отрезке
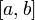 непрерывна
в том и только в том случае, когда область
ее значений является отрезком с концами
непрерывна
в том и только в том случае, когда область
ее значений является отрезком с концами
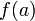 и
и
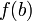 .
. -
Если функции
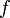 и
и
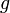 непрерывны
на отрезке
непрерывны
на отрезке
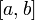 ,
причем
,
причем
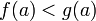 и
и
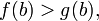 то
существует точка
то
существует точка
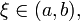 в
которой
в
которой
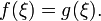 Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
