43. Физические приложения определенного интеграла (работа переменной силы при прямолинейном перемещении материальной точки, давление жидкости на пла­стинку).

Работа переменной силы

Пусть материальная точка М перемещается вдоль оси Ох под действием переменной силы F = F(x), направленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положения х = а в положение х = b (a < b), находится по формуле (см. п. 36).

Давление жидкости на вертикальную пластинку

По закону Паскаля давление жидкости на горизонтальную пластину равно весу столба этой жидкости, имеющего основанием пластинку, а высотой — глубину ее погружения от свободной поверхности жидкости, т. е. Р = gSh, где g — ускорение свободного падения,  — плотность жидкости, S - площадь пластинки, h - глубина ее погружения.

По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах.

Пусть в жидкость погружена вертикально пластина, ограниченная линиями х = а, х = b, у₁ = f₁(x) и у₂=ƒ₂(х); система координат выбрана так, как указано на рисунке 194. Для нахождения давления Р жидкости на эту пластину применим схему II (метод дифференциала).

1. Пусть часть искомой величины Р есть функция от х: р=р(х), т. е. р=р(х) — давление на часть пластины, соответствующее отрезку [а; х] значений переменной х, где х є [а; b] (р(а)=0,р(b) = Р).

2. Дадим аргументу х приращение Δх = dx. Функция р(х) получит приращение Δр (на рисунке — полоска-слой толщины dx). Найдем дифференциал dp этой функции. Ввиду малости dx будем приближенно считать полоску прямоугольником, все точки которого находятся на одной  глубине х, т. е. пластинка эта — горизонтальная.

Тогда по закону Паскаля

3. Интегрируя полученное равенство в пределах от х = а до х = В, получим

 

V. Функции многих переменных.

44. Функции многих переменных (фмп). Область определения, предел в точке, не­прерывность

Пусть дано множество , и пусть указано правило, по которому каждой точке соответствует некоторое число . В этом случае говорят, что задана функция с областью определения и областью значений . При этом и называют независимыми переменными (аргументами), а – зависимой переменной (функцией).

 

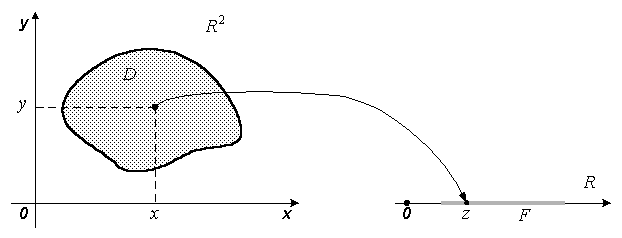
Функцию часто записывают в виде «». Схематично функция может быть изображена так, как это показано на рис. 1.

Рис.1.

Пример. На множестве определим функцию ; тогда ее областью значений является отрезок . Эту функцию можно определить, конечно, и на всей плоскости ; в этом случае имеем и .

Графиком функции называют множество точек ; обычно графиком является некоторая поверхность (рис. 2).

При построении графика функции часто пользуются методом сечений.

Пример. Построить график функции и найти . Рис.2.

Воспользуемся методом сечений.

– в плоскости – парабола.

– в плоскости –парабола.

– в плоскости – окружность.

Искомая поверхность – параболоид вращения (рис. 3). ^ Рис.3.

Расстоянием между двумя произвольными точками и (евклидова) пространства называется число

.

Множество точек называется открытым кругом радиуса с центром в точке , – окружностью радиуса с центром в точке .

Открытый круг радиуса с центром в точке называется -окрестностью точки .

Определение. Точка называется внутренней точкой множества , если существует -окрестность точки , целиком принадлежащая множеству (т.е. ) (рис. 4).

Определение. Точка называется граничной точкой множества , если в любой ее -окрестности содержатся точки, как принадлежащие множеству , так и не принадлежащие ему (рис. 5). Рис.4.

Граничная точка множества может как принадлежать этому множеству, так и не принадлежать ему.

Определение. Множество называется откры-тым, если все его точки – внутренние.

Определение. Множество называется замк-нутым, если оно содержит все свои граничные точки. Множество всех граничных точек множества называется его границей (и часто обозначается символом ). Заметим, что множество является замкнутым и называется замыканием множества . Рис.5.

Пример. Если , то . При этом . Покажите это!

Определение. Точка называется предельной точкой множества , если в любой -окрестности точки содержатся точки множества , отличные от .

Образно говоря, точка называется предельной точкой множества , если «к точке можно подойти сколь угодно близко, идя по точкам множества и не наступая на саму точку ». Предельная точка множества может принадлежать, а может не принадлежать этому множеству.

Пример. Множество совпадает с множеством своих предельных точек. Множество имеет единственную предельную точку . Покажите это!