35. Интегрирование тригонометрических функций. Универсальная подстановка. Не­которые частные случаи

1.4 Интегрирование тригонометрических функций.

1. Интегралы вида , где рациональная функция от u и v.

Интегралы указанного вида сводятся к интегралам от рациональной функции новой переменной t с помощью подстановки , которую называют универсальной тригонометрической подстановкой. При этом используются формулы тригонометрии 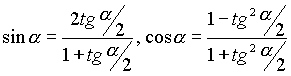. Смотри пример 1 .

Замечание. Универсальная тригонометрическая подстановка часто приводит к громоздким вычислениям. Поэтому чаще применяются другие подстановки.

2. Подынтегральная функция удовлетворяет условию

(1)

или условию

. (2)

Тогда можно использовать подстановку , или , соответственно. Смотри пример 2 .

3. Подынтегральная функция удовлетворяет условию . Это условие выполняется в частности для функций, содержащих только четные степени и В этом случае часто применяют замену переменной , где или , где .При этом, так как или ,то . Функции и выражаются через t с помощью тригонометрических формул и . Смотри пример 3 .

4. Вычисление интегралов вида , где m и n ? целые числа.

В этом случае полезно пользоваться следующими правилами:

А) если m - нечетное положительное число, то вносим под знак дифференциала или, (что то же самое) делаем замену переменной . При этом число n может быть рациональной дробью. Аналогично, если n - нечетное положительное число, то вносим под знак дифференциала или применяем подстановку .

37.Интегралы, содержащие квадратичную иррациональность, и их вычисление с по­мощью тригонометрических подстановок

Рассмотрим некоторые типы интегралов, содержащих иррациональные функции.

Интегралы типа называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим обpaзoм: под радикалом выделить полный квадрат

и сделать подстановку х +b/2a=t. При этом первые два интеграла приводятся к табличным, а третий - к сумме двух табличных интегралов.

Пример 33.1. Найти интегралы

Решение: Так как,

то

Cдeлаем подстановку x+1/4=t, x=t-1/4,dx=dt. Тогда

• 33.3. Тригонометрическая подстановка

Интегралы типа приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью следующих тригонометрических подстановок: х=а•sint для первого интеграла; х=а•tgt для второго интеграла; для третьего интеграла.

IV. Определенный интеграл.

38. Понятие определенного интеграла, его геометрический смысл, свойства

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.

Пусть f(x) определена на [a;b]. Разобьём [a;b]на части с несколькими произвольными точками a = x₀ < x₁ < x₂ < x_n = b Тогда говорят, что произведено разбиение RR отрезка [a;b] Далее выберем произв. точку , i = 0, Определённым интегралом от функции f(x) на отрезке [a;b]называется предел интегральных сумм Θ_R при , если он существует независимо от разбиения R и выбора точек ξ_i, т.е. (1) Если существует (1), то функция f(x) называется интегрируемой на [a;b] – определение интеграла по Риману.

• 

• a – нижний предел.

• b – верхний предел.

• f(x) – подынтегральная функция.

• λ_R - длина частичного отрезка.

• σ_R – интегральная сумма от функции f(x) на [a;b] соответствующей разбиению R.

• λ_R - максимальная длина част. отрезка.

Определение интеграла на языке ε, δ: Число I – называется определённым интегралом от f(x) на [ a ; b ], если для любого ε>0 существует δ=δ(ε)>0: для любого разбиения R отрезка [ a ; b ]: λ_R < δ, выполняется неравенство: |I- σ_R | = |∑^n-1_i=0f(ξi) Δxi - I| < ε при любом ξi є [ xi ; xi+1] Тогда I = ∫_a^bf(x)dx

Геометрический смысл

Определённый интеграл как площадь фигуры

Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).