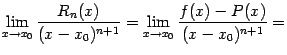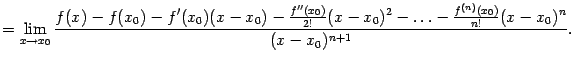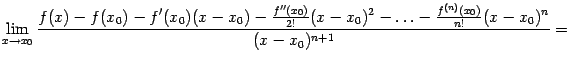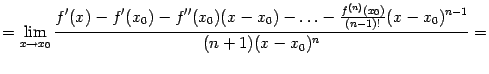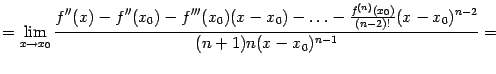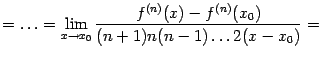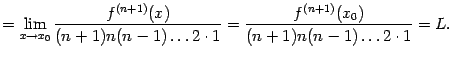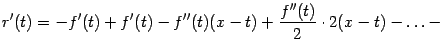- •I. Введение в анализ.
- •Предел функции в точке и на бесконечности. Геометрическая интерпретация. Теорема о единственности предела.
- •Бесконечно малые и бесконечно большие функции, их свойства
- •Теорема о связи функции с её пределом в точке
- •Алгебраические свойства пределов
- •Первый замечательный предел
- •Понятие предела последовательности. Теорема существования предела последовательности
- •Сравнение функций.
- •8. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции. Таблица эквивалентности
- •9. Понятие непрерывной функции в точке. Свойства непрерывных в точке функций
- •Свойства Локальные
- •Глобальные
- •10.Односторонние пределы функции в точке. Точки разрыва и их классификация.
- •Односторонний предел по Гейне
- •11.Основные теоремы о непрерывных на отрезке функциях
- •11. Дифференциальное исчисление функций одной перемен-
- •Правила дифференцирования функций
- •Производная сложной, обратной, параметрически заданной функции
- •Понятие дифференциала функции и его геометрический смысл. Применение дифференциала к приближенным вычислениям
- •Основные теоремы о дифференцируемых функциях (т.Ролля, Лагранжа, Коши)
- •Производные и дифференциалы высших порядков
- •Правило Лопиталя раскрытия неопределенностей. Раскрытие показательных неопределенностей
- •Формула Тейлора с остаточным членом в форме Лагранжа и Пеано
- •Разложение основных функций по формуле Тейлора
- •Монотонные функции. Признаки возрастания (убывания) функции на интервале
- •Понятие экстремума функции в точке. Необходимое и достаточное условия экс тремума функции в точке
- •Исследование функций на экстремум с помощью высших производных
- •Наибольшее и наименьшее значения функции на отрезке
- •Выпуклость и вогнутость графика функции, точка перегиба. Необходимое и достаточное условия точки перегиба графика функции
- •Понятие асимптоты графика функции. Нахождение вертикальных и наклонных асимптот
- •Полное исследование функции и построение графика функции
- •III. Неопределенный интеграл.
- •Понятие первообразной и ее свойства. Теорема о множестве первообразных
- •30.Таблица неопределенных интегралов основных функций
- •Интегрирование по частям и заменой переменной в неопределенном интеграле
- •Интегрирование функций с квадратным трехчленом в знаменателе
- •Интегрирование рациональных дробей методом разложения на простые дроби
- •Рекуррентные формулы. Вычисление интеграла
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций. Универсальная подстановка. Некоторые частные случаи
- •1.4 Интегрирование тригонометрических функций.
- •37.Интегралы, содержащие квадратичную иррациональность, и их вычисление с помощью тригонометрических подстановок
- •IV. Определенный интеграл.
- •Понятие определенного интеграла, его геометрический смысл, свойства
- •Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница
- •Интегрирование по частям и заменой переменной в определенном интеграле
- •Для неопределённого интеграла
- •Для определённого
- •Несобственные интегралы I и п рода. Определение, свойства, теоремы сравнения
- •Несобственные интегралы I рода
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •Несобственные интегралы II рода
- •Геометрический смысл несобственных интегралов II рода
- •Геометрические приложения определенного интеграла:
- •43. Физические приложения определенного интеграла (работа переменной силы при прямолинейном перемещении материальной точки, давление жидкости на пластинку).
- •V. Функции многих переменных.
- •44. Функции многих переменных (фмп). Область определения, предел в точке, непрерывность
- •2. Предел функции.
- •Понятие частной производной фмп. Правила дифференцирования
- •Дифференцирование сложной функции многих переменных. Формула для производной неявно заданной функции одной переменной
- •Касательная плоскость и нормаль к поверхности
- •Частный и полный дифференциалы фмп. Применение дифференциала к приближенным вычислениям
- •Частные производные высших порядков. Теорема о равенстве смешанных производных
- •Дифференциалы высших порядков
- •Формула Тейлора для функции двух переменных
- •Различные формы остаточного члена
- •Экстремумы фмп. Необходимое и достаточное условия экстремума фмп в точке
- •Постановка задач на экстремум. Нахождение наибольшего и наименьшего значений функции в замкнутой области
-
Формула Тейлора с остаточным членом в форме Лагранжа и Пеано
Теорема
6.1 (формула
Тейлора с остаточным членом в форме
Пеано) Пусть
![]() --
остаток в формуле Тейлора для функции
--
остаток в формуле Тейлора для функции
![]() в
точке
в
точке
![]() ,
и функция
,
и функция
![]() имеет
непрерывную
имеет
непрерывную
![]() -ю
производную. Тогда
-ю
производную. Тогда
![]() --
бесконечно малая величина того же или
большего порядка малости, как
--
бесконечно малая величина того же или
большего порядка малости, как
![]() ,
при
,
при
![]() .
(Остаточный член
.
(Остаточный член
![]() ,
о котором известны эти сведения о порядке
малости, называется остаточным
членом в форме Пеано.)
,
о котором известны эти сведения о порядке
малости, называется остаточным
членом в форме Пеано.)
Доказательство. Утверждение теоремы означает, что существует
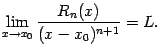
При
![]() остаток
остаток
![]() будет
иметь тот же порядок малости, что
будет
иметь тот же порядок малости, что
![]() ,
а при
,
а при
![]() --
больший порядок малости. Итак, вычислим
предел:
--
больший порядок малости. Итак, вычислим
предел:
|
|
|
|
|
|
Применим
к этому пределу правило Лопиталя,
повторив этот приём
![]() раз:
раз:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последний
предел мы вычислили прямой подстановкой,
поскольку по предположению
![]() --
непрерывная функция. Существование
предела доказывает утверждение теоремы.
--
непрерывная функция. Существование
предела доказывает утверждение теоремы.
Доказанная
теорема утверждает, что при малых
отклонениях от
![]() значения
значения
![]() будут
отклоняться от
будут
отклоняться от
![]() не
более чем на величину
не
более чем на величину
![]() -го
порядка малости относительно разности
-го
порядка малости относительно разности
![]() ,
что даёт нам уверенность в том, что
замена
,
что даёт нам уверенность в том, что
замена
![]() на
многочлен Тейлора
на
многочлен Тейлора
![]() будет
давать очень хорошее приближение, и это
приближение будет улучшаться, если мы
будем увеличивать значения
будет
давать очень хорошее приближение, и это
приближение будет улучшаться, если мы
будем увеличивать значения
![]() .
Однако доказанная теорема не даёт нам
оценки остатка
.
Однако доказанная теорема не даёт нам
оценки остатка
![]() .
Этот пробел устраняет следующая теорема.
.
Этот пробел устраняет следующая теорема.
Теорема
6.2 (остаток
в формуле Тейлора в форме Лагранжа)
Пусть при
всех
![]() существует
существует
![]() -я
производная
-я
производная
![]() .
Тогда для любого
.
Тогда для любого
![]() существует
точка
существует
точка
![]() ,
лежащая между
,
лежащая между
![]() и
и
![]() (то
есть
(то
есть
![]() при
при
![]() ),
такая что
),
такая что
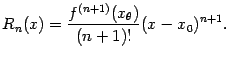
(Остаточный член формулы Тейлора, представленный в таком виде, называется остаточным членом в форме Лагранжа.)
Доказательство.
Это доказательство не столь прямолинейное,
как в предыдущей теореме. Рассмотрим
вспомогательную функцию
![]() переменного
переменного
![]() ,
изменяющегося в рассматриваемой
окрестности
,
изменяющегося в рассматриваемой
окрестности
![]() точки
точки
![]() .
Эта функция будет зависеть также от
параметра
.
Эта функция будет зависеть также от
параметра
![]() :
:
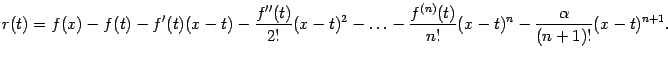
Подберём
такое значение параметра
![]() ,
равное
,
равное
![]() ,
чтобы при
,
чтобы при
![]() функция
обращалась в 0:
функция
обращалась в 0:
![]() .
Фиксируем такое значение
.
Фиксируем такое значение
![]() .
.
Тогда
функция
![]() удовлетворяет
условиям теоремы Ролля на отрезке
удовлетворяет
условиям теоремы Ролля на отрезке
![]() (или
(или
![]() ,
если
,
если
![]() ):
):
![]() ,
что очевидно по определению функции
,
что очевидно по определению функции
![]() ;
;
![]() согласно
выбору параметра; дифференцируемость
на
согласно
выбору параметра; дифференцируемость
на
![]() и
непрерывность в точках
и
непрерывность в точках
![]() и
и
![]() следуют
из предположенных свойств функции
следуют
из предположенных свойств функции
![]() .
По теореме Ролля существует такая точка
.
По теореме Ролля существует такая точка
![]() ,
что
,
что
![]()
Однако
нетрудно подсчитать, находя производные
произведений в определении функции
![]() ,
что
,
что
|
|
|
|
|
|
Все слагаемые в начале правой части, включая обозначенные многоточием, взаимно уничтожаются, так что получаем
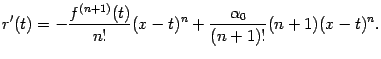
Подстановка
![]() даёт
даёт
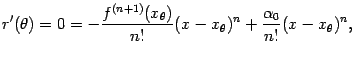
откуда следует, что
![]()
Теперь
вспомним, что значение параметра мы
выбрали так, что
![]() .
Подставив найденное значение
.
Подставив найденное значение
![]() в
выражение для
в
выражение для
![]() ,
получим:
,
получим:
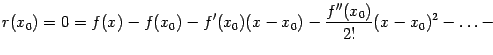
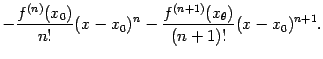
Отсюда получаем, наконец,
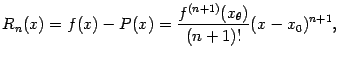 что
и требовалось доказать.
что
и требовалось доказать.