Упражнения

1. Задать несколько типов для функции f(x):

а) f (x)= ; г) f(x)=cosx;

б) f(x)=x² ; д) f(x)=2^x;

в) f(x)=2x – 4; е) f(x)=lgx.

Для каждого из заданных типов функции f определить:

1) свойства f;

2) является ли отображением, если да, то каким;

3) имеет ли обратную функцию f ^-1?

2. Найти композицию функций f(x) и g(x)

а) f(x)=2х и g(x)=lgx;

б)f(x)=х³ и g(x)=;

в)f(x)=2^х и g(x)=x+1.

3. Функции f и g имеют тип:

а) f: A^2→B и g: B⁵→C;

б)f: A⁴ →B и g: B³ →C.

Найти несколько композиций функций f · g и определить их тип.

4. Найти композиции преобразований:

а) ;

б) ;

в) .

Глава 6 Графы Теория графов. Основные понятия

Графом g называется совокупность двух множеств: вершин V и ребер Е, между элементами которых определенно отношение инцидентности – каждое ребро еЕ инцидентно двум вершинам ν΄ и ν˝V, которые оно соединяет. При этом вершины ν΄, ν˝ и ребро е называются инцидентными друг другу, а вершины ν΄ и ν˝, являющиеся для ребра е концевыми точками, называются смежными.

Ребро, соединяющее две вершины, может иметь направление от одной вершины к другой: в этом случае оно называется направленным или ориентированным.

Граф, содержащий направленные ребра (дуги) с началом ν΄ и концом ν˝ называется ориентированным (орграфом), а ненаправленный – неориентированным (н-графом).

Локальной степенью вершины νV н-графа g называется количество ребер ρ(ν), инцидентных вершине ν. В н-графе сумма степеней всех вершин равна удвоенному числу ребер m графа (петля дает вклад 2 в степень вершины):

Для вершин орграфа определяются две локальные степени:

- ρ₁(ν) – число ребер с началом в вершине ν, или количество выходящих из ν ребер;

- ρ₂(ν) – количество входящих в ν ребер, для которых эта вершина является концом.

Петля дает вклад 1 в обе эти степени.

, где m – количество ребер для орграфа.

Способы задания графов

1. Графический.

2. В виде множеств вершин V и ребер Е, когда каждое ребро еЕ, определенно парой инцидентных ему концевых вершин (ν΄ и ν˝).

3. Матрицей инцидентности Еij размера m x n: по вертикали и горизонтали указываются вершины и ребра соответственно, а на пересечении i-ой вершины и j-ого ребра в случае н-графа проставляется 1, если они инцидентны, и 0 – в противном случае:

Для орграфа:

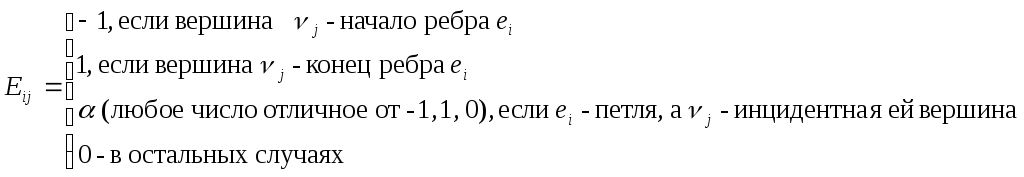
4. Списком ребер графа, представленным двумя столбцами: в левом перечисляются все ребра еi Е, а в правом – инцидентные ему вершины νj΄, νj˝, для н-графа порядок вершин в строке произволен, для орграфа первым стоит номер начала ребра.

5. Матрицей смежности δij – квадратной матрицей размера n x n: по вертикали и горизонтали перечисляются все вершины νjV, а на пересечении к-ой и i-ой вершин в случае н-графа проставляется число, равное числу рёбер, соединяющих эти вершины.

Для орграфа проставляется число, равное числу рёбер с началом к-ой вершине и концом в i-ой.

- Графы G₁ и G₂ равны, т.е. G₁ = G₂, если их множества вершин и ребер, выраженных через пары инцидентных им вершин, совпадают: V₁ = V₂, E₁ = E₂.

Пример:

G

₁: G₂:

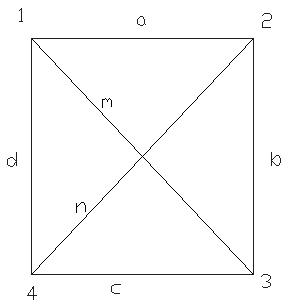
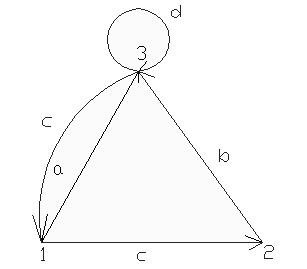
Рис. 6.1

Рис. 6.2

G

₃: G₄:

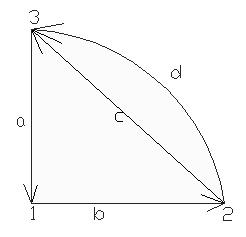
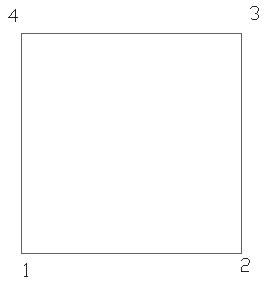
Рис. 6.3

Рис. 6.4

G₅:

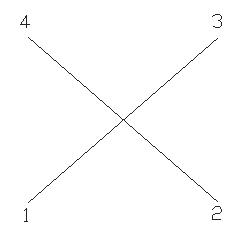
Рис. 6.5

G₁, G₄, G₅ (рис. 6.1, 6.4, 6.5)– н-граф, G₂, G₃ (рис. 6.2, 6.3)– орграф

В G₂ ребро d – петля, ребро k– дуга (рис. 6.2).

В G₃ ребра c и d исходят из одних и тех же вершин и одинаково ориентированные. Такие ребра называют кратными, а граф – мультиграфом (рис. 6.3).

G₄ и G₅ являются дополнением друг другу (рис. 6.4, 6.5).

Пример:

З

адать матрицами инцидентности, смежности, а также списком рёбер графы G₁ (рис. 6.6) и G₂ (рис. 6.7):

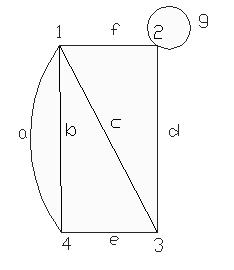
G₁:

Рис. 6.6

Для G₁:

Матрица инцидентности:

Eij	a	b	c	d	e	f	g
1	1	1	1	0	0	1	0
2	0	0	0	1	0	1	1
3	0	0	1	1	1	0	0
4	1	1	0	0	1	0	0

Матрица смежности:

		δ			1	2		3	4
		1			0	1		1	2
		2			1	1		1	0
		3			1	1		0	1
		4			2	0		1	0

A	(1,4)
B	(1,4)
C	(1,3)
D	(2,3)
E	(4,3)
F	(1,2)
G	(2,2)

Матрица смежности для н-графа всегда симметрична относительно главной диагонали.

G

₂:

Рис. 6.7

Для G₂:

Матрица инцидентности:

Eij	a	b	c	d	e	f	g	k
1	1	-1	0	0	0	1	0	0
2	0	0	1	0	0	-1	-1	0
3	0	0	0	-1	-1	0	1	2
4	-1	1	-1	1	1	0	0	0

Матрица смежности:

		δ			1	2		3	4
		1			0	0		0	1
		2			1	0		1	0
		3			0	0		1	2
		4			1	1		0	0

A	(4,1)
B	(1,4)
C	(4,2)
D	(3,4)
E	(3,4)
F	(2,1)
G	(2,3)
K	(3,3)

Пример:

Ч

ему равны локальные степени вершин графов G3 (рис. 6.8) и G4 (рис. 6.9)?

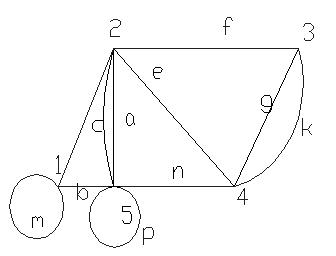
G₃:

Рис. 6.8

Для G₃:

ρ(1) = 4, ρ(2) = 5, ρ(3) = 3, ρ(4) = 4, ρ(5) = 6

m – число ребер графа G3.

G

₄:

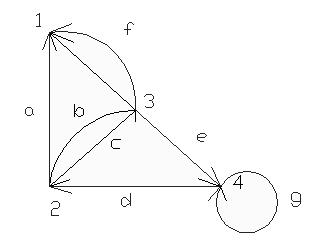
Рис. 6.9

Для G₄:

ρ₁(1) = 0, ρ₁(2) = 2, ρ₁(3) = 4, ρ₁(4) = 2

ρ₂(1) = 3, ρ₂(2) = 2, ρ₂(3) = 1, ρ₂(4) = 2

m – число ребер графа G₄.