Решение

1) Пусть испытание S: из каждой коробки наудачу вынимают по одной паре обуви.

Обозначим события, вероятности которых следует найти:

Е₁  только одна пара обуви первого сорта;

Е₂  обе пары обуви первого сорта;

Е₃  хотя бы одна пара обуви первого сорта.

Введем вспомогательные события:

А  из первой коробки извлечена пара обуви первого сорта;

В  из второй коробки извлечена пара обуви первого сорта.

Тогда

 из первой коробки извлечена пара обуви второго сорта;

 из второй коробки извлечена пара обуви второго сорта.

События Е₁, Е₂, Е₃ являются сложными и выражаются через события А, В, , следующим образом:

Е₁ = +, т.е. либо только из первой коробки извлечена пара обуви первого сорта, либо только из второй;

Е₂=АВ, т.е. из обеих коробок извлечено по паре обуви первого сорта;

Е₃=А + В.

События А и В являются совместными, т.к. из каждой коробки может быть извлечено по паре обуви первого сорта.

События А и В независимы, т.к. вероятность извлечения из второй коробки пары обуви первого сорта не зависит от того, какого сорта пара обуви была извлечена из первой коробки, т.е Р_А(В)= Р_Ā(В).

Также независимыми являются пары событий А и и В.

Вычислим вероятности исходных событий А и В:

т.к. в первой коробке 10 пар обуви, из них 4 пары первого сорта.

т.к. во второй коробке 15 пар обуви, из них 12 пар первого сорта.

Вычислим вероятности противоположных событий:

и

Перейдем к вычислению вероятностей событий Е₁, Е₂, Е₃.

1. Е₁ = +.

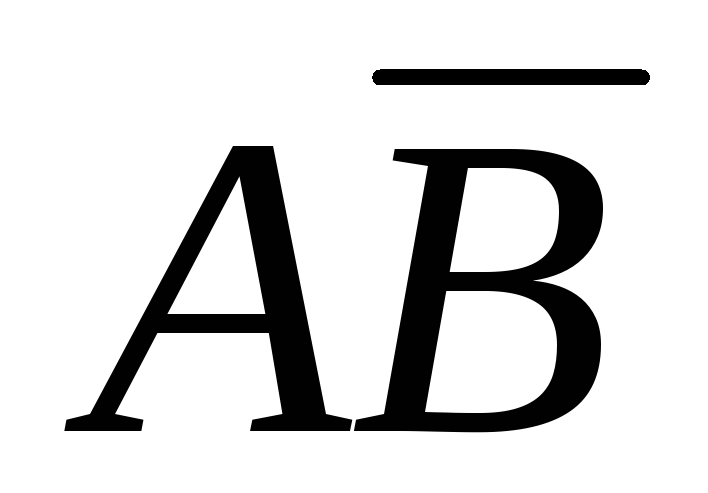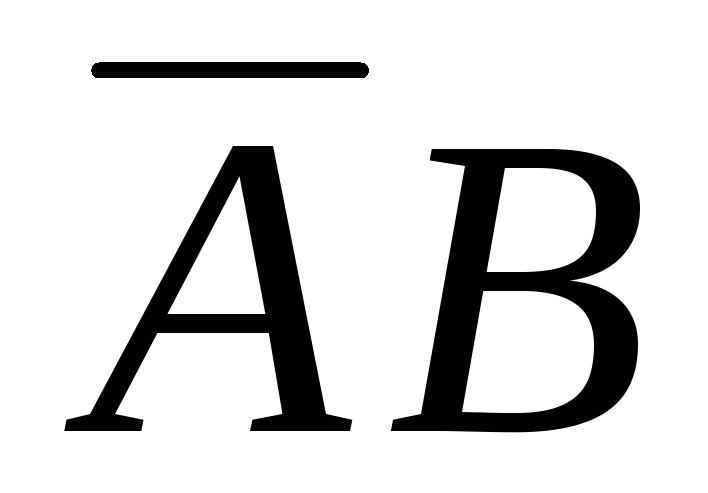События и несовместны. По теореме сложения вероятностей для несовместных событий получим:

где и  произведения независимых событий.

По теореме умножения вероятностей для независимых событий

Окончательно:

б) Е₂=АВ.

По теореме умножения вероятностей для независимых событий получим:

в) Е₃=А + В.

События А и В совместны. По теореме сложения вероятностей для совместных событий получим:

Р(Е₃) = Р(А + В) = Р(А) + Р(В)  Р(АВ) = 0,4 + 0,8  0,32 = 0,88.

Вероятность события Е₃ можно вычислить иначе.

Так как Е₃=Е₁+Е₂, причем события Е₁ и Е₂ несовместны, то используя предыдущие результаты, получим:

Р(Е₃) = Р(Е₁ + Е₂) = Р(Е₁) + Р(Е₂) = 0,56 + 0,32 = 0,88.

2) Пусть испытание S: из коробки наудачу одну за другой вынимают две пары обуви.

Е₁  только одна пара обуви первого сорта;

Е₂  обе пары обуви первого сорта;

Е₃  хотя бы одна пара обуви первого сорта.

Введем вспомогательные события:

А  первая извлеченная пара обуви оказалась первого сорта;

В  вторая извлеченная пара обуви оказалась первого сорта.

Тогда

 первая извлеченная пара обуви оказалась второго сорта;

 вторая извлеченная пара обуви оказалась второго сорта.

События Е₁, Е₂, Е₃ выражаются через события А, В, , следующим образом:

Е₁ = +, т.е. либо только первая пара обуви оказалась первого сорта, либо только вторая;

Е₂=АВ, т.е. обе пары обуви оказались первого сорта;

Е₃ = Е₁ + Е₂.

События А и В совместны, т.к. обе извлеченные пары обуви могут оказаться первого сорта.

Проверим, являются события A и B зависимыми или независимыми.

 вероятность во второй раз извлечь пару обуви первого сорта при условии, что в первый раз была извлечена пара обуви также первого сорта.

 вероятность во второй раз извлечь пару обуви первого сорта при условии, что в первый раз была извлечена пара обуви второго сорта.

, следовательно, A и B  зависимые события.

Вычислим вероятности вспомогательных событий:

т.к. в коробке всего 25 пар обуви, из них 16 пар первого сорта.

Вероятность Р(В) непосредственно вычислить невозможно, т.к. к моменту извлечения второй пары обуви в коробке останется 24 пары, а первосортных среди них либо 15 пар, либо 16 пар, в зависимости от того, какого сорта извлечена первая пара обуви.

Перейдем к вычислению вероятностей событий Е₁, Е₂, Е₃.

a) Е₁ = +.

Используя теорему сложения вероятностей для несовместных событий и и теорему умножения вероятностей для зависимых событий, получим

 вероятность во второй раз извлечь пару обуви второго сорта при условии, что в первый раз была извлечена пара обуви первого сорта, т.к. после первого извлечения остается 24 пары обуви, из которых 9 пар второго сорта.

вычислено ранее.

Подставляя вычисленные вероятности, получим:

б) Е₂=АВ;

По теореме умножения вероятностей для зависимых событий

P(E₂) = P(AB) = P(A)· P_A(B) =

вычислено ранее.

в) Е₃ = Е₁ + Е₂.

По теореме сложения вероятностей для несовместных событий Е₁ и Е₂, используя предыдущие результаты, получим

Р(Е₃) = Р(Е₁ +Е₂)= Р(Е₁) + Р(Е₂) = 0,48 + 0,4 = 0,88.