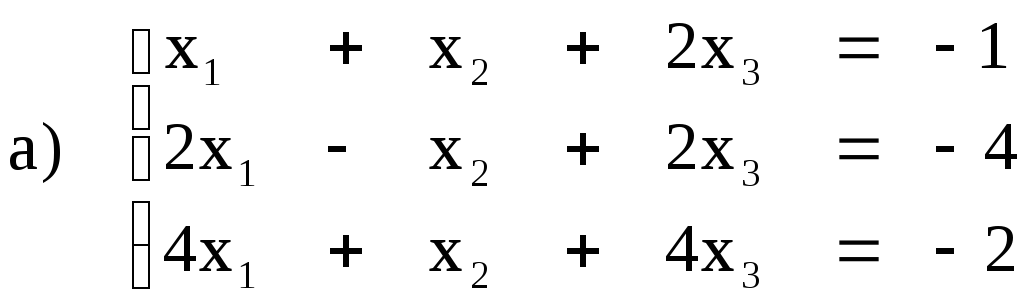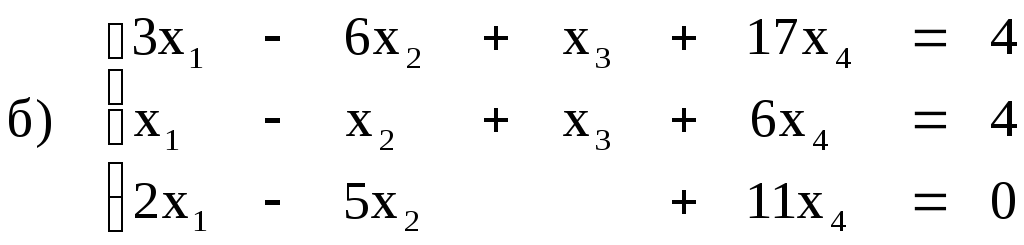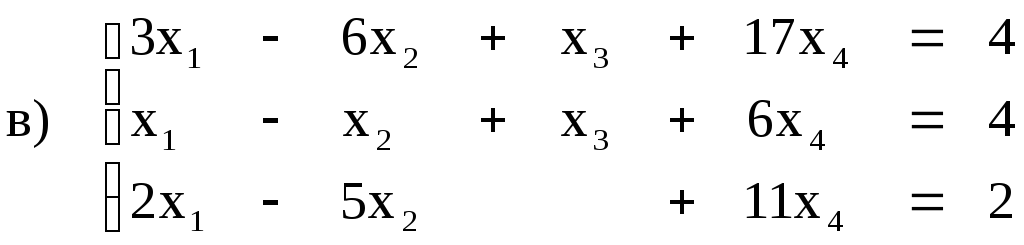Решение

1) Построим диаграмму рассеяния (см. рис. в конце решения задачи)

1. определим выборочный коэффициент корреляции r_B, для этого составим расчетную таблицу и найдем суммы по всем её столбцам.

Х	Y	X2	Y2	XY
14,5	1,2	210,25	1,44	17,4
14,8	1,22	219,04	1,4884	18,056
14	0,95	196	0,9025	13,3
15,1	1,34	228,01	1,7956	20,234
15,3	1,42	234,09	2,0164	21,726
13,5	1,1	182,25	1,21	14,85
14,9	1,22	222,01	1,4884	18,178
14,8	1,3	219,04	1,69	19,24
15	1,23	225	1,5129	18,45
14,3	1,1	204,49	1,21	15,73
Итого: 146,2	12,08	2140,18	14,7542	177,164

Используя полученные результаты, вычислим выборочные средние и выборочные стандартные отклонения признаков X и Y :

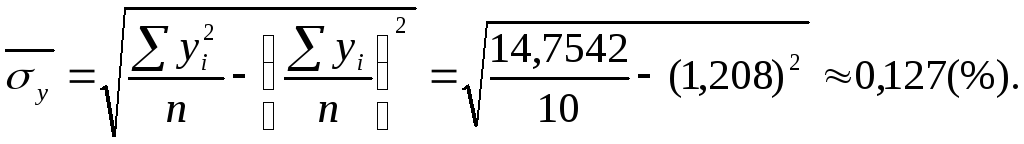
Вычислим выборочный коэффициент корреляции:

Выборочный коэффициент корреляции положителен по знаку и близок к единице. Следовательно, между признаками X и Y имеет место тесная и положительно ориентированная связь.

3) Вычислим параметры x₀, b₀, b₁ уравнения линейной регрессии:

Выборочное уравнение линейной регрессии имеет вид:

= 1,208 + 0,2015(х  14,62), или

= 0,2015х  1,738.

При х = 14,7 получим = 0,20ּ14,7  1,738 ≈1,224.

Следовательно, ожидаемое среднее значение процентного содержания органических кислот в плодах черники, когда содержание сухих веществ равно 14,7%, близко к 1,22%.

4) Построим прямую линию регрессии на том же рисунке, на котором изображена диаграмма рассеяния.

Найдем координаты двух точек этой прямой:

если х₁ = 14,7, то y₁ = 1,22;

если х₂ = 15, то у₂ = 1,28.

Диаграмма рассеяния и прямая регрессии:

Задания 141  150. Системы линейных уравнений Краткие теоретические сведения

• Общий вид системы m линейных уравнений c n неизвестными:

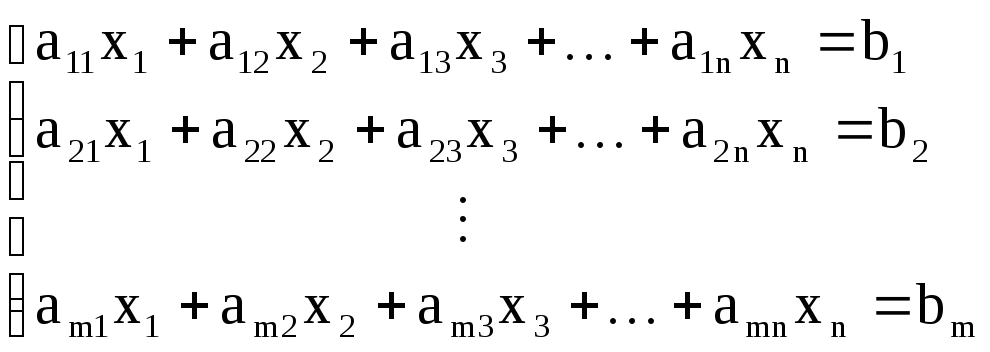
x₁, x₂, …, x_n  неизвестные;

а_ij  коэффициент i-го уравнения при неизвестной x_j при

i = 1, 2, 3 …, m, j = 1, 2, 3 …, n;

b₁, b₂, …, b_m  свободные члены.

• Решением системы уравнений называется упорядоченный набор чисел 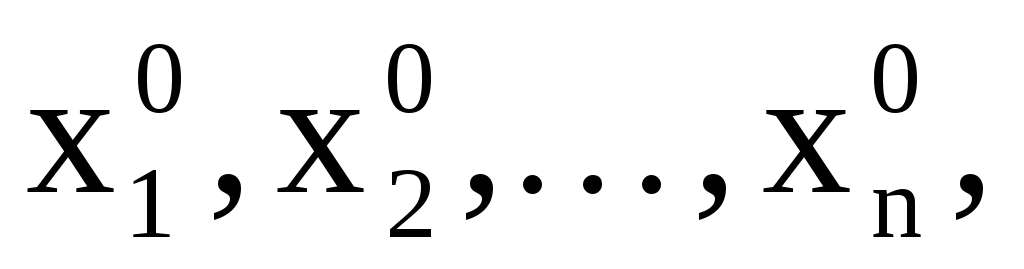который при подстановке этих чисел вместо соответствующих неизвестных обращает каждое уравнение в числовое равенство.

• Система уравнений называется совместной, если она имеет хотя бы одно решение. Система уравнений называется несовместной, если она не имеет ни одного решения.

Совместная система уравнений называется определенной, если она имеет единственное решение. Совместная система уравнений называется неопределенной, если она имеет множество решений.

Каждое решение неопределенной системы уравнений называется её частным решением.

Общее решение  это формула, по которой можно найти все частные решения системы уравнений.

• Равносильные системы уравнений  это системы, имеющие одинаковые множества решений.

• Метод Жордана-Гаусса иначе называется методом полного исключения неизвестных. Метод заключается в следующем:

Неизвестные последовательно одна за другой исключается из всех уравнений, кроме одного, в котором коэффициент при исключаемой неизвестной оказывается равным единице. В итоге преобразований получается следующая система уравнений, равносильная исходной:

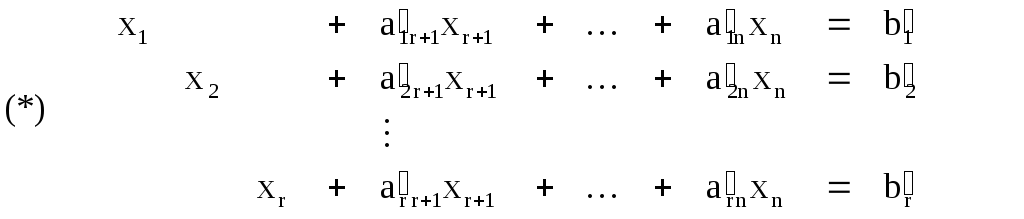
Коэффициенты системы, полученные в результате преобразований, помечены знаком ( )  штрих.

x₁, x₂, …, x_r называются базисными переменными. Каждая базисная переменная входит только в одно уравнение с коэффициентом, равным единице.

x_r+1, x_r+2, …, x_n называются свободными переменными.

Выразив базисные переменные через свободные, получим общее решение системы:

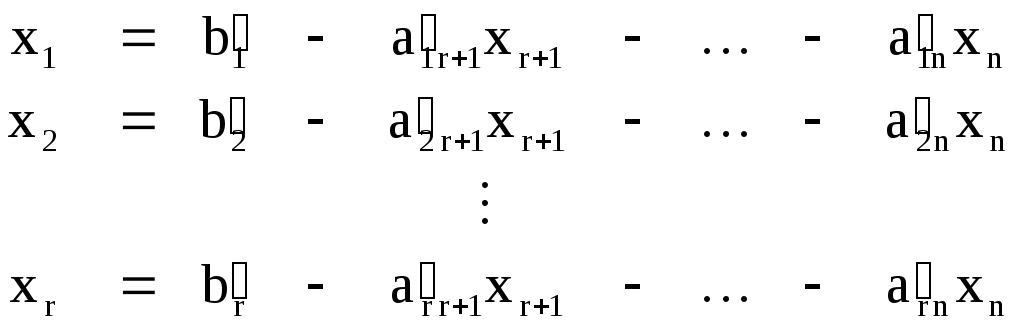
Придавая свободным переменным произвольные значения, вычислим соответствующие значения базисных переменных. Так могут быть получены различные частные решения системы.

Ясно, что r ≤ m и r ≤ n.

Если r < m, то некоторые уравнения оказались следствием остальных и исключены из рассмотрения.

Если r = n, то система не имеет свободных переменных, её решение единственно и имеет вид:

…,

Следует отметить, что только для определенности в качестве базисных выбраны переменные x₁, x₂, …, x_r, но могут быть и другие.

• Частное решение называется базисным, если значения всех свободных переменных равны нулю.

• Базисное решение называется допустимым, если значения базисных переменных неотрицательны.

• Базисное решение называется невырожденным, если значения базисных переменных отличны от нуля. В противном случае базисное решение называется вырожденным.

• Решение систем линейных уравнений удобно оформлять в виде таблиц Гаусса. Исходная таблица имеет вид:

x1	х2	…	xn	B	Контроль
a11 a21  аm1	a12 a22  аm2	… …  …	a1n a2n  аmn	b1 b2  bm	

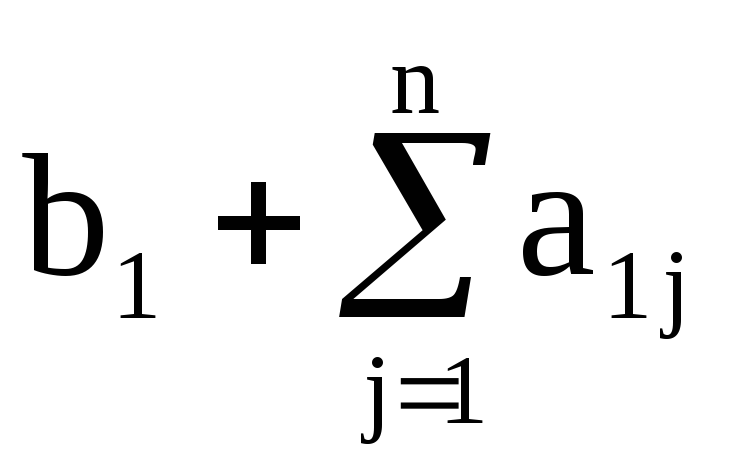
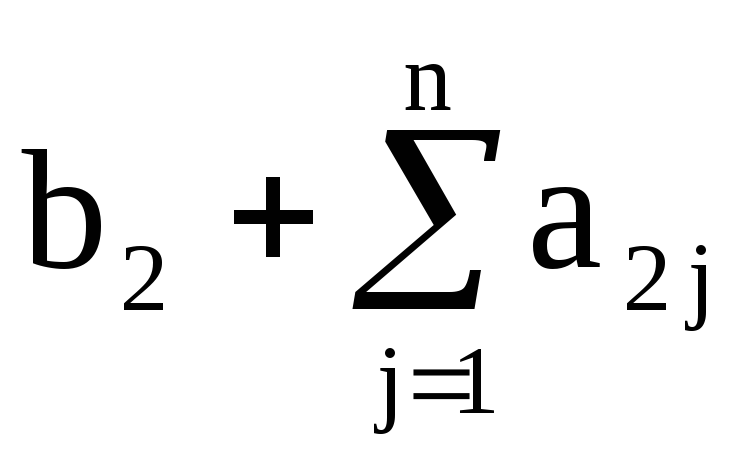
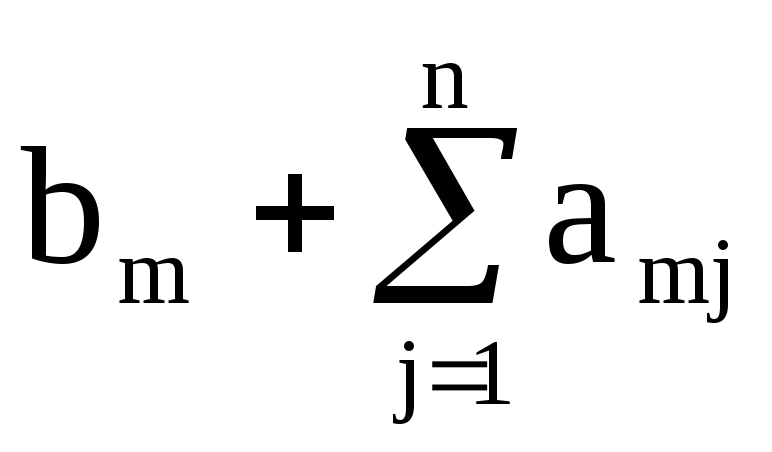
В таблицах по строкам последовательно записаны коэффициенты каждого уравнения.

В первых n столбцах записаны коэффициенты при x₁, x₂, …, x_n, в предпоследнем столбце  свободные члены системы уравнений.

Последний столбец предназначен для контроля правильности вычислений. В этом столбце записаны суммы всех предшествующих элементов соответствующих строк.

Пусть a_ij ≠ 0. Тогда переменную х_j можно исключить из всех уравнений, кроме i-го, в котором коэффициент при х_j окажется равным единице.

a_ij называют разрешающим элементом и в процессе вычислений для удобства отмечают рамкой.

Соответственно разрешающими называют i-ю строку и j-й столбец.

Иначе говоря, разрешающий элемент стоит в пересечении разрешающей строки и разрешающего столбца.

• Преобразование системы линейных уравнений по методу Жордана-Гаусса заключается в повторении следующих шагов:

1. Разрешающую строку таблицы следует разделить на разрешающий элемент;

2. В разрешающем столбце все элементы, кроме разрешающего, заменить на нули;

3. Остальные элементы таблицы, включая два последних столбца, следует пересчитать по правилу прямоугольника:

a_p … A

 

B … a_ij

a_ij  элемент, подлежащий пересчету, a_p  разрешающий элемент,

А, В  элементы таблицы Гаусса, достраивающие фигуру до воображаемого прямоугольника.

a_ij пересчитывается по следующей формуле:

• Контроль правильности вычислений:

каждый элемент контрольного столбца таблицы должен быть равен сумме всех предшествующих элементов соответствующей строки.

• Выбрав в качестве разрешающего ненулевой элемент из другой строки и другого столбца, исключим другую переменную из всех уравнений, кроме одного, и т.д. В конечном итоге система уравнений будет приведена к виду (*).

Отметим, что для упрощения вычислений в качестве разрешающего элемента удобно выбирать единицу, если это возможно.

• В процессе преобразований системы уравнений по методу Жордана-Гаусса возможны следующие ситуации:

1. В одной из строк таблицы все элементы оказываются равны нулю. В этом случае соответствующее уравнение оказывается следствием остальных и исключается из дальнейшего рассмотрения.

2. В одной из строк таблицы все элементы, кроме двух последних, равны нулю, два же последних элемента в столбцах свободных членов и контрольном отличны от нуля. В этом случае система несовместна и её решение прекращается.

• Чтобы перейти от одного базисного решения к другому, следует одну из свободных переменных перевести в базисные, а одну из базисных переменных перевести в свободные.

Пусть х_к  свободная переменная, подлежащая переводу в базисные. Если а_ik ≠ 0, то базисную переменную х_i можно перевести в свободные. Для этого нужно сделать а_ik разрешающим элементом и провести преобразования по методу Жордана-Гаусса.

Пример

Решить систему линейных уравнений методом Жордана-Гаусса. В случае неопределенности системы найти два базисных решения, выяснить, являются они допустимыми или недопустимыми, вырожденными или невырожденными и почему.