Решение

1. Данная функция определена при всех значениях аргумента х, т.е. областью её определения является вся числовая ось (; +).

2. Найдем точки пересечения графика функции с осями координат.

у(0) = (1)²(4) = 4, т.е. график пересекает ось ОУ в точке А(0;4).

у = 0, если х  1 = 0 или х  4 = 0, т.е. при х = 1 или х = 4.

В(1;0) и С(4;0)  точки пересечения графика с осью ОХ.

3. Преобразуем функцию, раскрыв скобки:

у = (х  1)²(х  4) = (х²  2х + 1)(х  4) = х³  6х² + 9х  4.

Функция является многочленом третьей степени, она непрерывна, её график  линия без разрывов.

4. Если y(x)>0 на интервале (a;b), то функция у(х) возрастает на этом интервале. Если y(x)<0 на интервале (a;b), то функция у(х) убывает на этом интервале.

Найдем производную у(х):

у(х) = (х³  6х² + 9х  4) = 3х²  12х + 9 = 3(х²  4х + 3)

у(х) = 0, если х²  4х + 3 =0.

Решая полученное квадратное уравнение, получим

х₁ = 1, х₂ = 3  его корни.

Корни производной х = 1 и х = 3 разбивают числовую ось на три интервала.

Чтобы определить знак производной в каждом интервале, вычислим её значения в некоторых точках:

у(0) = 9>0,

у(2) = 3·2²  12·2 + 9 = 3<0,

у(4) = 3·4²  12·4 + 9 = 9>0.

Следовательно, функция возрастает в интервалах (; 1) и (3; +), а в интервале (1; 3) убывает.

Исследуем функцию на экстремумы.

х = 1 и х = 3  критические точки.

х = 1  точка максимума, т.к. переходя через эту точку производная у(х) меняет свой знак с «+» на «».

х = 3  точка минимума, т.к. переходя через эту точку производная у(х) меняет свой знак с «» на «+».

у(1) = 0  максимальное значение функции,

у(3) = 3³  6·3² + 9·3  4 = 4  минимальное значение функции.

B (1;0) и D(3; 4)  точки, принадлежащие графику функции, причем точка В(1;0) была уже получена ранее.

5. Если у(х)<0 на интервале (a;b), то график функции у(х) является выпуклой кривой на этом интервале.

Если у(х)>0 на интервале (a;b), то график функции у(х) является вогнутой кривой на этом интервале.

Найдем у(х):

у(х) = (3х²  12х + 9) = 6х  12.

у(х) = 0, если 6х  12 = 0, т.е. х = 2.

Корень второй производной х = 2 разбивает числовую ось на два интервала.

+



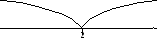
х

у(0) =  12<0,

у(3) = 6·3  12 = 6 > 0.

Следовательно, в интервале (;2) график функции является выпуклым, а в интервале (2;+)  вогнутым.

При х = 2 имеет место перегиб графика функции.

у(2) = 2³  6·2² + 9·2  4 =  2

График функции проходит через точку Е(2; 2).

6. Найдем координаты нескольких дополнительных точек для уточнения графика функции:

у(0,5) = 10,125;

у(4,5) = 6,125.

Получим дополнительные точки F(0,5; 10,125) и G(4,5; 6,125).

Для построения графика функции у = (х  1)²·(х  4) следует построить систему координат ОХУ, отметить точки А, В, С, D, E, F, G и соединить их в соответствии с проведенным исследованием.

х

y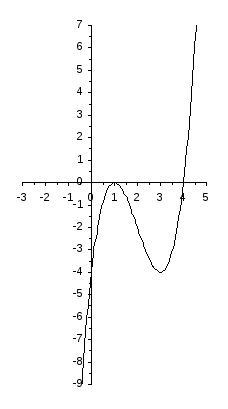

Задания 41  50. Неопределённый интеграл Краткие теоретические сведения

• Таблица неопределённых интегралов (с = const):

• Свойства неопределённых интегралов:

а) Неопределённый интеграл от суммы или разности функций равен сумме или разности интегралов от каждой функции;

б) Постоянный множитель выносится за знак неопределённого интеграла.

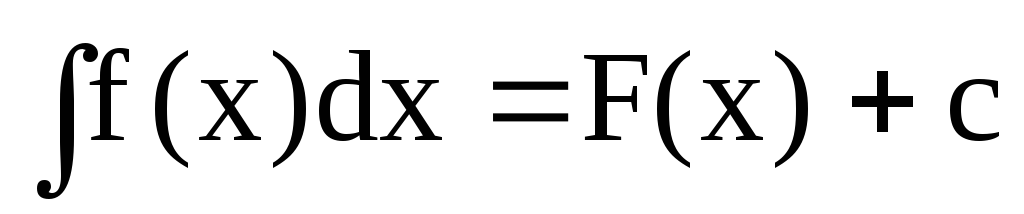
• Если  табличный интеграл, u = u(x)  дифференци-руемая функция, то

т.к.

du = u(x)dx  дифференциал функции u(x).

• При интегрировании рациональных функций, или рациональных дробей, вначале необходимо выяснить, является эта дробь правильной или неправильной.

Если степень числителя меньше степени знаменателя, то рациональная дробь является правильной.

Если степень числителя больше или равна степени знаменателя, то рациональная дробь является неправильной.

Неправильную рациональную дробь делением числителя на знаменатель следует представить в виде суммы многочлена и правильной рациональной дроби.

Правильную рациональную дробь методом неопределённых коэффициентов следует разложить в сумму простых дробей. Вид простых дробей определяется из разложения знаменателя данной рациональной дроби на множители.

• Чтобы проверить, правильно ли найден неопределённый интеграл, нужно найти производную или дифференциал от результата, при этом должна получиться подынтегральная функция или подынтегральное выражение, т.е. если

Пример

Найти неопределённые интегралы. Результаты проверить дифференцированием.

Решение

а) Найти

Представим интеграл в виде суммы интегралов, постоянные множители вынесем за знак интеграла, затем используем формулу

.

Получим:

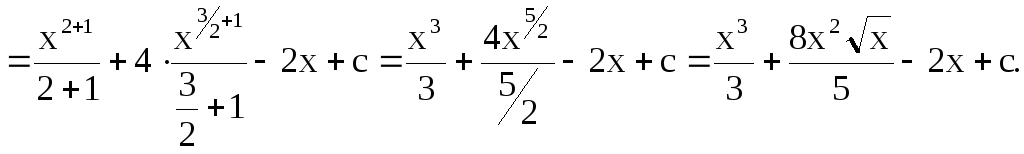
Проверка результата:

Получили подынтегральную функцию, интеграл найден верно.

б) Найти

Известно, что

Пусть

 дифференциал функции u.

Из последнего равенства

Тогда

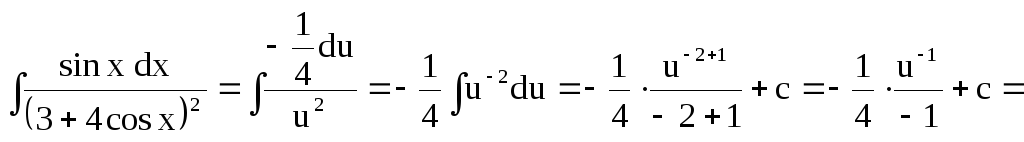
Проверка результата:

Получили подынтегральную функцию, интеграл найден верно.

в) Найти

 правильная рациональная дробь, у которой в числителе записан многочлен первой степени (линейная функция), а в знаменателе  многочлен второй степени (квадратичная функция).

Представим подынтегральную функцию в виде простых дробей методом неопределённых коэффициентов. Вид этих дробей определяется из разложения знаменателя х² + 4х +3 на множители.

Разложим знаменатель х² + 4х +3 на множители, используя формулу

ах² + bx +c = a(x  x₁)(x  x₂), где

х₁ и х₂  корни квадратного уравнения х² + 4х +3 = 0.

Решим это уравнение.

D = 4²  4ּ1ּ3 = 4,

Получим разложение х² + 4х +3 = (х + 1)(х + 3).

Тогда где А и В  неопределённые коэффициенты, которые следует определить.

Приравнивая числители крайних дробей, получим

2х  5 = А(х + 3) + В(х + 1).

Последнее равенство выполняется при всех значениях переменной х.

При х = 1 получим:

7 = А·2, откуда

При х = 3 получим:

11 = В·(2), откуда

Подынтегральная функция является суммой следующих простых дробей:

Тогда

Проверку результата выполните самостоятельно.

Задания 51  60. Вычисление площадей с помощью определённого интеграла

Краткие теоретические сведения

• Формула Ньютона-Лейбница:

где

F(x)  первообразная для функции f(x), т.е. F(x) = f(x).

• Используют сокращенную запись:

• Площадь фигуры, ограниченной кривой у = f(x), осью ОХ и двумя вертикальными прямыми х = а и х = b (a<b), вычисляется по формуле:

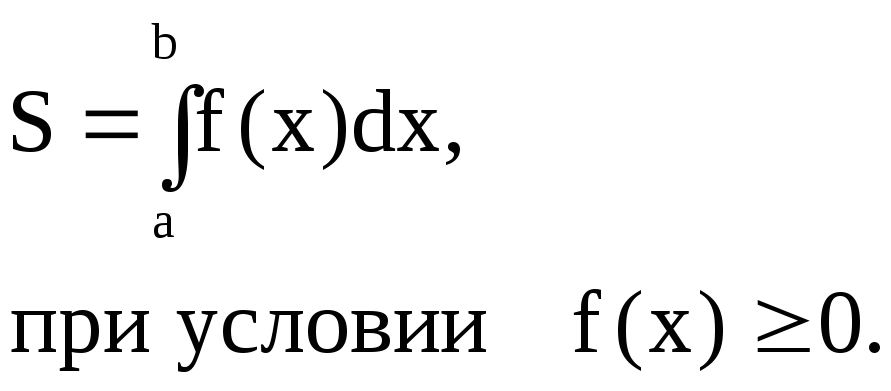
Пример

Вычислить площадь фигуры, ограниченной параболой прямой и осью ОХ. Сделать чертеж.

Решение

Сделаем чертеж.

 уравнение верхней половины параболы х = у²  2 с вершиной А(-2;0), ветви которой направлены вдоль оси ОХ вправо.

 уравнение прямой, проходящей через точку С(1;0).

Найдем координаты точки В пересечения параболы и прямой, решив систему уравнений

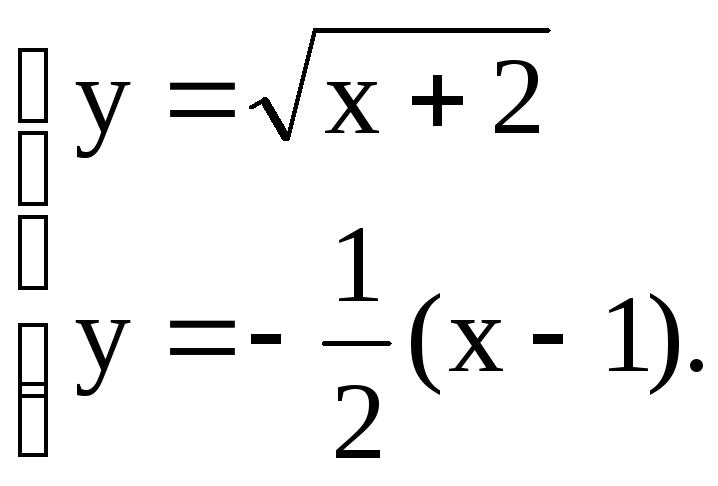
Решим эту систему уравнений.

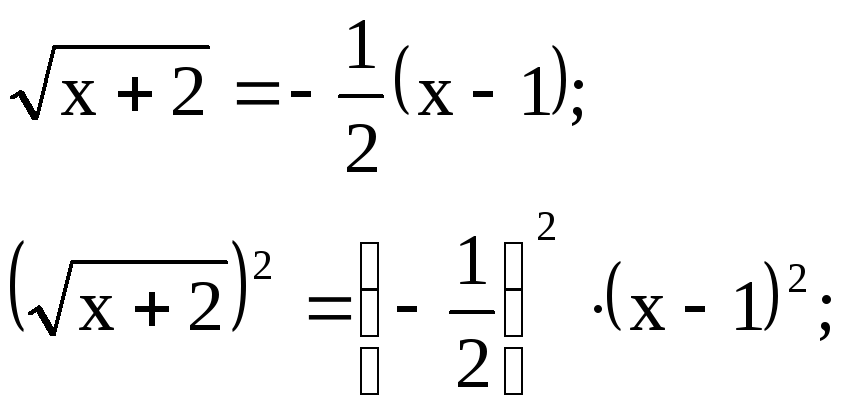
После преобразования последнего уравнения получим:

х²  6х  7 = 0  квадратное уравнение с корнями х₁ = 1, х₂ = 7.

Второй из этих корней является посторонним для исходной системы уравнений.

При х = 1 получим у = 1, т.е. В(1;1)  точка пересечения параболы и прямой.

Кривая, ограничивающая фигуру сверху, не может быть записана единым уравнением (см. чертеж), поэтому разобьем фигуру вертикальной прямой х = 1 на две части с площадями S₁ и S₂.

y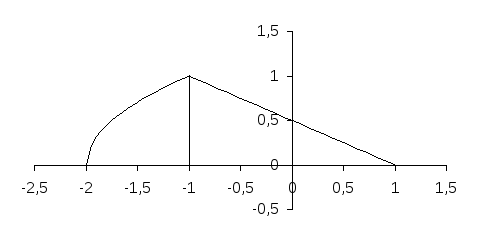

B

S₁

S₂

x

C

A

Получим:

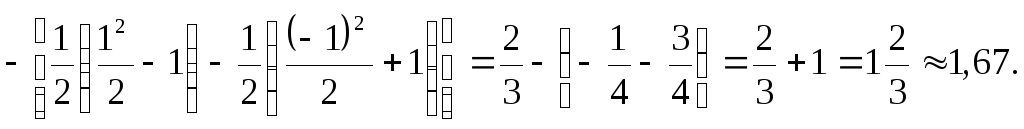
Задания 61  70. Несобственный интеграл

Краткие теоретические сведения

• Несобственный интеграл от непрерывной функции f(x) на бесконечном промежутке [a; +) определяется следующим образом:

• Для вычисления несобственного интеграла применяют формулу:

где

F(x)  первообразная для f(x) и

• Если 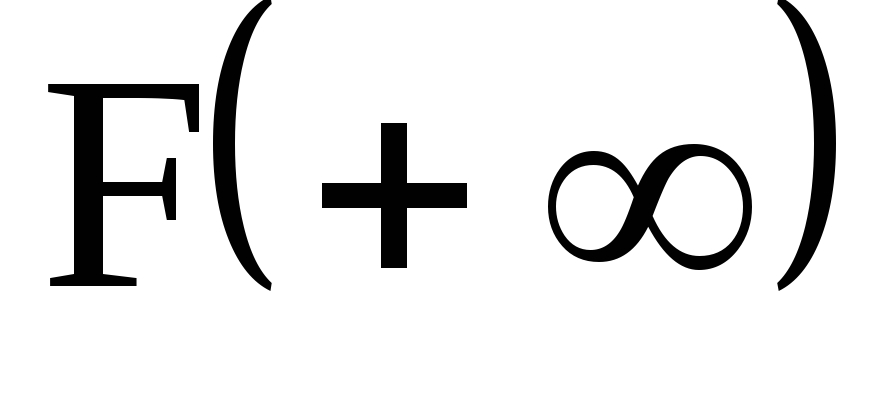 конечное число, то 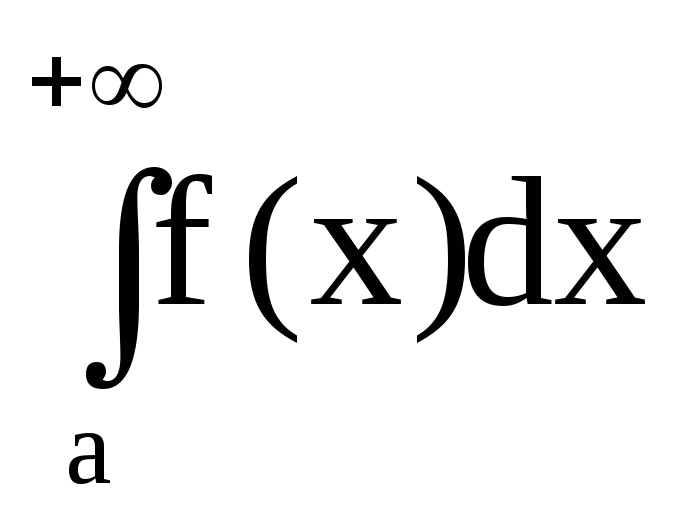сходится, в противном случае 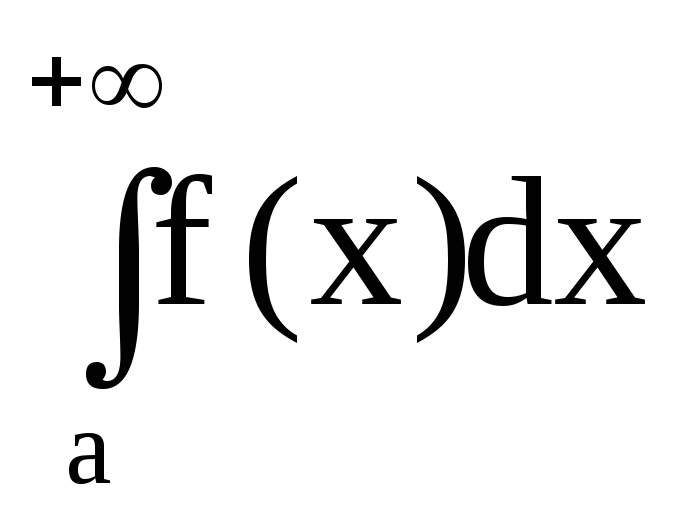расходится.

Пример

Вычислить несобственный интеграл или установить его расходимость.

Решение

а) Найдем неопределённый интеграл

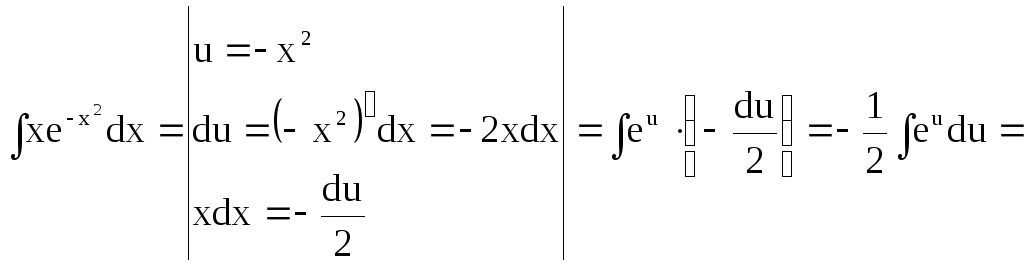
Следовательно,  первообразная для

Несобственный интеграл вычислен и равен следовательно, он сходится.

б) Найдем неопределённый интеграл

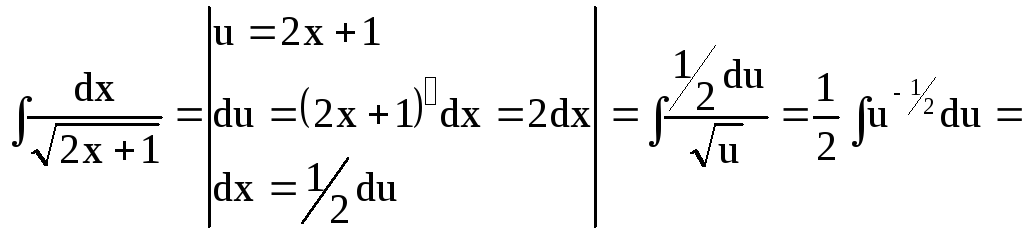
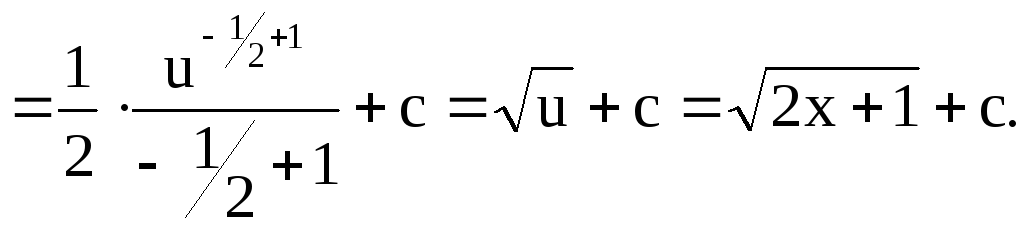
 первообразная для

следовательно,

несобственный интеграл расходится.

Задания 71  80. Непосредственный подсчет вероятностей

Краткие теоретические сведения

• Под испытанием S будем понимать осуществление некоторого комплекса условий или действий, в результате которого происходит определенное явление, называемое событием.

• События бывают следующих видов:

случайные события - это такие события, которые могут произойти, а могут не произойти в результате испытания. Случайные события обозначаются буквами А, В, С и т.д.;

достоверное событие обязательно должно произойти в результате испытания и обозначается U;

невозможное событие не может произойти в результате испытания и обозначается V;

элементарные события - это неразложимые равновозможные исходы испытания, причем появление одного из элементарных событий исключает появление других.

• Те элементарные события, при которых наступает событие А, называются благоприятствующими событию А.

Определение. Вероятность Р(А) события А равна отношению числа т элементарных событий, благоприятствующих событию А, к общему числу п элементарных событий, т.е.

P(A) =

Это определение вероятности события называют классическим.

Следовательно, чтобы вычислить вероятность события А, необходимо:

а) выяснить, какие события являются элементарными и подсчитать их общее число п;

б) выяснить, какие из элементарных событий благоприятствуют событию А, и подсчитать их число т;

в) вычислить Р(А) =

• Свойства вероятностей

1. Достоверное событие U обязательно происходит при испытании, следовательно, ему благоприятствуют все элементарные исходы.

Тогда т = п и P(U)= 1.

2. Невозможное событие V не может произойти в результате испытания, т.е. ему не благоприятствует ни один из элементарных исходов.

Тогда m = 0 и P(V)=0.

3. Для любого события выполняются неравенства 0≤т≤п, следовательно,

0 ≤ Р(А) ≤ 1, т.е. вероятность любого события заключена в пределах от нуля до единицы.

Если вероятность близка к единице, то событие является часто происходящим.

Если вероятность близка к нулю, то событие является редким.

Вероятность принято вычислять в десятичных долях. Достаточна точность вычислений до сотых.

Классическое определение позволяет вычислить вероятность события теоретически, без проведения испытаний. Но в реальных условиях требования конечного числа исходов испытания и равновозможности элементарных исходов редко выполнимы, что ограничивает возможность применения классического определения вероятности.

• Пусть испытание S повторяется n раз и m  число появлений события А в n испытаниях.