Решение
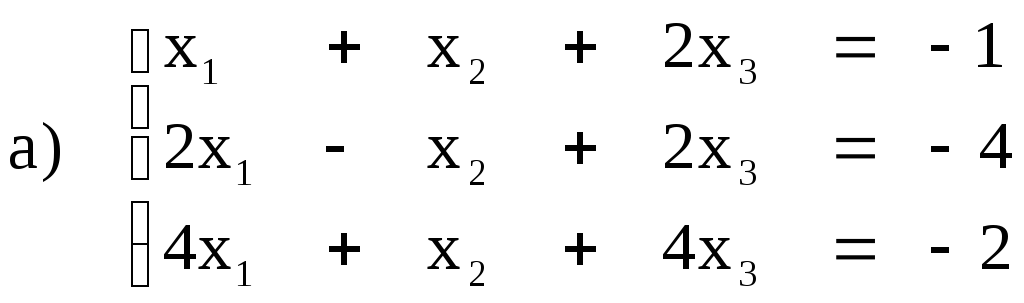
Запишем систему уравнений в виде таблицы Гаусса:
Таблица 1.
-
х1
х2
х3
В
Контроль
1
2
4
1
1
1
2
2
4
1
4
2
3
1
7
Каждый элемент контрольного столбца равен сумме всех предыдущих элементов соответствующей строки:
3 = 1 + 1 + 2 1, 1 = 2 1 + 2 4, 7= 4 + 1 +4 2.
В рамку помещен разрешающий элемент, который равен единице. Соответственно, разрешающими являются первая строка и первый столбец.
Выполним преобразования по методу Жордана-Гаусса, а именно:
-
Разрешающую строку разделим на разрешающий элемент;
-
В разрешающем столбце все элементы, кроме разрешающего, заменим на нули;
-
Остальные элементы таблицы пересчитаем по правилу прямоугольника.
Например, во второй строке последовательно получаем следующие элементы:
Таблица 2.
-
х1
х2
х3
В
Контроль
1
0
0
1
3
3
2
2
4
1
2
2
3
7
5
Контрольный столбец показывает, что вычисления верны, т.к. каждый его элемент равен сумме всех предыдущих элементов соответствующей строки.
Анализируя таблицу 2, замечаем, что х1 исключено из всех уравнений, кроме первого, в котором коэффициент при х1 равен 1.
х1 является базисной переменной.
В таблице 2 отметим рамкой разрешающий элемент, сделаем преобразования по методу Жордана-Гаусса. После этого х2 будет исключено из всех уравнений кроме второго.
Отметим, что преобразования не изменяют столбец при переменной, уже ставшей базисной. В нашем случае неизменным остается первый столбец.
Таблица 3.
-
х1
х2
х3
В
Контроль
1
0
0
0
1
0
2
4
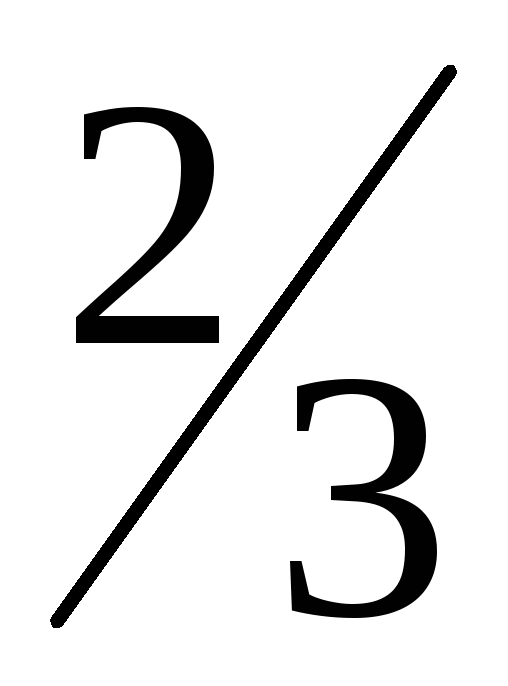
2
Контрольный столбец показывает, что вычисления верны. х2 исключено из всех уравнений, кроме второго, в котором коэффициент при х2 равен единице.
х2 является базисной переменной.
В таблице 3 отметим рамкой разрешающий элемент, сделаем преобразования по методу Жордана-Гаусса, при этом два первых столбца таблицы 3 не изменятся.
Таблица 4.
-
х1
х2
х3
В
Контроль
1
0
0
0
1
0
0
0
1
1
2
2
2
3
1
Таблица 4 соответствует следующей системе уравнений:
Эта система уравнений равносильна исходной и является её единственным решением т.к. все переменные х1, х2, х3 являются базисными.
Обратите внимание, что значения базисных переменных записаны в столбце свободных членов В.
Итак, исходная система уравнений имеет единственное решение (1;2;-2).
Запишем систему уравнений в виде таблицы Гаусса:
Таблица 1.
-
х1
х2
х3
х4
В
Контроль
3
1
2
6
1
5
1
1
0
17
6
11
4
4
0
19
11
8
В рамку помещен разрешающий элемент.
Выполним дважды преобразования по методу Жордана-Гаусса (см. предыдущий пример). Получим таблицы 2 и 3.
Таблица 2.
-
х1
х2
х3
х4
В
Контроль
0
1
0
3
1
3
2
1
2
1
6
1
8
4
8
14
11
14
Таблица 3.
-
х1
Х2
х3
х4
В
Контроль
0
1
0
1
0
0
0
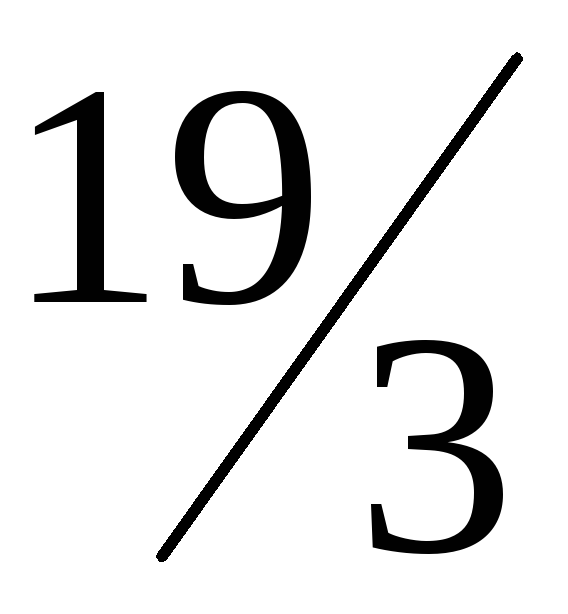
0
0
0
Все элементы последней строки таблицы 3 равны нулю, следовательно, третье уравнение системы является следствием первых двух и его следует исключить из дальнейшего рассмотрения.
По таблице 3 восстановим два первых уравнения системы:
Откуда
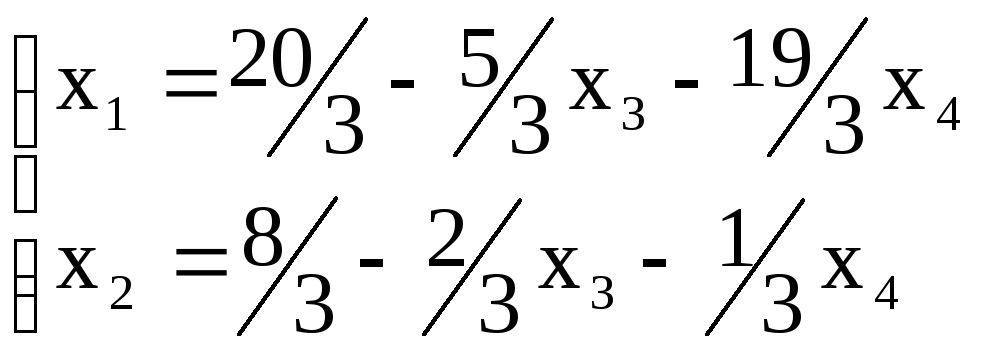
общее
решение системы уравнений,
где х3, х4 свободные переменные,
х1, х2 базисные переменные.
Если
х3 = х4 = 0, то х1 =
,
х2 =
Получим
(
;
;
0; 0) базисное решение.
Это базисное решение является допустимым, т.к. не содержит отрицательных компонент, и невырожденным, т.к. значения базисных переменных отличны от нуля.
Обратите внимание, что базисное решение определяется по столбцу В свободных членов таблицы 3:
если
х3 = х4 = 0, то х1 =
,
х2 =
Именно эти значения базисных переменных
записаны в столбце В.
Перейдем к другому базисному решению. Для этого, например, переменную х3 переведем в базисные, а переменную х2 в свободные.
Разрешающими станут третий столбец и первая строка, разрешающий элемент в таблице 3 выделен рамкой.
Выполним преобразования по методу Жордана-Гаусса:
Таблица 4.
-
х1
х2
х3
х4
В
Контроль
0
1
1
0
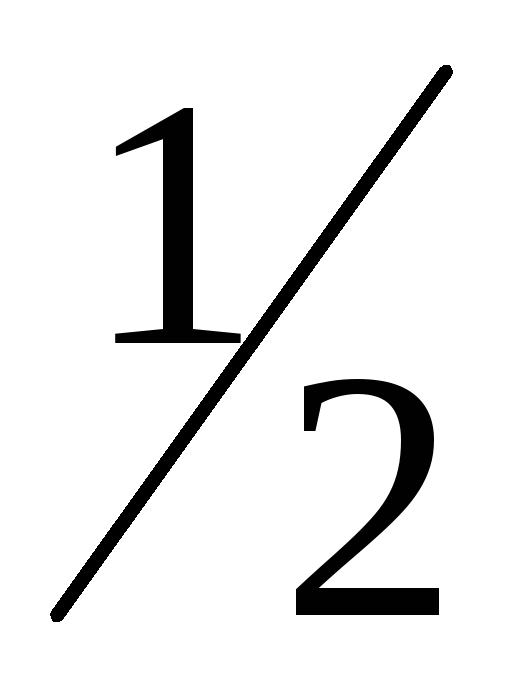
4
0
7
4
В таблице 4 осталось только две строки, т.к. третье уравнение исключено из рассмотрения.
Анализ таблицы 4 показывает, что х2, х4 свободные переменные, а х1, х3 базисные.
Если х2 = х4 = 0, то по столбцу В свободных членов определим значения базисных переменных: х3 = 4, х1 = 0.
Получим (0; 0; 4; 0) базисное решение, допустимое и вырожденное, т.к. одна из базисных переменных х1 равна нулю.
Запишем систему уравнений в виде таблицы Гаусса:
Таблица 1.
-
х1
х2
х3
х4
В
Контроль
3
1
2
6
1
5
1
1
0
17
6
11
4
4
2
19
11
10
В рамку помещен разрешающий элемент.
Выполним дважды преобразования по методу Жордана-Гаусса:
Таблица 2.
-
х1
х2
х3
х4
В
Контроль
0
1
0
3
1
3
2
1
2
1
6
1
8
4
6
14
11
12
Таблица 3.
-
х1
х2
х3
х4
В
Контроль
0
1
0
1
0
0
0
0
6
6
Все элементы последней строки таблицы 3, кроме двух последних равны нулю. Такая система несовместна, т.е. не имеет решений.