Задания 151  160. Задачи линейного программирования Краткие теоретические сведения

• Математическая модель многих экономических задач имеет следующий вид:

Найти максимум или минимум целевой функции

F = c₁x₁ + c₂x₂ +…+ c_nx_n при ограничениях:

Рассмотрим лишь случай нахождения максимума функции F, т.к. нахождение минимума сводится к нахождению максимума функции Z =  F.

Для простоты ограничимся случаем, когда свободные члены неравенств-ограничений неотрицательны, т.е. b_i ≥ 0, i = 1, 2, …, m.

Отметим, что числа m и n между собой не связаны.

• При n = 2 решения системы неравенств-ограничений образуют выпуклый многоугольник на плоскости.

Многоугольник называется выпуклым если вместе с двумя своими точками содержит отрезок прямой, соединяющий эти точки.

Вершины выпуклого многоугольника называются угловыми точками.

• Неравенства-ограничения сводятся к уравнениям-ограничениям введением дополнительных переменных х_n+1, х_n+2, …, х_n+m следующим образом:

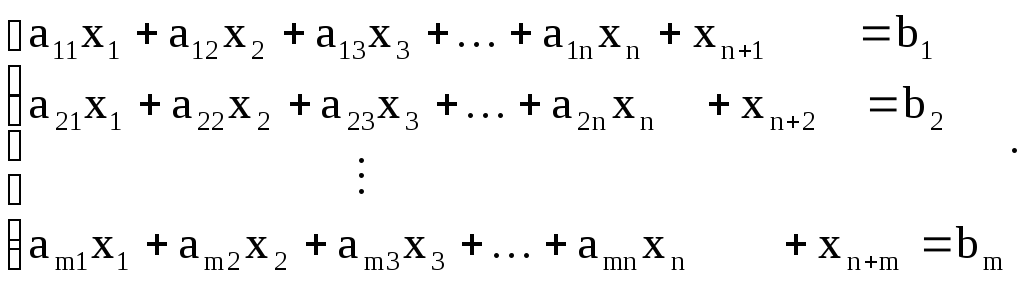
При условии неотрицательности свободных членов b₁, b₂, …, b_m неравенств-ограничений дополнительные переменные тоже неотрицательны.

Дополнительные переменные имеют конкретный экономический смысл.

В целевую функцию F также следует ввести дополнительные переменные с нулевыми коэффициентами, т.е.

F = c₁x₁ + c₂x₂ +…+ c_nx_n + 0ּx_n+1 + 0ּx_n+2 +…+ 0ּx_n+m.

• Каноническая задача линейного программирования имеет следующий вид:

Найти максимум целевой функции

F = c₁x₁ + c₂x₂ +…+ c_nx_n при ограничениях:

• Неотрицательные решения системы уравнений-ограничений образуют выпуклое множество в n-мерном пространстве. Угловыми точками этого множества являются допустимые базисные решения системы уравнений-ограничений.

• Планом задачи называется любое решение системы ограничений.

• Опорным планом называется угловая точка выпуклого множества решений системы ограничений.

• Оптимальным планом называется такой план, на котором целевая функция F принимает оптимальное значение, т.е. максимальное при нахождении максимума и минимальное при нахождении минимума.

• Если n = 2, то задачу линейного программирования можно решить геометрически.

Пусть нужно найти максимум целевой функции

F = c₁x₁ + c₂x₂ при ограничениях:

1) Каждое линейное неравенство-ограничение в системе координат ОХ₁Х₂ определяет полуплоскость.

Действительно, линейное неравенство Ax + By ≤ C после преобразований может быть приведено к одному из следующих четырех видов: x ≤ a, x ≥ a, y ≤ kx + b, y ≥ kx + b.

Первые два неравенства определяют полуплоскость, лежащую, соответственно, слева или справа от прямой x = а вместе с ограничивающей прямой.

Вторые два неравенства определяют полуплоскость, лежащую, соответственно, ниже или выше прямой y = kx + b вместе с ограничивающей прямой.

Зная, что линейное неравенство определяет полуплоскость, можно установить, как расположена эта полуплоскость, не выполняя преобразований неравенства. Сначала следует построить прямую, ограничивающую полуплоскость. Затем произвольным образом выбрать контрольную точку в одной из полуплоскостей и подставить её координаты в неравенство. Если в результате получится верное числовое неравенство, то контрольная точка принадлежит искомой полуплоскости. Если же получится неверное неравенство, то искомой является другая полуплоскость.

В качестве контрольной обычно выбирают точку О(0;0).

Решения системы линейных неравенств-ограничений образуют в системе координат ОХ₁Х₂ выпуклый многоугольник, который является пересечением полуплоскостей, определяемых неравенствами.

Построим многоугольник решений системы неравенств-ограничений.

2) Уравнение c₁x₁ + c₂x₂ = р (р = const) определяет прямую, на которой значение целевой функции постоянно и равно р.

Построим прямую L₀, определяемую уравнением c₁x₁ + c₂x₂ = 0. Прямая L₀ проходит через начало координат, причем F = 0 на L₀.

3)  вектор нормали к прямой L₀. При параллельном перемещении прямой L₀ в направлении вектора значение целевой функции F увеличивается. При этом максимальное значение функция F принимает в точке многоугольника решений, наиболее удаленной от L₀.

• Выводы из геометрического решения задач линейного программирования.

1. Если оптимальный план существует, то он находится не внутри, а на границе многоугольника решений.

2. Если оптимальный план единственен, то он совпадает с одной из угловых точек многоугольника решений (рис. 1).

3. Если оптимальных планов множество, то они совпадают с одной из сторон многоугольника решений (рис. 2).

4. Если оптимальный план не существует, то система неравенств противоречива или определяет неограниченный многоугольник решений (рис. 3).

• Симплекс-метод  самый общий метод решения задач линейного программирования (simplex  простейший). При его использовании задача линейного программирования должна быть приведена к каноническому виду:

Найти максимум целевой функции

F = c₁x₁ + c₂x₂ +…+ c_nx_n при ограничениях:

• Сущность симплекс-метода заключается в следующем.

Известно, что неотрицательные решения системы уравнений-ограничений образуют выпуклое множество, причем допустимые базисные решения являются его угловыми точками, или опорными планами.

Симплекс-метод осуществляет целенаправленный перебор опорных планов так, что на каждом следующем опорном плане значение целевой функции F улучшается. Если оптимальный план существует, то он будет достигнут.

• Критерий оптимальности плана.

Для каждого полученного опорного плана т.е. для допустимого базисного решения вычисляются оценки z_j по формуле:

где

 коэффициенты целевой функции F при базисных переменных;

 соответствующие коэффициенты при переменной x_j, вычисленные в результате преобразования системы уравнений-ограничений по методу Жордана-Гаусса.

Если z_j ≤ 0 при всех j = 1, 2, …, n, то план является оптимальным.

Оценки z_j проще вычислять следующим образом.

Для базисных переменных эти оценки равны нулю, а для свободных переменных их можно вычислять по правилу прямоугольника.

• Переход к новому улучшенному опорному плану осуществляется следующим образом.

Если построенный план не является оптимальным, то одну из свободных переменных, которой соответствует положительная оценка z_j следует перевести в базисные. Рекомендуется переводить в базисные ту из свободных переменных, которой соответствует наибольшая положительная оценка, что позволяет сократить процесс нахождения оптимального плана.

Чтобы определить базисную переменную, которую следует перевести в свободные, вычисляют оценочные отношения _i по формуле:

_i = , где

b_i  элементы столбца свободных членов;

a_ik  коэффициенты при свободной переменной x_k, которую надлежит перевести в базисные.

_i вычисляется только для тех значений i, для которых a_ik >0.

Переводится в свободные та базисная переменная, для которой соответствующее оценочное отношение _i минимально, что обеспечивает допустимость следующего базисного решения системы уравнений-ограничений.

Пример

Предприятие оптовой торговли закупает для реализации товары двух видов. Известно, что при реализации товаров первого и второго вида в расчете на одну тысячу рублей затраты рабочего времени на обслуживание покупателей в среднем составляют 2 ч. и 3 ч., издержки обращения  60 руб. и 30 руб. соответственно.

Резерв времени для реализации товара составляет 780 часов, издержки обращения не должны превышать 14,4 тыс.руб. Прибыль от реализации товаров первого и второго вида составляет 16% и 20% соответственно.

Определить наибольшую прибыль, которую может получить торговое предприятие, если на закупку может быть истрачено не более 300 тыс. руб.

а) Составить математическую модель задачи;

б) решить задачу геометрически;

в) решить задачу симплекс-методом.