Решение

а) Составим математическую модель задачи.

Пусть предприятие закупило товаров первого и второго вида на x₁ тыс. руб. и x₂ тыс. руб. соответственно.

Прибыль от реализации товаров первого и второго вида составляет 16% и 20% от их стоимости, т.е. 0,16х₁ тыс. руб. и 0,2х₂ тыс. руб. соответственно.

Тогда общая прибыль  0,16х₁ + 0,2х₂ тыс. руб. Следовательно,

F = 0,16х₁ + 0,2х₂  целевая функция,

Т.к. на закупку товаров может быть истрачено не более 300 тыс. руб., то

х₁ + х₂  300.

Затраты времени на обслуживание покупателей для товаров первого вида составляют 2х₁ часов, а для товаров второго вида  3х₂ часов. Общие затраты времени составляют 2х₁ + 3х₂ часов. Резерв времени составляет 780 часов, следовательно,

2х₁ + 3х₂  780.

Издержки обращения для товаров первого вида составляют 60х₁ руб., а для товаров второго вида  30х₂ руб. Общие издержки обращения не должны превышать 14400 руб., следовательно,

60х₁ + 30х₂  14400.

Математическая модель задачи имеет следующий вид:

Найти максимум целевой функции

F = 0,16х₁ + 0,2х₂ при ограничениях:

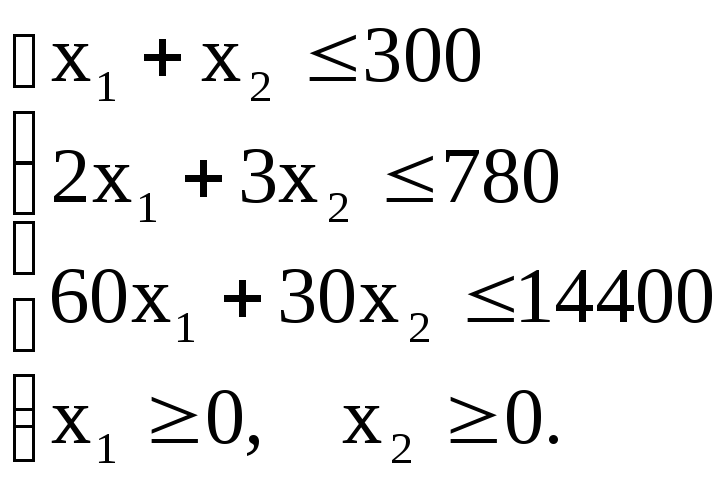
б) Решим задачу геометрически.

В системе координат ОX₁X₂ построим многоугольник решений системы неравенств-ограничений.

Каждое неравенство-ограничение является линейным, следовательно, оно определяет полуплоскость, ограниченную соответствующей прямой.

1. х₁ + х₂  300.

х₁ + х₂ = 300  уравнение граничной прямой.

Построим эту прямую по двум точкам:

если х₁ = 0, то х₂ = 300;

если х₂ = 0, то х₁ = 300.

Граничная прямая проходит через точки (0; 300) и (300; 0).

Поставим в неравенство координаты контрольной точки О(0; 0), получим 0  300  верное числовое неравенство.

Следовательно, неравенство х₁ + х₂  300 определяет полуплоскость, расположенную под прямой х₁ + х₂ = 300 (см. чертеж).

2) 2х₁ + 3х₂  780.

2х₁ + 3х₂ = 780  уравнение граничной прямой.

если х₁ = 0, то х₂ = = 260;

если х₂ = 0, то х₁ = = 390.

Прямая проходит через точки (0; 260) и (390; 0).

Подставим в неравенство координаты контрольной точки О(0; 0):

0  780  верное неравенство.

Следовательно, неравенство 2х₁ + 3х₂  780 определяет полуплоскость, расположенную под прямой 2х₁ + 3х₂ = 780.

3) 60х₁ + 30х₂  14400.

60х₁ + 30х₂ = 14400  уравнение граничной прямой.

если х₁ = 0, то х₂ = = 480;

если х₂ = 0, то х₁ = = 240.

Прямая проходит через точки (0; 480) и (240; 0).

Подставим в неравенство координаты контрольной точки О(0; 0):

0  780  верное неравенство.

Следовательно, неравенство 60х₁ + 30х₂  14400 определяет полуплоскость, расположенную под прямой 60х₁ + 30х₂ = 14400.

4) х₁  0, х₂  0.

Эти неравенства показывают, что решения системы неравенств-ограничений неотрицательны, т.е. находятся в правом верхнем координатном углу.

Пересечение полуплоскостей, определяемых неравенствами-ограничениями, образует выпуклый многоугольник OABCD (см. чертеж).

2х₁ + 3х₂ = 780  уравнение прямой АВ;

х₁ + х₂ = 300  уравнение прямой ВС;

60х₁ + 30х₂ = 14400  уравнение прямой CD.

5) F = 0,16х₁ + 0,2х₂  целевая функция.

Построим прямую L₀: 0,16х₁ + 0,2х₂ = 0 по двум точкам:

если х₁ = 0, то х₂ = 0;

если х₁ = 50, то х₂ = 40.

Прямая L₀ проходит через точки (0; 0) и (50; 40).

На прямой L₀ функция F принимает значение, равное нулю.

{0,16; 0,2}  вектор нормали к прямой L₀, однако, модуль этого вектора мал, поэтому удобнее построить вектор большей длины, имеющий то же направление, что и вектор {0,16; 0,2}.

 вектор нормали к L₀. Проверьте, что

При параллельном перемещении прямой L₀ в направлении вектора значение целевой функции F увеличивается и достигает своего максимального значения в точке многоугольника решений, наиболее удаленной от прямой L₀. Из чертежа видно, что таковой является точка B.

Координаты точки B являются решением системы уравнений, определяющих прямые АВ и ВС:

Домножим второе уравнение на 2 и почленно вычтем из первого, получим:

х₂ = 780  2ּ300=180,

х₁=300  180 = 120.

(120; 180)  координаты точки В.

F(B) = 0,16ּ120 + 0,2ּ180 = 55,2.

Проверьте, что F(A) = 41,6; F(C) = 52,8; F(D) = 52. Координаты точки С найдите самостоятельно.

Таким образом, наибольшая прибыль, которую может получить торговое предприятие, составляет 55,2 тыс. руб. При этом следует закупить товаров первого и второго вида на 120 тыс. руб. и 180 тыс. руб. соответственно.

в) Решим задачу симплекс-методом.

По системе неравенств-ограничений введем дополнительные переменные х₃, х₄, х₅ следующим образом:

х₃ = 300  (х₁ + х₂);

х₄ = 780  (2х₁ + 3х₂);

х₅= 14400  (60х₁ + 30х₂).

Ясно, что х₃ ≥ 0, х₄ ≥ 0, х₅ ≥ 0.

Дополнительные переменные имеют конкретный экономический смысл, а именно:

х₃  денежные средства, оставшиеся после закупки товаров;

х₄  резерв времени, неиспользованный после реализации товаров;

х₅  экономия издержек обращения

Введением дополнительных переменных неравенства-ограничения преобразуются в уравнения-ограничения:

х_i ≥ 0, i = 1, 2, 3, 4, 5.

Целевая функция с учетом дополнительных переменных принимает вид:

F = 0,16х₁ + 0,2х₂ + 0х₃ + 0х₄ + 0х₅.

Следует найти максимум целевой функции F при наложенных уравнениях-ограничениях и при условии неотрицательности переменных х₁, х₂, х₃, х₄, х₅.

Решение удобно оформлять в виде симплекс-таблиц.

Таблица 1

	Cj	0,16	0,2	0	0	0	В	θi
Cб	xj xб	х1	x2	X3	x4	x5
0	x3	1	1	1	0	0	300	300
0	x4	2	3	0	1	0	780	260
0	x5	60	30	0	0	1	14400	480
Zj		0,16	0,2	0	0	0	F = 0

Шесть столбцов таблицы, начиная с третьего, заполняет таблица Гаусса для системы уравнений-ограничений, в верхней строке указаны коэффициенты с_j целевой функции F при переменных x_j, j = 1, 2, 3, 4, 5.

Последний столбец предназначен для вычисления оценочных отношений θ_i, i = 1, 2, 3.

Последняя строка  для вычисления оценок Z_j, j = 1, 2, 3, 4, 5.

Второй столбец таблицы обозначен символом x_б: в нем на каждом этапе преобразований указываются базисные переменные системы уравнений. Ясно, что на начальном этапе базисными переменными являются x₃, x₄, x₅. Будем называть набор этих переменных базисом.

В первом столбце С_б указаны коэффициенты целевой функции F при соответствующих базисных переменных. В таблице 1 столбец С_б нулевой, т.к. базисными являются дополнительные переменные.

Известно, что целевая функция F достигает своего оптимального значения на одном из опорных планов, т.е. на допустимом базисном решении системы уравнений-ограничений. В базисном решении свободные переменные равны нулю, а базисные переменные равны соответствующим элементам столбца В свободных членов. При этом значение функции F вычисляется по формуле:

где

r  число базисных переменных;

b_i  элемент столбца В, i = 1, 2, …, r;

C_бi  элемент первого столбца таблицы, i = 1, 2, …, r.

На начальном шаге F = 0ּ300 + 0ּ780 + 0ּ14400 = 0.

Проведем проверку оптимальности плана. Для этого вычислим оценки Z_j, и поместим их в последней строке оценок.

На начальном шаге Z_j = c_j, j = 1, 2, 3, 4, 5.

Если Z_j ≤ 0 при всех j, то план оптимальный.

Мы имеем две положительные оценки Z₁=0,16 и Z₂=0,2, следовательно, план не является оптимальным.

Перейдем к новому улучшенному опорному плану. Ведем в базис x₂, т.к. этой переменной соответствует наибольшая положительная оценка.

Чтобы определить переменную, которую следует вывести из базиса, вычислим оценочные отношения

θ_i = i = 1, 2, 3, где

b_i  элементы столбца В,

 элементы столбца коэффициентов при x₂ для > 0.

Получим:

θ₁ =

θ₂ =

θ₃ =

Значения θ₁, θ₂, θ₃ впишем в последний столбец таблицы 1.

Минимальное оценочное отношение θ₂=260, этому значению соответствует по строке базисная переменная х₄. Следовательно, х₂ следует ввести в базис вместо х₄.

Для нахождения нового опорного плана преобразуем систему уравнений-ограничений по методу Жордана-Гаусса. В таблице 1 в рамку помещен разрешающий элемент, он равен 3.

Далее пересчитаем все элементы таблицы, включая строку оценок z_j, но не затрагивая столбец оценочных отношений θ_i, по методу Жордана-Гаусса. В первом столбце поместим коэффициенты целевой функции F при базисных переменны х₃, x₂, x₅ соответственно.

Получим следующую таблицу:

Таблица 2

	Cj	0,16	0,2	0	0	0	В	θi
Cб	xj xб	х1	x2	x3	х4	x5
0	x3	1/3	0	1	1/3	0	40	120
0,2	x2	2/3	1	0	1/3	0	26	390
0	x5	40	0	0	1	1	6600	165
Zj		2/75	0	0	1/15	0	F = 52

= 0ּ40 + 0,2ּ260 + 0ּ6600 = 52,

Значение целевой функции увеличилось и равно её значению в точке D (260; 0) многоугольника решений (см. решение задачи геометрическим методом).

Проверим оптимальность построенного плана.

Оценки Z_j для базисных переменных х₂, х₃, х₅ равны 0, оставшиеся две оценки вычислены по правилу прямоугольника.

следовательно, план не является оптимальным.

Перейдем к следующему опорному плану.

Свободную переменную х₁ следует ввести в базис.

Чтобы определить переменную, которую следует вывести из базиса, вычислим оценочные отношения θ_i, как это было сделано ранее:

θ₁ =

θ₂ =

θ₃ = 6600:40 = 165.

θ₁ = 120  минимальное оценочное отношение, следовательно, из базиса следует вывести переменную х₃.

Вновь проведем преобразования по методу Жордана-Гаусса.

Разрешающий элемент в таблице 2 отмечен рамкой, он равен 1/3 .

Получим следующую таблицу:

Таблица 3

	Cj	0,16	0,2	0	0	0	В	θi
Cб	xj xб	х1	x2	x3	x4	x5
0,16	х1	1	0	3	1	0	120
0,2	x2	0	1	2	1	0	180
0	x5	0	0	120	39	1	1800
Zj		0	0	2/25	1/25	0	F = 55,2

= 0,16ּ120 + 0,2ּ180 = 55,2.

Найденное значение целевой функции F соответствует её значению в точке В (120; 180) многоугольника решений.

Строка оценок Z_j не содержит ни одной положительной оценки, следовательно, найденный план является оптимальным.

Вывод

Торговое предприятие получит максимальную возможную прибыль, равную 55,2 тыс. руб., если товаров первого вида будет закуплено на 120 тыс. руб. (х₁ = 120), а товаров второго вида  на 180 тыс. руб. (х₂ = 180). При этом все средства на закупку товара будут исчерпаны (х₃ = 0), рабочее время истрачено полностью (х₄=0), окажется экономия издержек обращения на сумму в 1800 руб. (х₅ = 1800).