Задания 121130. Статистические оценки параметров распределения Краткие теоретические сведения

• Генеральная совокупность X некоторого количественного признака однородных объектов изучается при помощи случайной выборки.

Пусть из генеральной совокупности извлечена выборка, причем х₁ встретилось n₁ раз, x₂ встретилось n₂ раз, ..., x_k встретилось n_k раз. Наблюдаемые значения х₁, x₂, …, x_k, расположенные в возрастающем порядке, называют вариантами; n₁, n₂, …, n_k называют частотами.

Статистическое распределение выборки имеет вид таблицы, в верхней строке которой записаны все варианты в возрастающей последовательно­сти, а в нижней  соответствующие частоты.

В общем виде это выглядит так:

х1	x2	…	xk
n1	n2	…	nk

Сумма всех частот с учетом повторов равна количеству всех вариант выборки, т.е.

Число n называют объемом выборки.

Вместо частот можно рассматривать относительные частоты

Относительные частоты имеют свойства вероятностей, а именно:

Если относительная частота близка к 1, то соответствующая варианта встречается часто, если же относительная частота близка к 0, то соответствующая варианта встречается редко.

Для относительных частот выполняется равенство:

Вместо вариант в статистическом распределении выборки можно за­дать последовательность интервалов равной длины, в которые попадают наблюдаемые значения признака. В качестве частоты, соответствующей интервалу, принимают сумму частот всех вариант, попавших в этот интервал. При статистическом анализе интервального распределения выборки все вари­анты, попавшие в один и тот же интервал, переименовываются: всем им присваивается единое значение, равное середине интервала. Это возмож­но в силу незначительного отличия вариант, попавших в один и тот же интервал.

Для наглядности статистическое распределение выборки можно изобразить графически при помощи полигона или гистограммы.

• Полигоном частот называют ломаную линию, соединяющую точки (x_l; n₁), (x₂; n₂), …, (x_k; n_k), при этом по оси абсцисс откладываются варианты х₁, х₂, ..., x_k, а по оси ординат - соответствующие частоты n₁, n₂, …, n_k.

• Полигоном относительных частот называют ломаную линию, соеди­няющую точки (x_l; w₁), (x₂; w₂), …, (x_k; w_k).

• Если статистическое распределение выборки задано при помощи последо­вательности интервалов, то целесообразно построить гистограмму частот или гистограмму относительных частот.

Для этого по оси абс­цисс откладываются интервалы, в которые попадают наблюдаемые значе­ния признака, и на этих интервалах как на основаниях строятся прямо­угольники, высоты которых равны соответствующим частотам n_i или от­носительным частотам w_i. Совокупность прямоугольников образует сту­пенчатую фигуру, называемую гистограммой.

Генеральную совокупность можно рассматривать как значения некото­рой случайной величины X, имеющей определенный вид распределения.

К параметрам распределения относятся математическое ожидание, дисперсия, среднее квадратическое отклонение и другие характеристики.

• Точечная оценка параметра распределения - это некоторая функция, значение которой вычисляется по данным выборки и представляет из себя приближенное значение оцениваемого параметра. Точечная оценка опре­деляется одним числом, или точкой.

• Генеральной средней называют среднее арифметическое значений генеральной совокупности. Если рассматривать генеральную совокупность как значения случай­ной величины X, то математическое ожидание этой случайной величины совпадает с генеральной средней, т.е. = М(Х).

Точечной оценкой для генеральной средней является выбороч­ная средняя , вычисляемая по одной из равносильных формул:

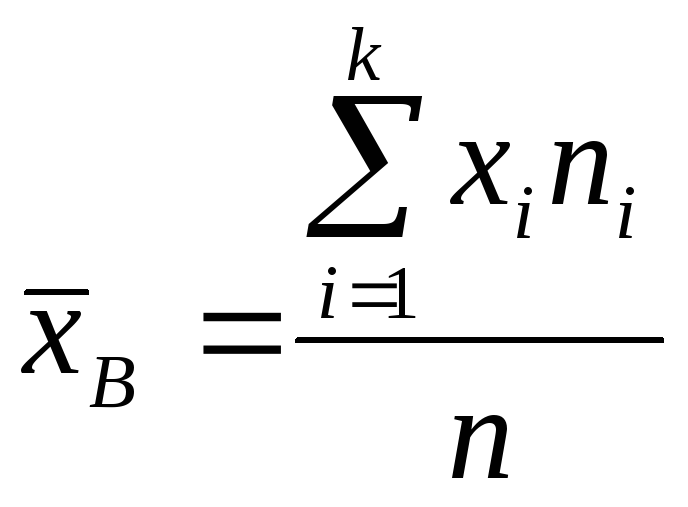или

• Разброс выборочных данных оценивается различно для малых (n < 30) и больших ( n  30 ) выборок.

а) для малых выборок точечной оценкой для генерального среднего квадратического откло­нения σ_Г является "исправленное" стандартное отклонение S(X), ко­торое определяется формулой:

S(X) характеризует абсолютный разброс выборочных данных вокруг среднего выборочного .

Коэффициент вариации V характеризует относительный разброс выборочных данных в процентах вокруг среднего выборочного:

б) для больших выборок точечной оценкой для генерального среднего квадратического откло­нения σ_Г является выборочное стандартное отклонение σ_В, которое вычисляется по одной из равносильных формул:

или

 коэффициент вариации.

Как и для малых выборок, σ_В и V характеризуют абсолютный и относительный разброс выборочных данных вокруг среднего выборочного .

• Точечная оценка параметра генеральной совокупности, особенно при вы­борке малого объема, может существенно отличаться от оцениваемого параметра и приводить к грубым ошибкам. По этой причине используют интервальные оценки.

Интервальная оценка неизвестного параметра распределения представляет из себя доверительный интервал, в который с заданной надежностью попадает оцениваемый параметр.

Границы доверительного интервала вычисляются по выборке.

Доверительный интервал для оценки генеральной средней а нормального распределения имеет вид:

∆ < a < +∆ где

среднее выборочное;

∆  точность оценки.

Точность оценки ∆ находится следующим образом:

а) для малых выборок

∆ = Т(n,γ) где

Т(n,γ)  коэффициент доверия, значения которого для выборки объема n и заданной надежности γ находятся по таблице (приложение 3).

б) для больших выборок

∆ = t_γ где

t_γ  коэффициент, значения которого для заданной надежности γ находятся по таблице значений функции Лапласа ( приложение 2), а именно: t_γ является решением уравнения

Пример

В лаборатории прядильного комбината для проверки кре­пости нити пряжи "Тюльпан" случайным образом было отобрано 90 клубков пряжи. Распределение нитей по крепости приведено в таблице.

Крепость нити, г	170190	190210	210230	230250	250270	270290
Количество нитей	5	18	36	27	3	1

1) Провести первичную обработку результатов наблюдений, а именно: построить гистограмму относительных частот; определить по выборке среднюю крепость нити, оценить абсолютный и относительный разброс крепости нити отобранных клубков пряжи.

2) Полагая, что крепость нити распределена по нормальному закону, и ис­пользуя полученные результаты, найти доверительный интервал, в котором заключена средняя крепость нити с надежностью 0,95.