
- •Раздел 1. Основные понятия теории автоматического управления. Типовые звенья линейных систем автоматического управления. Соединение линейных звеньев
- •1.1 Основные принципы и понятия автоматического управления
- •1.2 Примеры систем автоматического управления
- •1.3 Основные понятия операционного исчисления. Преобразование Фурье и Лапласа
- •Связь преобразований Фурье и Лапласа
- •1.4 Прохождение регулярных сигналов через линейное звено
- •Регулярные сигналы
- •1.5 Характеристики линейного звена
- •1.6 Устойчивость линейных звеньев. Минимально-фазовые звенья. Преобразование произвольного сигнала линейным звеном
- •1.7 Типовые динамические звенья. Простейшие звенья. Звенья первого порядка
- •Простейшие звенья
- •Звенья первого порядка
- •1.8 Колебательные звенья. Особые звенья: неминимально-фазовые устойчивые звенья, неустойчивые звенья
- •Устойчивые неминимально-фазовые звенья
- •Неустойчивые звенья
- •1.9 Особые звенья: иррациональные и трансцендентные звенья Иррациональные звенья
- •Трансцендентные звенья
- •1.8 Соединение линейных звеньев. Преобразование структурных схем
- •Последовательное соединение звеньев
- •Параллельное согласное соединение звеньев
- •Параллельное встречное соединение звеньев
- •Преобразование структурных схем
- •Раздел 2. Исследование устойчивости линейных систем автоматического управления. Качество процессов управления
- •2.1 Постановка задачи исследования устойчивости линейных систем автоматического управления. Алгебраические критерии устойчивости. Критерий Рауса, критерий Гурвица
- •Алгебраические критерии устойчивости
- •2.2 Частотные критерии устойчивости. Критерий Михайлова. Критерий Найквиста
- •2.3 Влияние параметров системы на её устойчивость. Метод d-разбиения
- •Разбиение по одному (комплексному) параметру
- •2.4 Показатели качества процессов управления
- •2.5 Качество регулирования при стандартных воздействиях
- •2.6 Косвенные методы исследования качества процессов управления. Интегральные оценки качества переходных процессов
Трансцендентные звенья
Звено с распределенными параметрами, описываемое одномерным телеграфным уравнением Даламбера
![]() (1.7.106)
(1.7.106)
где
![]() — величина, зависящая от пространственной
координаты r и времени
t, имеет трансцендентную
передаточную функцию, которая зависит
от граничных условий и места снятия
выходного сигнала.
— величина, зависящая от пространственной
координаты r и времени
t, имеет трансцендентную
передаточную функцию, которая зависит
от граничных условий и места снятия
выходного сигнала.
Рассматривая зависящий от пространственной координаты фазор
![]() (1.7.107)
(1.7.107)
можно уравнение (1.7.106) привести к виду
![]() (1.7.108)
(1.7.108)
Корни
характеристического уравнения
![]() — мнимые
— мнимые
![]() (1.7.109)
(1.7.109)
где
![]() .
.
Решение уравнения (1.7.108) можно записать как
![]() (1.7.110)
(1.7.110)
где
![]() и
и
![]() — коэффициенты, зависящие от граничных
условий. Первое слагаемое выражает
волну, движущуюся в сторону возрастания
r, второе — обратную
волну, движущуюся в сторону убывания
r.
— коэффициенты, зависящие от граничных
условий. Первое слагаемое выражает
волну, движущуюся в сторону возрастания
r, второе — обратную
волну, движущуюся в сторону убывания
r.
Звено запаздывания.
Ограничимся рассмотрением таких
объектов, в которых имеется только одна
волна, движущаяся в сторону возрастания
r. Тогда
![]() и
и
![]() (1.7.111)
(1.7.111)
Наиболее
распространенным случаем является
приложение входного воздействия при
![]() ,
т.е.
,
т.е.
![]() ,
и снятие выходного сигнала при
,
и снятие выходного сигнала при
![]() ,
т.е.
,
т.е.
![]() .
В таком случае
.
В таком случае
![]() ,
,
![]() и
и
![]() (1.7.112)
(1.7.112)
где
![]() — время запаздывания.
— время запаздывания.
Если
![]() или
или
![]() ,
то
,
то
![]() или
или
![]() ,
т.е. выходная величина воспроизводит
входной сигнал с отставанием во времени
на время запаздывания τ.
,
т.е. выходная величина воспроизводит
входной сигнал с отставанием во времени
на время запаздывания τ.
Примеры звеньев
запаздывания можно встретить в самых
различных технологических конвейерных
установках, в системах магнитной
записи и воспроизведения, в гидравлических
системах и в электрических цепях
без потерь с распределенными
индуктивностью
![]() и ёмкостью
и ёмкостью
![]() .
.
Некоторые примеры
реальных звеньев запаздывания показаны
на рисунке 1.7.24. При загрузке сыпучего
материала на конвейер (а), движущийся
со скоростью
![]() ,
толщина слоя
,
толщина слоя
![]() ,
находящегося на расстоянии l,
отстает от толщины слоя
,
находящегося на расстоянии l,
отстает от толщины слоя
![]() ,
находящегося в начале, на время
,
находящегося в начале, на время
![]() .
Напряжение на зажимах считывающей
головки (б) магнитной системы
.
Напряжение на зажимах считывающей
головки (б) магнитной системы
![]() воспроизводит напряжение записывающей
системы
воспроизводит напряжение записывающей
системы
![]() с запаздыванием
с запаздыванием
![]() .
Напряжение
.
Напряжение
![]() в конце линии без потерь (в)
нагруженной на согласованное
сопротивление
в конце линии без потерь (в)
нагруженной на согласованное
сопротивление
![]() ,
воспроизводит напряжение в начале,
линии
,
воспроизводит напряжение в начале,
линии
![]() с запаздыванием
с запаздыванием
![]()
![]() .
.
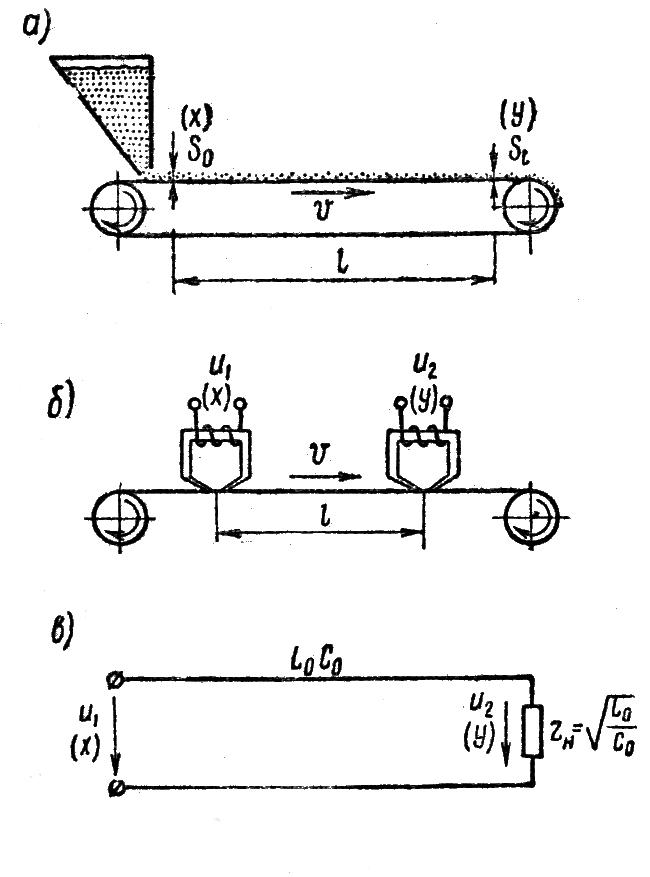
Рисунок 1.7.24 – Примеры звена запаздывания
Частотные
характеристики комплексного коэффициента
усиления, рассчитанные по формуле
(1.7.112), показаны на рисунке 1.7.25, а и
б. Амплитудно-фазовая характеристика
представляет собой окружность
единичного радиуса с центром в начале
координат (а). Окружность пересекает
вещественную ось в точке
![]() при
при
![]() и в точке
и в точке
![]() при
при
![]() .
.
Амплитудно-частотные и фазочастотные характеристики (б) определяются следующими соотношениями:
![]()
![]()
Передаточная функция звена запаздывания
![]() (1.7.113)
(1.7.113)
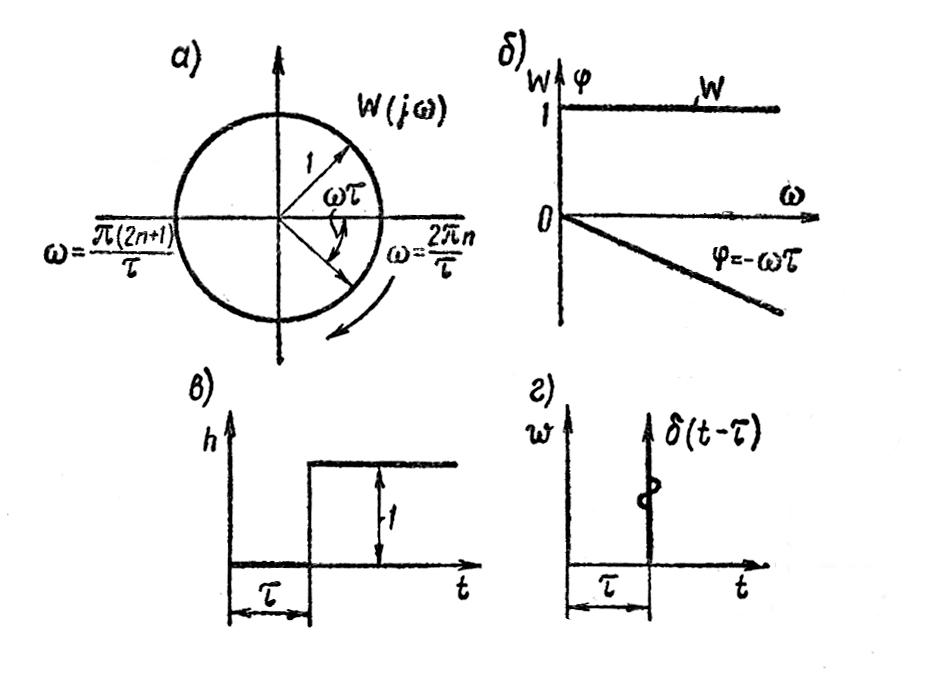
Рисунок 1.7.25 – Характеристики звена запаздывания
Звено запаздывания
является неминимально-фазовым устойчивым
звеном. Оно имеет бесконечное множество
полюсов, лежащих в левой полуплоскости,
с модулем, стремящимся к бесконечности,
и бесконечное множество нулей, лежащих
в правой полуплоскости, с модулем, также
стремящимся к бесконечности. Действительно,
уравнение
![]() имеет решение
имеет решение
![]() ,
если
,
если
![]() и
и
![]() ,
а уравнение
,
а уравнение
![]() ,
если
,
если
![]() и
и
![]() (см. рисунок 1.7.26).
(см. рисунок 1.7.26).
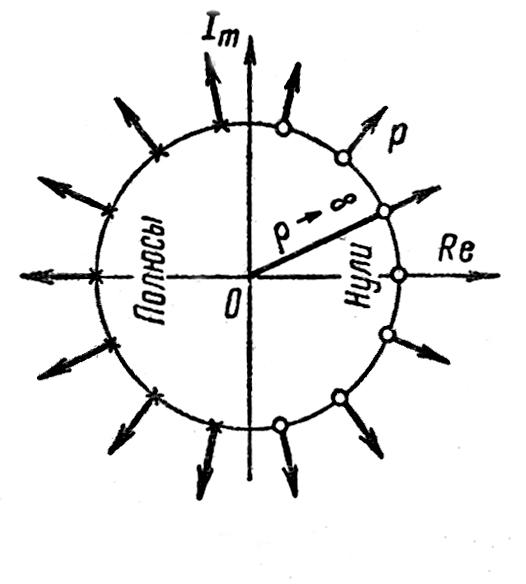
Рисунок 1.7.26 – Расположение нулей и полюсов звена запаздывания
Переходная и весовая функции (рисунок 1.7.25, в и г) имеют вид
![]() (1.7.114)
(1.7.114)
![]() (1.7.115)
(1.7.115)
Звено затухания
(или полузапаздывания). Несколько
более сложно выражаются характеристики
иррационального звена, описываемого
показательной передаточной функцией
(1.7.95). Такое звено может быть условно
названо звеном затухания, так как в
отличие от звена запаздывания в нем
сигнал на выходе всегда меньше сигнала
на входе. Оно также не является
минимально-фазовым, поскольку функция
имеет нули в правой полуплоскости при
![]() .
.
Амплитудно-фазовая характеристики звена имеет вид:
![]() (1.7.116)
(1.7.116)
На рисунке 1.7.27,
а, б построены амплитудно-фазовая,
амплитудно-частотная и фазочастотная
характеристики. Комплексный
коэффициент усиления при изменении
аргумента на
![]() уменьшается по модулю в
уменьшается по модулю в
![]() раз. Зависимость амплитуды и фазы
от частоты получается непосредственно
из (1.7.116)
раз. Зависимость амплитуды и фазы
от частоты получается непосредственно
из (1.7.116)
![]() (1.7.117)
(1.7.117)
![]() (1.7.118)
(1.7.118)
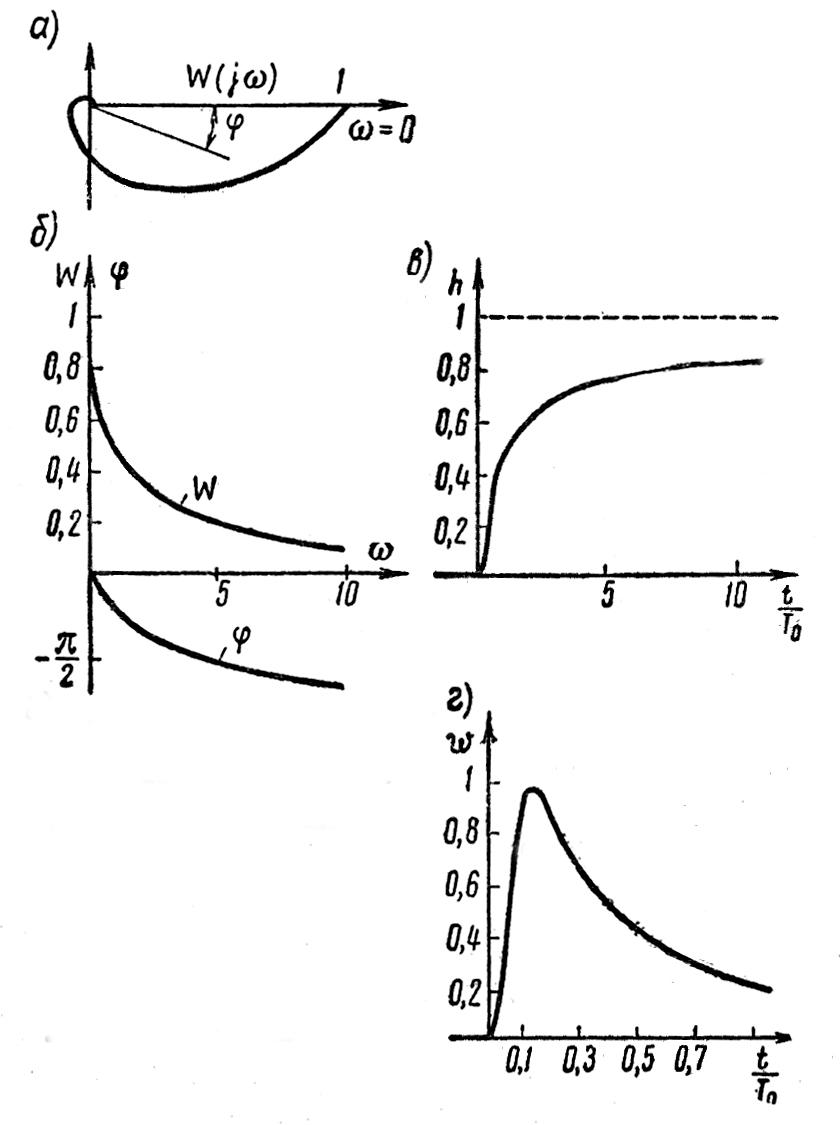
Рисунок 1.7.27 – Характеристики звена затухания
Переходная и весовая функции имеют вид
![]() (1.7.119)
(1.7.119)
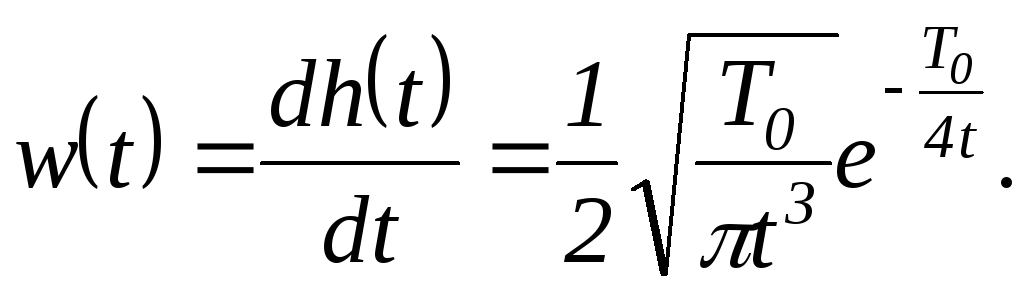 (1.7.120)
(1.7.120)
Графики этих функций показаны на рисунке 1.7.27, в и г.
