
- •Тема 1 Лінійна алгебра Системи лінійних алгебраїчних рівнянь (слар)
- •Система трьох лінійних рівнянь з трьома невідомими
- •Тема 2 Визначники другого і третього порядків та їх властивості
- •Основні властивості визначників 3-го порядку
- •Тема 3 Матриці
- •Лінійні дії над матрицями
- •Множення матриць
- •Властивості множення матриць
- •Визначник добутку матриці
- •Обернена матриця
- •Розв’язування слар матричним способом
- •Тема 2 Векторна алгебра Вектори
- •Розклад даного вектора за напрямками на прямій, на площині і в просторі
- •Лінійна залежність і лінійна незалежність системи векторів
- •Декартова прямокутна система координат
- •Лінійні операції над векторами
- •Перехід вектора до нового базису
- •Умова колінеарності двох векторів
- •Поділ відрізка у даному співвідношенні
- •Скалярний добуток векторів
- •Довжина вектора
- •Косинус кута між векторами
- •Умова ортогональності векторів
- •Проекція вектора на вектор
- •Фізичний зміст скалярного добутку
- •Векторний добуток векторів
- •Застосування векторного добутку
- •Мішаний добуток трьох векторів
- •1. Алгебрична форма комплексного числа.
- •2. Тригонометрична форма комплексного числа.
- •3. Показникові форма комплексного числа. Формули Ейлера.
- •4. Деякі застосування комплексних чисел.
- •Похідна функції
- •1. Визначення похідній, її геометричний і механічний зміст
- •Геометричний зміст похідної
- •1.2. Механічний зміст похідної
- •2. Найпростіші правила знаходження похідній
- •2.1. Похідна як функція
- •3. Похідна зворотної функції
- •4. Похідні елементарних функцій (табличні похідні)
- •5. Похідна складної функції (композиції)
- •6. Диференціал
- •6.1. Інваріантість форми диференціала
- •Геометричний зміст диференціала
- •6.3. Диференціал суми, добутку, частки
- •7. Похідні й диференціали вищих порядків
- •7.1. Неінваріантість форми диференціалів більше високого порядку
- •8. Основні теореми про диференційовані на відрізку функції
- •9. Формула тейлора і її застосування
- •Подання основних елементарних функцій по формулі тейлора
- •1. Зростання й убування функції. Екстремуми. Найбільше й найменше . Значення функції
- •1.1. Зростання й убування функції
- •2. Точки екстремуму функції
- •1.3. Найбільше й найменше значення безперервної на відрізку функції
- •2. Опуклість нагору й униз, точки перегину
- •3. Асимптоти кривих
- •4. Дослідження функцій і побудова їхніх графіків
- •5. Задачі на екстремум
Умова ортогональності векторів
Із
властивості 4 скалярного добутку випливає
умова ортогональності двох векторів:
якщо вектори
![]() і
і
![]() є ортогональними, то їх скалярний добуток
дорівнює нулю.
є ортогональними, то їх скалярний добуток
дорівнює нулю.
Якщо
![]() або якщо
або якщо
![]() (14)
(14)
Проекція вектора на вектор
![]()
![]() ,
за формулою (12) маємо
,
за формулою (12) маємо
![]() ,
звідки
,
звідки
![]() .
(15)
.
(15)
Приклад:
Трикутник
![]() заданий
координатами своїх вершин
заданий
координатами своїх вершин
![]() .
Знайти: 1) скалярний добуток векторів
.
Знайти: 1) скалярний добуток векторів
![]() ;
2) довжини сторін
;
2) довжини сторін
![]() і
і
![]() ;
3) косинус кута між стороною
;
3) косинус кута між стороною
![]() і медіаною
і медіаною
![]() .
.
Розв’язання
-
За формулою
 знайдемо координати векторів
знайдемо координати векторів
![]() .
.
За
формулою (10)
![]() знайдемо скалярний добуток векторів
знайдемо скалярний добуток векторів
![]()
![]()
![]() .
.
-
За формулою (11)
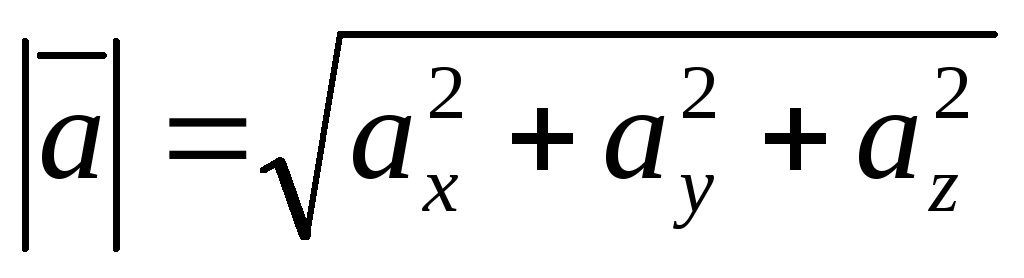 ,
знайдемо довжини сторін
,
знайдемо довжини сторін
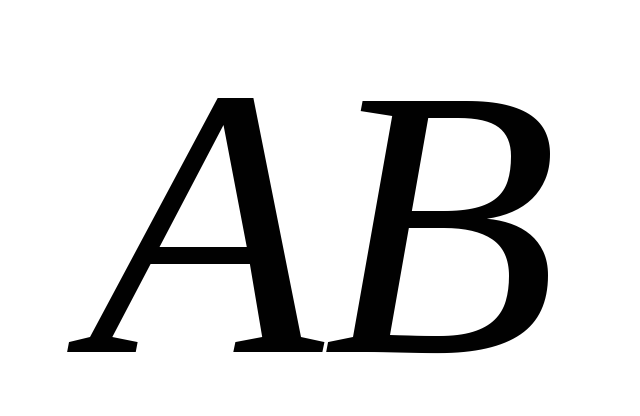 і
і
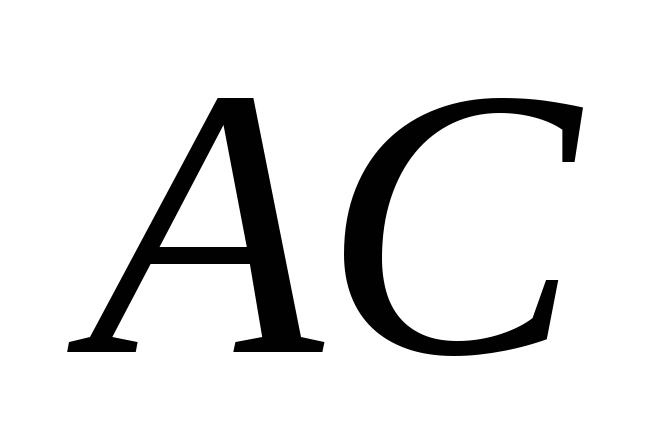
![]() .
.
-
Знайдемо координати точки
 -
середини сторони
-
середини сторони
![]()
Значить
![]() .
Тоді вектор
.
Тоді вектор
![]() має координати
має координати
![]() ,
а його довжина
,
а його довжина
![]() .
.
Тоді
косинус кута між стороною
![]() і медіаною
і медіаною
![]() визначається
за формулою (13)
визначається
за формулою (13)
![]()
Знайдемо
проекції вектора
![]() на координатні осі. Для цього розглянемо
одиничні вектори (орти)
на координатні осі. Для цього розглянемо
одиничні вектори (орти)
![]()
![]()
Як
бачимо, координати вектора
![]() є його проекціями на відповідні
координатні осі.
є його проекціями на відповідні
координатні осі.
Знайдемо
кути, які утворює вектор
![]() з осями координат (напрямні косинуси)
з осями координат (напрямні косинуси)

Напрямні
косинуси є координатами одиничного
вектора
![]() до
вектора
до
вектора
![]() .
.
![]()
![]() (16)
(16)
Приклад:
Знайти
напрямні косинуси вектора
![]() і його одиничний вектор
і його одиничний вектор
![]() .
.
Розв’язання
За формулами
![]()
знайдемо
напрямні косинуси
![]() ,
тоді
,
тоді
![]()
За
формулою
![]() знайдемо
координати одиничного вектора
знайдемо
координати одиничного вектора
![]() .
.
Можна
зробити перевірку
![]() .
.
Фізичний зміст скалярного добутку
У
фізиці робота
![]() сталої
сили
сталої
сили
![]() при прямолінійному переміщенні
матеріальної точки вздовж вектора
при прямолінійному переміщенні
матеріальної точки вздовж вектора
![]() знаходиться як скалярний добуток цих
векторів
знаходиться як скалярний добуток цих
векторів
![]() .
(17)
.
(17)
Векторний добуток векторів
Означення.
Векторним
добутком векторів
![]() і
і
![]() називається
вектор
називається
вектор
![]() ,
який задовольняє наступним умовам:
,
який задовольняє наступним умовам:
1)
![]() ,
тобто вектор
,
тобто вектор
![]() є перпендикулярним площині векторів
є перпендикулярним площині векторів
![]() і
і
![]() ;
;
2)
модуль вектора
![]() чисельно дорівнює площі паралелограма,
побудованого на векторах
чисельно дорівнює площі паралелограма,
побудованого на векторах
![]() і
і
![]() ,
тобто
,
тобто
![]() ;
;
3)
вектор
![]() направлений у той бік, з якого поворот
від
направлений у той бік, з якого поворот
від
![]() до
до
![]() на
найменший кут здійснюється проти руху
годинникової стрілки.
на
найменший кут здійснюється проти руху
годинникової стрілки.
Властивості векторного добутку
1.
![]() ;
;
2.
![]() ;
;
3)
![]() ;
;
4) Умова колінеарності векторів.
Якщо
![]() ,
тоді
,
тоді
![]() .
.
Таблиця векторного множення ортів
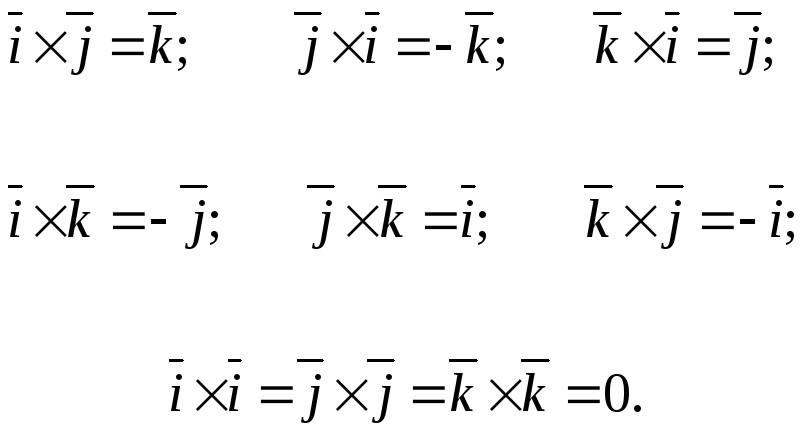
Формула векторного добутку у координатній формі
Нехай
координати векторів
![]() і
і
![]() ,
тоді
,
тоді
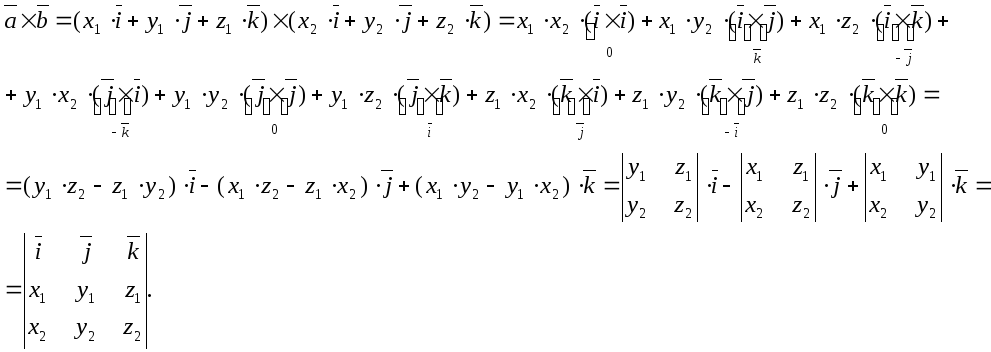
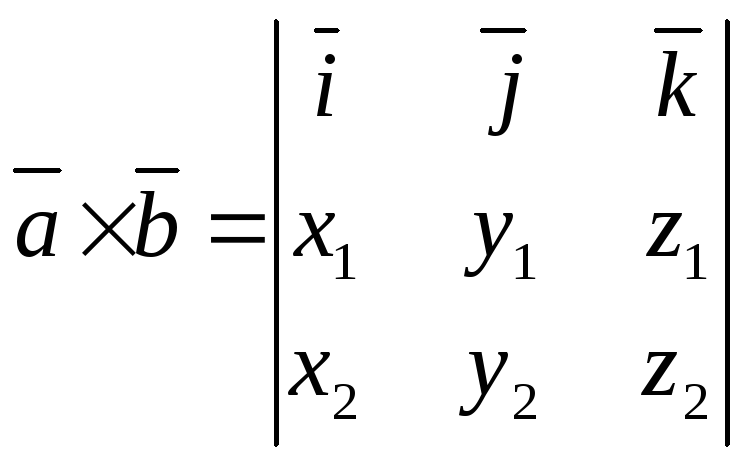 .
(18)
.
(18)
Приклад:
Знайти
векторний добуток векторів
![]() і
і
![]() та його довжину.
та його довжину.
Розв’язання
За формулою (18)
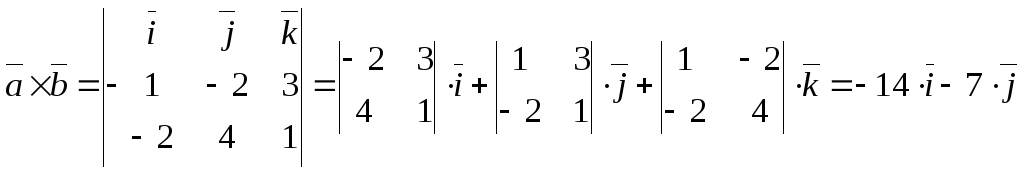 .
.
![]() .
.
