2.1. Похідна як функція

Нехай функція f визначена й диференційована в кожній точці множини X (c R), тоді в кожній точці множини X можна говорити про значення похідної функції f і тим самим на множині X визначена функція f'{х).

3. Похідна зворотної функції

ТЕОРЕМА 6. Нехай функція f:X →Y має зворотну функцію f^-1:Y→X, f диференційована в точці x₀ і f'(x_o) ≠ 0, тоді зворотна функція диференційована в точці у_о = f(х₀) і має місце формула

(10)

або

(11)

У введенні в математичний аналіз ми вже говорили, що графік зворотної функції виходить із графіка в = f(x) перетворенням симетрії відносно прямій в = х. Згадуючи геометричний зміст похідної, одержуємо (див. мал.2):

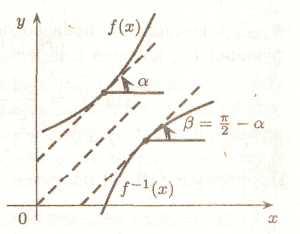
Тоді

4. Похідні елементарних функцій (табличні похідні)

У цьому параграфі ми за допомогою визначення похідній, чудових меж і теореми про похідну зворотну функцію виведемо формули для похідних елементарних функцій.

ТЕОРЕМА 7. Мають місце формули:

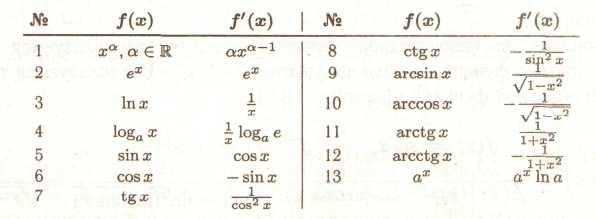
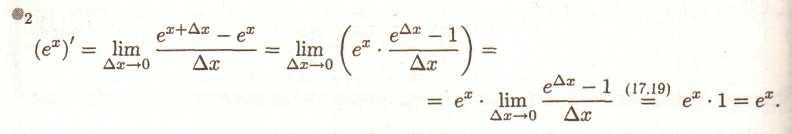
°3. Для обчислення похідної функції lnx скористаємося тим, що вона зворотня до функції е^х, що диференційована (див. °2) і її похідна не дорівнює нулю:

По формулі (11) одержуємо

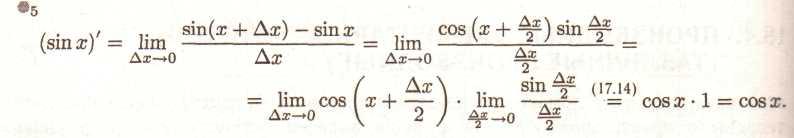
° 6. Аналогічно °5.

° 8. Аналогічно °7.

° 9. Для знаходження похідної функції arcsin х скористаємося тим, що arcsin х -зворотна функція до sinх на ділянці . Скористаємося теоремою про похідну зворотну функцію (формула (7)).

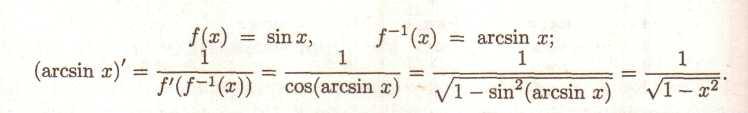
° 10. Аналогічно °9.

° 11. arctgх -функція, зворотна до тангенса на , тоді по теоремі про похідну зворотну функцію маємо

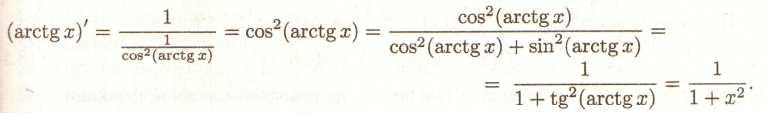
° 12. Аналогічно °11.

° 13. По теоремі про похідну зворотну функцію

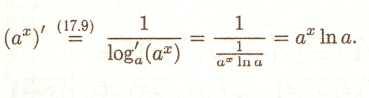
5. Похідна складної функції (композиції)

Ясно, що для обчислення похідних від елементарних функцій недостатньо теорем про похідну суму, добутку, частки й табличних похідних, тому що при утворенні функцій з основних елементарних використаються не тільки арифметичні операції, але й композиція. Зараз ми доведемо теорему про похідну складну функцію (композиції).

ТЕОРЕМА 8. Нехай f : X→Y,g: Y→Z, X,Y,Z з R і функція f диференційована в точці x₀ , а функція g диференційована в точці f(x_o), тоді композиція (складна функція) g°f : X→Y диференційована в точці x₀ і має місце формула

(12)

Ми обмежимося розглядом тільки випадку, коли g(х) монотонна в деякій околиці крапки f(х_о). Це означає, що приріст функції g в околиці крапки f₀ відмінно від нуля, коли аргументу доданий ненульовий приріст.

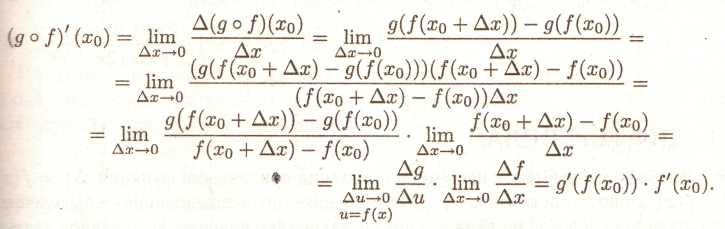
Зауваження. Складна функція може бути утворена композицією більш ніж двох функцій: F=f_n° f_n-1° °f₁, у цьому випадку потрібно представити F у вигляді F=f_n°(f_n-1° °f₁), тоді

потім по другому співмножнику застосувати той же прийом і т.д.

ПРИКЛАД 1. Знайти похідну функції

Нехай Тоді

(13)

Знайдемо и'(х) і v'(x) за допомогою теореми про похідну складну функцію.

тоді

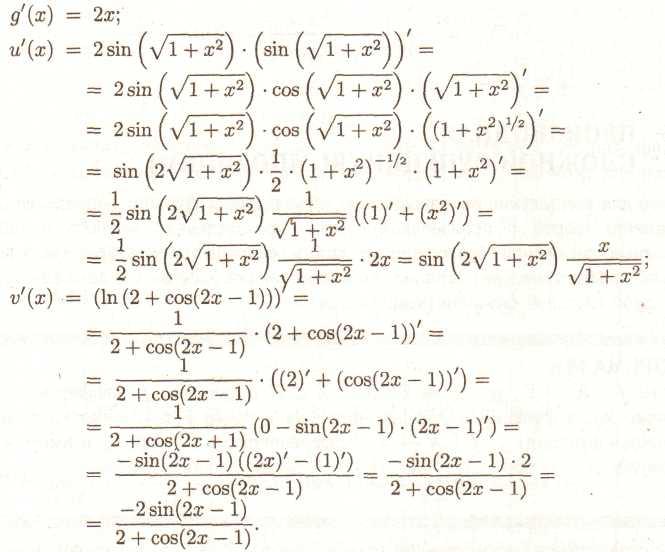
Підставляючи вираження для и'(х) і v'(x) в (18.13), одержуємо:

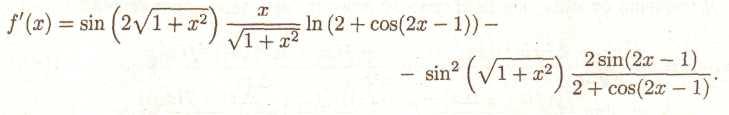
6. Диференціал

У цьому параграфі ми займемося вивченням поводження приросту функції в околиці крапки х. Головна ідея цього дослідження — виділення в головній частині (простій по конструкції) і малого (у порівнянні з головною частиною) доданка.

Якщо приріст функції вдається представити у вигляді

(14)

де Ах — постійна (певною функцією f і крапкою х), то виходить, що в околиці крапки х поводження приросту досить простої — це майже пряма пропорційна (<=> лінійна) залежність від приросту аргументу, а Ах — коефіцієнт пропорційності.

Визначення 2. Функція f(x) називається диференційованою у точці х₀, якщо приріст функції в деякій околиці крапки x₀ — s(x₀, ₀), ₀>0 можна представити у вигляді (14). При цьому головну (лінійну) частина приросту називають диференціалом функції f/ і позначають df, тобто

(15)

Помітимо, що до цього диференційованою у точці х_о ми називали функцію, що має похідну в точці х_о. Це не випадково. Виявляється (і в цьому зміст наступної теореми), що подання приросту функції у вигляді (14) можливо тоді й тільки тоді, коли функція має похідну в точці х_о, більше того, А_Хо =f'(x_о).

ТЕОРЕМА 9. Функція f диференційована в змісті визначення (2) тоді й тільки тоді, коли функція f має похідну в точці x₀, при цьому

(16)

т. е. для А_Хо в (14) має місце рівність

при цьому (14) має вигляд

Після того як ми дали визначення похідній (1), було показано, що якщо функція має похідну, то в деякої ₀ -околиці ₀ >0 крапки х_о має місце рівність (1)

а це й означає, що має місце диференційованість у змісті визначення 2 і

Покажемо тепер, що якщо функція f диференційована в змісті визначення 2, то вона має похідну в точці х₀ і f (x₀) = A_XQ.

Нехай , тоді

(17)

З рівності (17) треба

Значення уведеного поняття й установлення його зв'язку з похідній важко

переоцінити.

Розглянемо зараз, не обґрунтовуючи строго, застосування диференціала до наближених обчислень

Отже, , виходить,

ПРИКЛАД 2. Обчислити приблизно .

Розглянемо функцію f(x) = . У якості х_о візьмемо 25, тоді =—0,11.

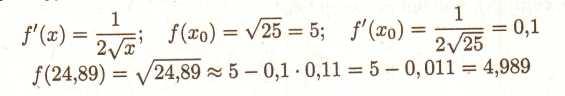
(помітимо, що наближене значення з точністю до 9-го знака після коми таке: 4,988987873).