Застосування векторного добутку

1.Момент сили відносно точки.

Якщо сила прикладена до точки , тоді момент цієї сили відносно точки дорівнює векторному добутку векторів (важіль) і .

. (19)

Приклад: Сила прикладена до точки . Знайти момент сили відносно точки .

Розв’язання

Важіль .

2. Площа паралелограма, побудованого на векторах, площа трикутника.

За означенням векторного добутку, площа паралелограма, побудованого на векторах і , дорівнює модулю векторного добутку к, а площа трикутника .

Приклад: Знайти площу трикутника, з вершинами .

Розв’язання

.

.

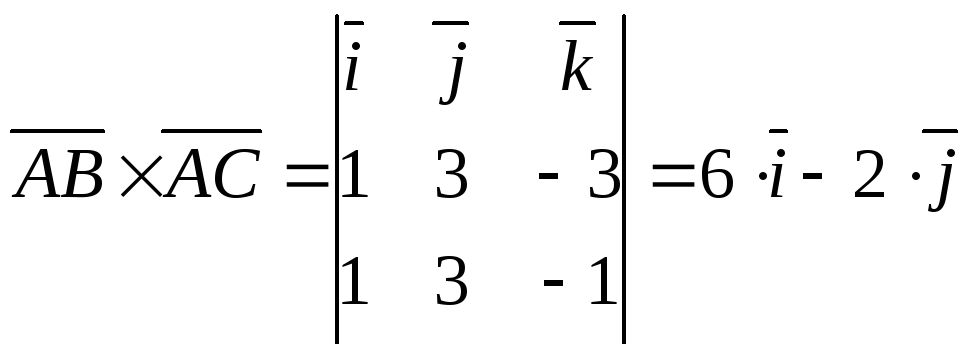Мішаний добуток трьох векторів

Означення: Мішаним (векторно-скалярним) добутком трьох векторів , і називається скалярна величина, що дорівнює скалярному добутку вектора на вектор .

Мішаний добуток у координатній формі

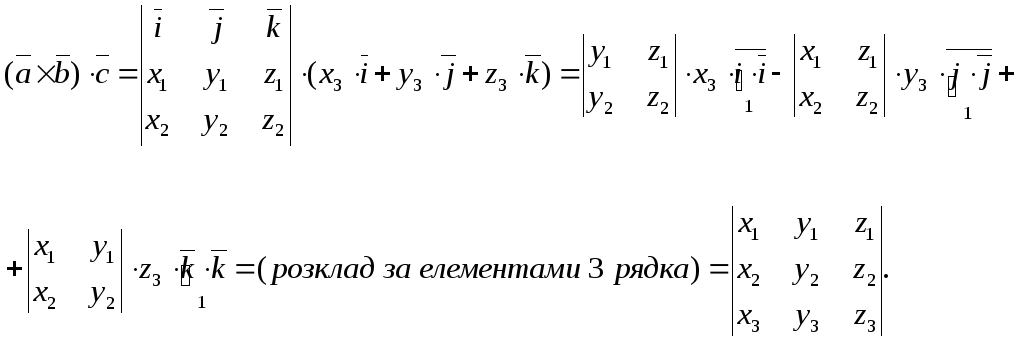
Отже (20)

Властивості мішаного добутку векторів

1. Вектори , і компланарні тоді і тільки тоді, коли їх мішаний добуток дорівнює нулю (умова компланарності векторів).

або .

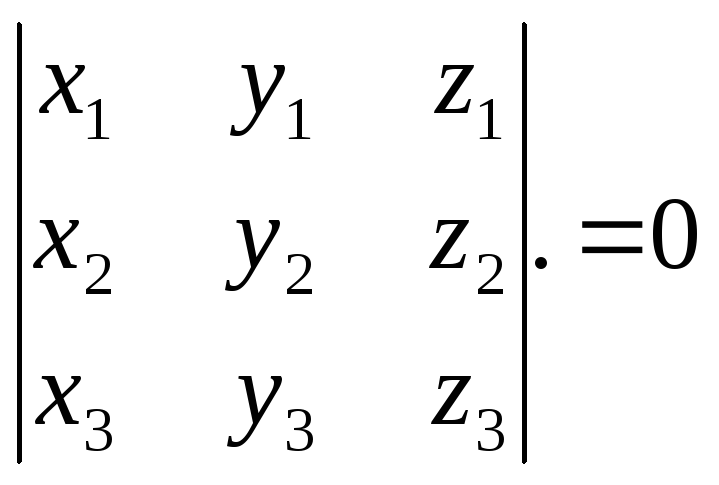2.

3.

Приклад: Довести, що точки лежать в одній площині.

Розв’язання

Знайдемо координати векторів

Значить вектори є компланарними, тобто лежать в одній площині.

Геометричний зміст мішаного добутку

Об’єм паралелепіпеда, побудованого на векторах , і , зведених до однієї точки О , дорівнює модулю мішаного добутку цих векторів.

. (21)

Відповідно об’єм піраміди, побудованої на векторах , і , дорівнює об’єму піраміди

. (22)

Приклад: Знайти об’єм піраміди, вершинами якої є точки з координатами .

Розв’язання

Зведемо вектори, що утворюють піраміду, до однієї точки, наприклад А і знайдемо їх координати

Знайдемо мішаний добуток векторів

За формулою (22), об’єм піраміди дорівнює

Комплексні числа

1. Алгебрична форма комплексного числа.

2. Тригонометрична форма комплексного числа.

3. Показникові форма комплексного числа. Формули Ейлера.

4. Деякі застосування комплексних чисел.

1. Алгебрична форма комплексного числа.

Комплексним числом (КЧ) називається пара дійсних чисел a і b, записаних у вигляді z = a + bi, де число i – так звана уявна одиниця: i² = - 1, тобто .

Необхідність виконувати дії із розв’язками рівняння x² + 1 = 0 призвела до введення нових операцій, і до поняття КЧ. Запис z = a + bi називають алгебричною (алгебраїчною) формою КЧ z. Число a називають дійсною частиною числа z, а b – уявною частиною. Позначають a = Re z, b = Im z. Якщо a = 0, то число 0 + bi = bi називається суто уявним. У випадку b = 0 дістанемо дійсне число: a + 0i = a. Два комплексні числа z = a + bi та , які відрізняються лише знаком явної частини, називаються спряженими.

Два КЧ z₁ = a₁ + b₁i і z₂ = a₂ + b₂i називаються рівними тоді і тільки тоді, коли a₁ = a₂ і b₁ = b₂, тобто тільки тоді, коли рівні їхні відповідно дійсні та уявні частини.

Додавання та віднімання КЧ здійснюють за такими правилами:

z₁ + z₂ = (a₁ + a₂) + (b₁ + b₂)i, z₁ - z₂ = (a₁ - a₂) + (b₁ - b₂)i.

Д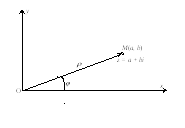ля множення комплексних чисел z₁ = a₁ + b₁i і z₂ = a₂ + b₂i використаємо рівність i² = - 1, виконуючи множення за звичними правилами:

z₁z₂ = (a₁ + b₁i)(a₂ + b₂i) = a₁a₂ + a₁b₂i ++ b₁a₂i + b₁b₂i² = 

= (a₁a₂ - b₁b₂) + (a₁b₂ + b₁a₂)i

Для виконання операції ділення зауважимо, що добуток є дійсним числом. Тому помноживши чисельник і знаменник частки на число, спряжене знаменнику, дістанемо результат ділення: