7.1. Неінваріантість форми диференціалів більше високого порядку

Помітимо, що властивість інваріантості форми диференціала 1-го порядку для диференціалів більше високого порядку не спостерігається. Покажемо це на прикладі диференціала другого порядку. Розглянемо два випадки:

а) f(x), х — незалежна змінна;

б) f(x), x = φ(t), t — незалежна змінна. Ясно, що у випадку а) ми маємо

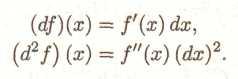
У випадку б)

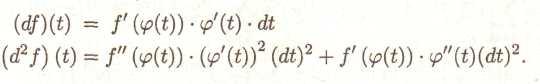
Якщо в останнім вираженні повернутися до того, що х = φ(t), той перший доданок може бути записане у вигляді f"*(dx)², а наявність що складає f'(φ(t))φ"(t)(dt)² і означає втрату інваріантості форми 2-го диференціала.

8. Основні теореми про диференційовані на відрізку функції

Зараз будуть доведені три основні теореми про диференційовані на відрізку функції, що задовольняють деяким додатковим умовам. Потім, застосовуючи ці теореми, ми одержимо нові потужні способи обчислення меж у ситуаціях, коли ми маємо справу з основними невизначеностями виду й .

ТЕОРЕМА 14 (Теорема Ролля)

Нехай функція f визначена й безперервна на відрізку[а,b], а <b диференційована на (а,b) і f(а)= f (b), тоді існує точка _x0 € (а, b) така, що

Ми вже знаємо що функція, безперервна на відрізку [а,b], досягає на ньому свого найбільшого й найменшого значення, тобто існують х_т, х_М € [а,b] такі, що

(32),

(32),

Можливі два випадки:

а). З нерівностей (32) і (33) треба, що f (x) - постійна на відрізку [а,b] функція, тоді f'(x)=0 у всіх точках інтервалу (а,b) і твердження теореми виконане.

б). У цьому випадку: 1) функція f не постійна; 2) принаймні одна із крапок х_т, хм належить інтервалу (а,b).

Розглянемо випадок, коли х_М € [а,b] і покажемо, що f'(х_М) = 0.

Дійсно, тому що х_М — точка максимуму, те, якщо х > 0, те

тоді

(34)

а якщо х < 0

але тоді

(35)

З (34) і (35) треба, що f'(х_М) = 0.

Визначення 3. Нехай f : X → Y, X, Y З R, точка x₀ € X називається крапкою локального максимуму (мінімуму), якщо існує δ₀ > 0 таке, що s(x₀, δ₀₎ € X і для всіх крапок х з s(x₀, δ₀₎ виконана нерівність

Крапки локального максимуму або мінімуму називають точками локального екстремуму.

Справедлива наступна теорема про необхідну умову локального екстремуму диференційованою функції:

ТЕОРЕМА 15 (Теорема Ферма)

Якщо функція f диференційована в точці x₀ і точка x₀ є крапкою локального екстремуму, то f'(x₀) = 0.

• Доказ теореми аналогічно доказу того, що f'(х_М) = 0. у випадку б) теореми 28.

Зауваження. З теореми Ферма треба, що точками, «підозрілими» на екстремум, є крапки звернення до нуля похідної й крапки, у яких похідна не існує.

ТЕОРЕМА 16 (Теорема Лагранжа)

Нехай функція f(х) безперервна на [а,b] і диференційована на [а,b], тоді існує точка х₁ € (а,b) така, що

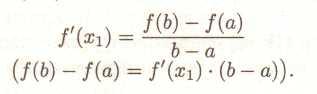(38)

П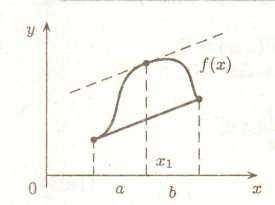ерш ніж доводити теорему Лагранжа, зупинимося на її геометричному змісті. Вираження, що коштує в правій частині рівності (38),— кутовий коефіцієнт хорди, проведеної через крапки графіка функції f з абсцисами а й b (хорда, що стягає графік на ділянці [а,b], див. мал. 4.

Виходить, у теоремі Лагранжа затверджується, що існує така точка (х₁,f(x₁)), що дотична до графіка функції в цій точці паралельна стягуючій хорді.

• Побудуємо по функції f допоміжну функцію f₁ так, щоб вона задовольняла умовам теореми Ролля. Покладемо

(39)

Ясно, що

1) f₁(a) = f₁(b) = f(a);

2) f₁ безперервна на [а,b] і f₁ диференційована на (а,b). Тоді, по теоремі Ролля, існує точка х₁ € (а,b), у якій

(40)

Обчислимо f'₁(х)

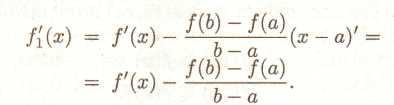(41)

З (40) і (41) одержуємо, що

Зауваження. З мал. 4 видно, що точка, що задовольняє теоремі Лагранжа, може бути не одна.

ТЕОРЕМА 17 (Теорема Коші)

Якщо функції f(x) і g(х) безперервні на [а,b] , диференційовані на (а,b) і g'(х) не звертається в нуль у жодній точці інтервалу (а,b), тоді існує точка х₂ € (а,b) така, що

Розглянемо функцію

(42)

Ясно, що функція f₂(x) задовольняє умовам теореми Ролля (f₂(а)=f₂(b)=0) тоді існує точка х₂ € (а,b) така, що

(43)

Обчислимо f₂(x):

(44)

З (43) і (44) треба, що

ТЕОРЕМА 18 (Правило Лопиталя)

Нехай

1) функції f(x) і g(х) визначені в деякій околиці крапки х_о й f(x₀)= g(x₀)=0;

2) f(x) і g(х) диференційовані в точці х_о й g'(х_о)≠0 Тоді існує й

(45)

Умови теореми 30 можуть бути трохи ослаблені.

Теорема 18' Нехай

1. функції f(x) і д(х) визначені в деякої виколотої δ_{o-околиці}, δ_o>0 крапки х₀ s'(x_o,δ_o) і ;

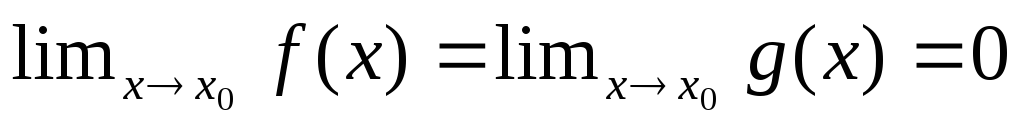2. f(x) і g(x) диференційовані у виколотій околиці крапки х₀ — s'(x₀, δ_o)і g'(х) не звертається в нуль у жодній точці s'(x₀, δ_o);

3) існує (кінцевий або нескінченний) . Тоді існує й має місце рівність:

(46)

Зауваження. Зверніть увагу на відмінність рівності (46) від (45).

Рівність (46) залишає більшу свободу дій, а саме, якщо f’ b g’ такі, що вони самі задовольняють умовам теореми 18.18', те

Таким чином, при рішенні прикладів іноді доводиться застосовувати правили Лопіталя (теорему 18') кілька разів (доти, поки не відбудеться розкриття невизначеності).

ТЕОРЕМА 19 (Друге правило Лопіталя)

Нехай

1). функції f(x) і д(х) визначені в деякої виколотої δ_{o-околиці}, δ_o>0 крапки х₀ s'(x_o,δ_o) і ;

2). f(x) і g(x) диференційовані у виколотій околиці крапки х₀ — s'(x₀, δ_o)і g'(х) не звертається в нуль у жодній точці s'(x₀, δ_o);

3). існує (кінцевий або нескінченний) . Тоді існує й має місце рівність (46), тобто:

Зауваження. До другого правила Лопіталя можна зробити таке ж зауваження, як і до теореми 18.18'.

ПРИКЛАД 5. Обчислити

Ясно, що ми перебуваємо в умовах теореми 18.18'. Застосуємо правило Лопіталя