Похідна функції

1. Визначення похідній, її геометричний і механічний зміст

У цій лекції ми вертаємося до знайомого зі шкільної математики поняттю похідної функції, її геометричному й механічному змісту, найпростішим правилам знаходження похідній.

Визначення 1. Нехай f : X→Y, X, Y з R, х₀ ЄX і існує δ₀ > 0 таке, що s(x₀, δ₀₎ З X. Похідної функції f у точці х₀ називається

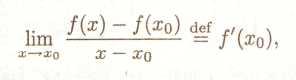(1)

якщо ця межа існує, і в цьому випадку говорять, що функція f диференційована в точці х₀; якщо ж межа в (1) не існує, то говорять, що функція f(x) не диференційована в точці x₀.

Зауваження. Якщо позначити, то (1) у цих позначеннях

прийме вид (2)

ТЕОРЕМА 1. Якщо функція f диференційована в точці x₀ , то вона в цій точці

безперервна.

Рівність означає

а) якщо є нескінченно малої, того ж

порядку, що й

б) якщо є нескінченно малої, більше високого порядку, що

і

Але так чи інакше, ∆f є нескінченно малою при ∆х→ 0. Це означає (по визначенню нескінченно малої), що

Останнє рывно тому, що

Отже, функція f(x) неперервна в точці x_0.

Зауваження. Рівність означає що прагне до 0 при ∆х→ 0. Тоді

Останній перехід зроблений з обліком того, що

Ми одержали формулу (3)

або (4)

1. Геометричний зміст похідної

Розглянемо графік функції в = f(x), X,Y Є R. Згадаємо визначення дотичної до кривої, дане в розділі «Алгебра й геометрія». Зафіксуємо на графіку функції дві крапки М₀(х₀,f(х₀)) і M₁(х₀+∆х,f(х₀+∆х)) і знайдемо кутовий коефіцієнт січної, минаючої через ці крапки. Ясно, що він обчислюється по формулі (cм. мал. 1)

Якщо існує граничне положення січної, коли ∆х→ 0, те отримана пряма називається дотичній до графіка в = f(x) у точці х₀. Зрозуміло, що умовою існування граничного положення січної є існування наступної межі

Ми вже довели, що графік функції в = f(x) має дотичну в точці х_о тоді й тільки тоді, коли функція диференційована в точці х_о й f'(х_о) є кутовим коефіцієнтом дотичної.

Складемо тепер рівняння дотичної в точці х_о, як рівняння прямої, що проходить через крапку M_o(x_o, f(x_o)) і має кутовий коефіцієнт, рівний f'(х_о):

(5)

1.2. Механічний зміст похідної

Розглянемо рух матеріальної крапки. Допустимо, відомий закон s(t) зміни 1 відстані від крапки, що рухається, до деякої фіксованої крапки залежно від часу t, t ЄТ. Середня швидкість крапки на тимчасовому відрізку [t_о,t_о + ∆t] виражається формулою

Миттєвою швидкістю крапки в момент часу t_o називають величину v(t_o), певну рівністю

Згадуючи визначення похідної, одержуємо, що

т. е. миттєва швидкість крапки, що рухається, v(to) - це похідна за часом закону руху.

2. Найпростіші правила знаходження похідній

ТЕОРЕМА 2. Похідна постійної дорівнює 0, тобто (З)' = 0.

Очевидно, це вірно, тому що ?З = 0.

ТЕОРЕМА 3. Нехай fug диференційовані в точці х₀, тоді f+g диференційована в точці х_о й має місце формула

(6)

Знайдемо

тоді

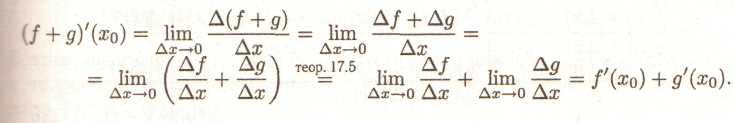
ТЕОРЕМА 4. Нехай f та диференційовані в точці х₀, тоді f*g диференційована в точці х_о й має місце формула

(7)

Знайдемо

Тоді

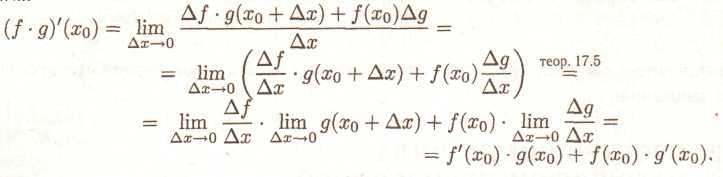
Зауваження. тому що за умовою теореми функція g диференційована в точці х₀, і виходить, (теорема 1) безперервна.

Наслідок з теореми 4. Для будь-якого а € R має місце формула

(8)

ТЕОРЕМА 5. Нехай f(x) і g(х) диференційовані в точці х₀ і тоді функція диференційована в точці x₀ і має місце формула

(9)

Знайдемо